李宏毅机器学习任务四

贝叶斯公式

$P(C_i|x)=\frac{P(x|C_i)P(C_i)}{{\sum }_{i=1}^{c}P(x|C_i)P(C_i)}$
x为一个样本，是一个特征向量 C为所有类别的集合 $C_i$为第$i$类。

后验概率

在给定样本X时，计算它属于$C_i$类的概率，实际上就是条件概率。
由似然函数和先验概率分布相乘并除以归一化常数

先验概率

$P(C_i)$ i=1,2,…k
是估计$C_i$类在模型中的概率

贝叶斯估计最大似然函数估计的区别

贝叶斯估计引入了先验概率，通过先验概率和似然概率来求解后验概率。而最大似然估计是直接通过最大化似然概率来求得
引入一个例子：
男性中30%留长头发，女性中60%留长头发。现在看到一个留长头发的人，判断他的性别。
1.使用最大似然估计,$max(P(长头发|男生)，P(长头发|女生))$，则推断这个人是女生
2.使用贝叶斯估计，这里要引入先验概率，男性占比90%，女性占比10%
则
$P(男生|长头发)=\frac{P(长头发|男生)P(男生)}{P(长头发)}=\frac{0.27}{P(长头发)}$
$P(女生|长头发)=\frac{P(长头发|女生)P(女生)}{P(长头发)}=\frac{0.06}{P(长头发)}$
是男生的概率大，推断这个人是男生

朴素贝叶斯算法

朴素贝叶斯算法是利用贝叶斯公式推断样本x分别属于类别$C_i$的概率，选出概率最大的那一类，将样本分为此类。
朴素贝叶斯通过训练数据集学习联合概率分布$P(X,C_i)$，对条件概率分布作了条件独立的假设$P(x|C_i)={\prod }_{n=1}^{N}P(x_n|C_i)$，属于生成模型算法 ，是根据联合概率分布，确定后验概率。
样本x是一个向量，特征维为N。
$类别=argma{x}_{c_i}=P(C_i)\prod P(x_n|C_i)$

当特征值为离散的时候

用出现的次数估计条件概率和先验概率

当特征值为连续的时候

1.通常假设这些连续数值为高斯分布，用高斯分布可以将在类别$C_i$的条件下x的 均值和方差计算出来。
2.大量样本情况下，通过离散化连续值的方法。在训练本较少或者精确的已知分布时，通过概率分布的方法是一个好的选择

推导sigmoid function

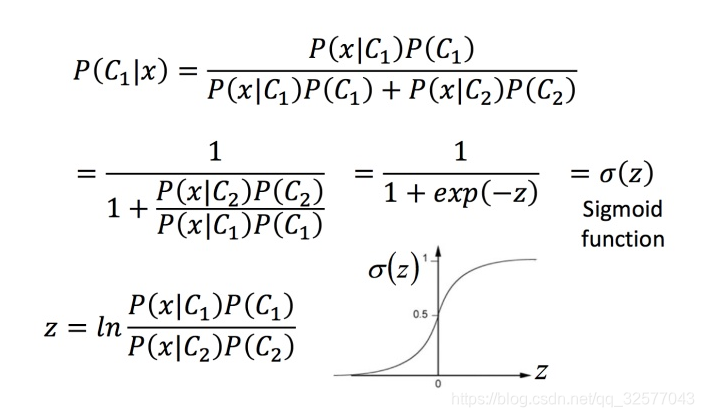
由上面的推导可以得到

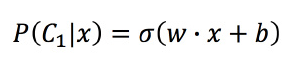
逻辑回归和线性回归的关系

相同之处：

1. 都是通过极大似然估计对训练样本建模
   线性回归：假设因变量y服从正态分布的假设，用极大似然估计去选择超参$w$
   逻辑回归：通过对数似然函数去选择超参$w$
2. 在超参求解过程中，都可以利用梯度下降

不同之处:

1. 逻辑回归处理分类问题，线性回归处理回归问题
2. 逻辑回归中类别是因变量服从二项分布，线性回归中y是自变量，假设服从高斯分布
   .