2019CS224N-01

机器学习与深度学习介绍

深度学习是机器学习的一个分支。
传统机器学习都是围绕着决策树、逻辑回归、朴素贝叶斯、支持向量机（SVM）等概念，由人类审视一个特定的问题，找出解决问题的关键要素，设计出与该问题相关的重要特征要素，然后手写代码。人们根据确定的要求会不断加入新的特征，最终系统会有数百万个人工设定的特征。人类去研究如何描述数据，总结出重要特征，只有10%的工作是电脑进行这一数值优化算法。
深度学习是表征学习的一个分支，表征学习的理念是，我们可以只向电脑提供来自世界的原始信号（视觉、语言、其他），然后电脑可以得出好的中介表征来很好的完成任务，即让计算机自己定义特征，和机器学习通过人类来定义特征是一样的。DL将学到多层的学习表征。
简而言之，ML是人类尽可能指定所有可能的特征，DL是自己去定义特征硬练。

人类语言和词义

人们通过语言进行知识传播，我们拥有人类计算机网络，我们使用人类语言作为我们的网络语言以实现人类计算机网络。

1. 我们使用wordnet在计算机中拥有可用的意思（一个包含同义词集和超常词列表的同义词典）
   e.g. good的同义词集合

import nltk
from nltk.corpus import wordnet as wn

nltk.download('wordnet')
poses = { 'n':'noun', 'v':'verb', 's':'adj (s)', 'a':'adj', 'r':'adv'}
for synset in wn.synsets("good"):
    print("{}: {}".format(poses[synset.pos()], ", ".join([l.name() for l in synset.lemmas()])))

noun: good
noun: good, goodness
noun: good, goodness
noun: commodity, trade_good, good
adj: good
adj (s): full, good
adj: good
adj (s): estimable, good, honorable, respectable
adj (s): beneficial, good
adj (s): good
……
adv: well, good
adv: thoroughly, soundly, good

• 类似于WordNet的资源会存在这些问题：
  • 作为一个资源很好，但缺少细微差别
    如：“proficient”被列为“good”的同义词。但是这仅仅在某些语境下是成立的。
  • 缺少单词的新含义
    如：wicked, badass, nifty, wizard, genius, ninja, bombest
  • 不能与时俱进
  • 主观性
  • 需要人为来创造和适应
  • 无法计算准确的单词相似性
• 使用one-hot向量来表示单词
  在传统的自然语言处理中，我们把词语看作离散的符号
  
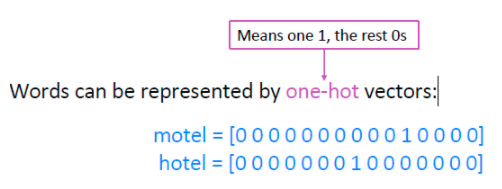
  这也会存在一些问题，比如我们搜索Seattle motel，我们同时还会得到Seattle hotel，hotel和motel几乎上是同一个东西；如果我们使用one-hot向量，那么这两个词是正交的没有相似关系。
• 解决方案
  我们引入分布语义学，我们通过观察上下文来表示单词的含义。
  比如：我们要知道bank的意思，抓取了很多文本，获取使用bank的上下文，这样可以很好的抓取该单词的意义

Word2vec

• Word2vec是具有分布式的单词表示形式。我们把词的含义作为一个神经词向量，这样我们可以实现意义的可视化。
  下图展示了一个词对应的向量以及投影到二维空间的表示：
  

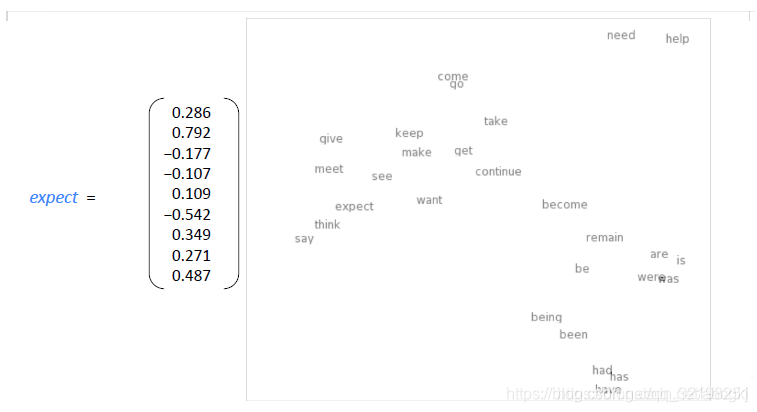
• 过程详解
  Word2vec是一种从原始文本中学习嵌入词的高效预测模型。它有两种方法：连续的词袋模型(CBOW)和跳格模型(skip-gram)。从算法上来说，这些模型是相似的，CBOW从源上下文词预测目标词，而skip-gram则相反，从目标词预测源上下文词。
  这里理解课程推导的内容使用了skip-gram方法就更好理解了。
  每个词我们都由一个向量表示，其中我们定义文本当中当前词的位置序列是t(target)，中心词是c(center)，上下文词是o(outside)。用向量c和o的相似度（比如说余弦相似度）来计算给定c到o的概率。我们期待的情况是，这个概率可以达到最大化。
  对于每个位置t= 1，…，T，预测一个固定大小为m的窗口、中心词为 $w_t$，预测context words：
  $$Likehood=L(\theta )=\prod _{t=1}^T\prod _{-m\le j\le m,j\ne 1}P({\omega }_{t+j}|{\omega }_t,\theta )$$
  objective function是likehood的平均负log（average negative log likehood），我们想要得到目标函数的最小值:
  $$objectivefunction=J(\theta )=-\frac{1}{T}logL(\theta )$$$$=-\frac{1}{T}\sum _{t=1}^T\sum _{-m\le j\le m,j\ne 1}P({\omega }_{t+j}|{\omega }_t,\theta )$$
  其中，objective function有时也被称作loss function或者cost function；$\theta$是是所有要被优化的变量；目标函数是对似然函数进行log，这样累乘可以变成累加，前面又加了一个负号，又乘1/T进行平均，由最大值改为求最小值。
  根据上面的算式推到，我们的目标是通过训练模型，也就是改变参数θ的值，来最小化 $J(\theta )$，也就是为了求得P的最小值，对于每个单词w，我们将使用两个向量：

  • $v_w$:当w是中心词的时候，$v_w$代表中心词向量，维度设为d维（本课程中设为100维特征，现google最新已为300维），故对于中心词c，对应的词向量为$v_c$
  • $u_w$ :当w是上下文词的时，$u_w$代表上文词向量，维度设为d维，故对于上下文词o，对应的词向量为$u_o$
  • 一共用V个词汇
    我们要求$P({\omega }_{t+j}|{\omega }_t)$的最小值，相当于计算对于中心词c和上下文词o时的概率，即：
    $$P(o|c)=\frac{exp(u_o^T{v}_c)}{{\sum }_{w\in V}exp(u_w^T{v}_c)}$$
    两个单词越相似，点积结果越大。(A·B=|A||B|cos$\theta$)
    这里计算logP对$v_c$的偏导数，用向量表示所有的参数，有V个单词，d维向量。每个单词有2个向量。参数个数一共是2dV个。
    $$\frac{\partial }{\partial v_c}logP(o|c)=\frac{\partial }{\partial v_c}log\frac{exp(u_o^T\cdot v_c)}{{\sum }_{w=1}^{V}exp(u_w^T\cdot v_c)}=\underset{1}{\underbrace{\frac{\partial }{\partial v_c}logexp(u_o^T\cdot v_c)}}-\underset{2}{\underbrace{\frac{\partial }{\partial v_c}log\sum _{w=1}^{V}exp(u_w^T\cdot v_c)}}$$
    式子1我们可以得到其倒数为$u_o$;
    式子2的推导过程如下：
    
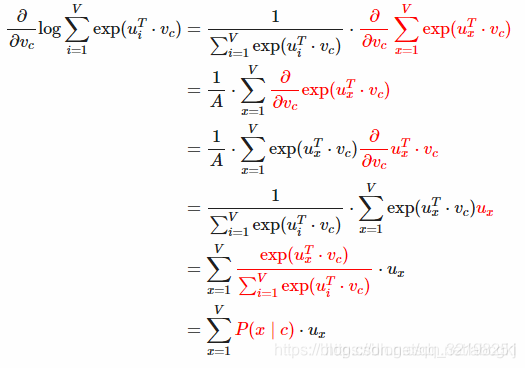
    注：公式中的x为避免和前面的i重复。
    所以，综合起来可以求得，单词o是单词c的上下文概率
    logP(o∣c)，对center向量$v_c$
    
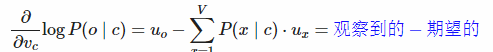
    实际上偏导是，单词o的上下文词向量，减去，所有单词x的上下文向量乘以x作为c的上下文向量的概率。

• 总体梯度计算:
  在一个window里面，对中间词汇$v_c$
  求了梯度， 然后再对各个上下文词汇$u_o$
  求梯度（本文中没有写，感兴趣可自行计算）。然后更新这个window里面用到的参数。
  通常在每个窗口中，我们将计算该窗口中使用的所有参数的更新。例如：
  

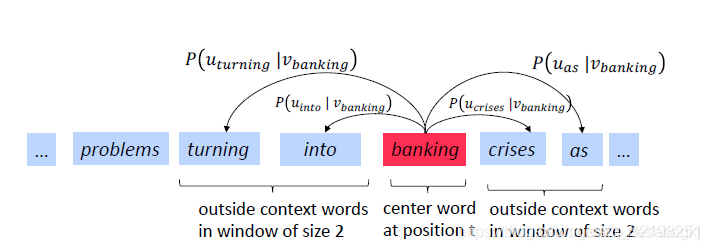
• 梯度下降
  有了梯度之后，参数减去梯度，就可以朝着最小的方向走了。机器学习梯度下降
  
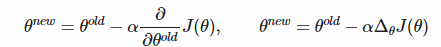
  -优化梯度

1. 方法
   我们最小化目标函数：J ( θ ) J(\theta)J(θ)
   梯度下降是一种最小化J ( θ ) J(\theta)J(θ)的算法
   思想：对于当前θ值，计算J ( θ ) J(\theta)J(θ)的值，然后在负梯度的方向上迈步
   

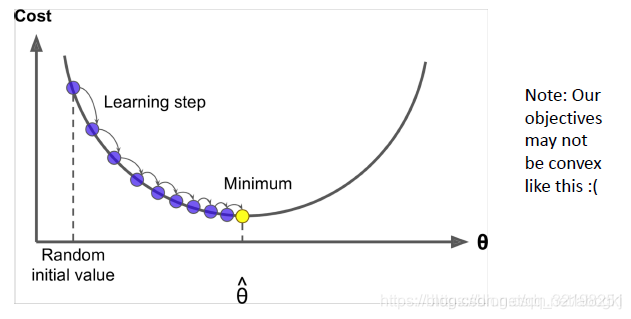
2. 具体细节
   更新方程（以矩阵表示）
   
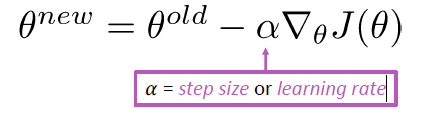
   更新方程（对于单个参数）
   
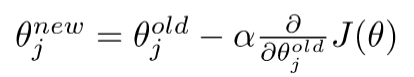
   算法：
   

3. 随机梯度下降
   问题：J ( θ ) J(\theta)J(θ)是语料库中所有窗口的函数（数以亿计），所以计算J(θ)的梯度非常耗费资源，您需要等待很长时间才能进行一次更新，对于几乎所有的神经网络来说，这是一个非常糟糕的方法。
   解决方法：随机梯度下降（Stochastic gradient descent，SGD），即重复示例窗口，并在每个窗口之后更新
   随机梯度下降算法：