堆、堆排序与优先队列

最新推荐文章于 2025-04-24 17:46:29 发布

Maricat4

最新推荐文章于 2025-04-24 17:46:29 发布

阅读量169

点赞数 1

分类专栏：经典算法文章标签：算法数据结构

本文链接：https://blog.youkuaiyun.com/qq_32061629/article/details/105773077

版权

经典算法专栏收录该内容

9 篇文章

订阅专栏

堆、堆排序与优先队列

堆(heap)

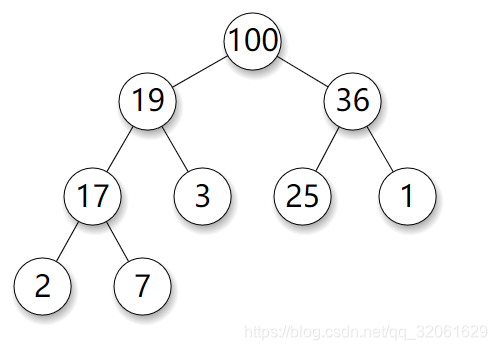
堆(Heap)是计算机科学中一类特殊的数据结构。堆通常用数组来实现。把堆近似看作一棵完全二叉树（最底层可能不是完全填满的，如下图），堆中结点的值总是不大于或不小于其父结点的值。
根结点最大的堆叫做最大堆或大根堆。
根结点最小的堆叫做最小堆或小根堆。

最小堆示例：

在这里插入图片描述

表示堆的数组 $A$ 有两个属性： $A . l e n g t h$ 表示数组元素的个数， $A.heap\_size$ 表示有多少个堆元素存储在数组中。有 $0\le A.heap\_size\le A.length$ 。树的根节点是 $A [1]$ 。
给定一个节点的下标 $i$ 那么它的父节点，左孩子和右孩子的下标：
$\llcorner i/2\lrcorner,LEFT(i)=2i,RIGHT(i)=2i+1$

这是对于首元素为 $A [1]$ 而言的，如若是 $A [0]$ ，相似地，为：
$\llcorner (i-1)/2\lrcorner,LEFT(i)=2i+1,RIGHT(i)=2(i+1)$

堆有关操作（以最小堆为例）

维护堆
建堆

维护堆

这是用于维护堆的性质的过程。它的输入为一个数组 $A$ 和一个下标 $i$ 。在调用这个过程我们假定 $A [i]$ 的左右子树都满足最小堆的性质。但是 $A [i]$ 可能大于 $A [L E F T (i)]$ 或 $A [R I G H T (i)]$ ，这就不满足最小堆的性质。维护堆的过程通过让 $A [i]$ 在最小堆中"逐级下降"，从而使得以 $A [i]$ 为根节点的子树满足堆的性质。

#define PARENT(i) (i-1)/2
#define LEFT(i) 2*i+1
#define RIGHT(i) 2*(i+1)
//维护最小堆
void Min_Heapify(vector<int> &A,int i,int heapSize){
    int left = LEFT(i);
    int right = RIGHT(i);

    int min = i;

    if(left<heapSize&&A[min]>A[left]){
        min = left;
    }
    if(right<heapSize&&A[min]>A[right]){
        min = right;
    }

    if(min != i){
        //交换
        swap(A[i],A[min]);
        Min_Heapify(A,min,heapSize); 
    }
    
}

时间复杂度分析：对于以一棵以 $A [i]$ 为根节点，大小为 $n$ 的子树， $Min\_Heapify$ 的时间代价包括：调整 $A [i]$ 与其子节点的关系时间代价 $\Theta(1)$ ,加上在 $A [i]$ 子树上运行 $Min\_Heapify$ 的时间代价。这个子树的最大为2n/3(最坏情况发生在树的底层恰好半满的时候，如下图)。因此可得递归式：
$T(n)\le T(2n/3)+\Theta(1)$
由主定理可得 $T(n)=O(\lg n)$

最坏情况(示例)：

在这里插入图片描述

建堆

可以通过自底向上的方法利用维护堆的过程把一个数组转换成最小堆。

void BulidMinHeap(vector<int> &A,int heapSize){
    //从非叶节点开始
    for(int i = heapSize/2;i>=0;i--){
        Min_Heapify(A,i,heapSize);
    }
}

时间复杂度分析：对于 $Min\_Heapify$ 其时间复杂度为 $O(\lg n)$ ,会调用 $n$ 次，因此建堆的复杂度为 $O(n\lg n)$ 。的确这个上界是正确的，但不是渐近紧确的。利用以下两个性质可以得到更紧确的界:

含有 $n$ 个元素的堆的高度为 $\lfloor\lg n\rfloor$
高度为 $h$ 的堆最多包含 $\lceil n/2^{h+1}\rceil$ 个节点

因此建堆的代价：
$\sum_{h=0}^{\lfloor\lg n\rfloor}\lceil n/2^{h+1}\rceil O(h)=O(n\sum_{h=0}^{\lfloor\lg n\rfloor}\frac{h}{2^h})$
对于
$\sum_{h=0}^{\lfloor\lg n\rfloor}\frac{h}{2^h}$
的求法。

解释如下：

对于无穷递减几何级数：
$\sum_{i=0}^{\infin }x^k=\frac{1}{1-x},|x|<1\\两边对x求导得：\sum_{i=0}^{\infin }kx^{k-1}=\frac{1}{(1-x)^2},|x|<1\\两边同乘以x得：\sum_{i=0}^{\infin }kx^{k}=\frac{x}{(1-x)^2},|x|<1\\于是有：\sum_{h=0}^{\lfloor\lg n\rfloor}\frac{h}{2^h}=\frac{1/2}{(1-1/2)^2}=2$
所以有：建堆的代价时间复杂度为 $O (n)$

堆排序

堆排序算法，首先将输入数组 $A [1 \dots \dots n]$ 建成最大堆，其中 $n = A . l e n g t h$ 。然后交换 $A [0]$ 与 $A [n]$ 。就能将最小元素放在最尾，然后减少 $h e a p s i z e$ 。重新建堆,再进行交换。以此往复，就能得到排序的数组。

void HeapSort(vector<int> &A){
    BulidMinHeap(A,A.size());\\第2参数为heapSize
    for (size_t i = A.size(); i > 1 ; i--)
    {
        swap(A[0],A[i-1]);
        Min_Heapify(A,0,i-1);\\第3参数为heapSize
        
    }
}

时间复杂度分析：首先建堆为 $O (n)$ ,进行了 $n - 1$ 次的维护,一共是 $O(n\lg n)$ 。因此堆排序的时间复杂度是 $O(n\lg n)$ 。

完整测试代码：

#include <iostream>
#include <vector>
using namespace std;

#define PARENT(i) (i-1)/2
#define LEFT(i) 2*i+1
#define RIGHT(i) 2*(i+1)

//维护最小堆
void Min_Heapify(vector<int> &A,int i,int heapSize){
    int left = LEFT(i);
    int right = RIGHT(i);

    int min = i;

    if(left<heapSize&&A[min]>A[left]){
        min = left;
    }
    if(right<heapSize&&A[min]>A[right]){
        min = right;
    }

    if(min != i){
        //交换
        swap(A[i],A[min]);
        Min_Heapify(A,min,heapSize); 
    }
    
}

void BulidMinHeap(vector<int> &A,int heapSize){
    for(int i = heapSize/2;i>=0;i--){
        Min_Heapify(A,i,heapSize);
    }
}

void HeapSort(vector<int> &A){
    BulidMinHeap(A,A.size());
    for (size_t i = A.size(); i > 1 ; i--)
    {
        swap(A[0],A[i-1]);
        Min_Heapify(A,0,i-1);
        
    }
}
int main(){
    vector<int> v1 = {7,9,8,4,5,9,10};
    HeapSort(v1);
    for(auto x: v1) cout<<x<<",";
    system("pause");
    return 0;
}

优先队列（priority queue)

优先队列（priority queue)是一种用来维护由一组元素构成的集合 $S$ 的数据结构。其中每个元素都有一个有关的值，称为关键字（key)。

以最小优先队列为例。一个最小优先队列应该支持的操作：

$I N S E R T (S, x)$ ：把元素 $x$ 插入到集合 $S$ 中。这一操作等价于 $S=S\cup x$ ，时间复杂度 $O(\lg n)$
$M I N I M U M (S)$ ：返回 $S$ 中具有最小关键字的元素，时间复杂度 $\Theta(1)$
$E X T R A C T - M I N (S)$ ：去掉并返回 $S$ 中的具有最大关键字的元素，时间复杂度 $O(\lg n)$
$D E C R E A S E - K E Y (S, x, k)$ ：将元素 $x$ 的关键字值减少到 $k$ ,这里假设 $k$ 的值不大于 $x$ 的原关键字,，时间复杂度 $O(\lg n)$

如何用堆实现最小优先队列？直接上代码（内附部分注释）：

#include <iostream>
#include <vector>
#include <cstdlib>
using namespace std;

#define PARENT(i) (i-1)/2
#define LEFT(i) 2*i+1
#define RIGHT(i) 2*(i+1)

void Min_Heapify(vector<int> &A,int i,int heapSize){
    int left = LEFT(i);
    int right = RIGHT(i);

    int min = i;

    if(left<heapSize&&A[min]>A[left]){
        min = left;
    }
    if(right<heapSize&&A[min]>A[right]){
        min = right;
    }

    if(min != i){
        //交换
        swap(A[i],A[min]);
        Min_Heapify(A,min,heapSize); 
    }
    
}

void BulidMinHeap(vector<int> &A,int heapSize){
    for(int i = heapSize/2;i>=0;i--){
        Min_Heapify(A,i,heapSize);
    }
}

void HeapSort(vector<int> &A){
    BulidMinHeap(A,A.size());
    for (size_t i = A.size(); i > 1 ; i--)
    {
        swap(A[0],A[i-1]);
        Min_Heapify(A,0,i-1);
        
    }
}

class priority_queue
{
private:
    vector<int> key_heap;
    int heapsize;
public:

    priority_queue(const vector<int> &data):key_heap(data),heapsize(data.size()){
        BulidMinHeap(key_heap,heapsize);
    };
    ~priority_queue(){};

    //返回最小元素
    int Minimun(){
        return key_heap[0];
    }
    //剔除最小元素，并返回它
    int ExtractMin(){
        if(heapsize<1) {
            cout<<"error:heapsize小于1"<<endl;
            return INT32_MIN;
        }
        int min = key_heap[0];
        swap(key_heap[0],key_heap[heapsize-1]);
        --heapsize;
        Min_Heapify(key_heap,0,heapsize);
        return min;
    }
    //将key_heap[i]减少至key
    void DecreaseKey(int key,int i){
        if(i>heapsize) {
            cout<<"超出堆大小"<<endl;
            return;
        }
        if(key_heap[i]<key) {
            cout<<"key太大"<<endl;
            return;
        }
        key_heap[i] = key;
        //维护堆
        while(i>0&&key_heap[i]<key_heap[PARENT(i)]){
            swap(key_heap[i],key_heap[PARENT(i)]);
            i = PARENT(i);
        }
    }
    //insert key
    void InsertKey(int key){
        heapsize++;
        if(heapsize>key_heap.size()){
            key_heap.push_back(INT32_MAX);
        }else
        {
            key_heap[heapsize-1] = INT32_MAX;
        }
        DecreaseKey(key,heapsize-1);
    }

    //重载一个操作符，方便访问元素
    int& operator[](int i){return key_heap[i];}
    //返回对大小
    int HeapSize(){return heapsize;}
};

int main(){
    vector<int> testdata = {19,6,7,23,2,3};
    priority_queue p1(testdata);
    //查看是否建成最小堆
    for(size_t i = 0; i < p1.HeapSize(); i++){cout<<p1[i]<<",";}//输出2,6,3,23,19,7,确实是最小堆
    cout<<endl;
    cout<<"堆大小:"<<p1.HeapSize()<<endl;//输出6

    //测试 ExtractMin,连续剔除7次
    for (size_t i = 0; i < 7; i++)
    {
        cout<<"拿出:"<<p1.ExtractMin()<<","<<"堆大小变为:"<<p1.HeapSize()<<endl;
    }
    cout<<endl;

    //测试insert key
    cout<<"新插入元素:";
    for (size_t i = 0; i < 10; i++)
    {   
        int new_key = i;
        new_key = rand()%100;
        cout<<new_key<<",";
        p1.InsertKey(new_key);

    }
    cout<<endl;
    for(size_t i = 0; i < p1.HeapSize(); i++){cout<<p1[i]<<",";}
    system("pause");
    
}

Reference

《算法导论》第六章
堆维基百科