图论之最短路径 Dijkstra算法、超级源点、反向建边

1.最短路径问题

最短路径问题：求一个结点到另一个结点的权值总和最小的路径

对于无向图和有向图均是成立的

比如下图，求从结点0到结点6的最短路径

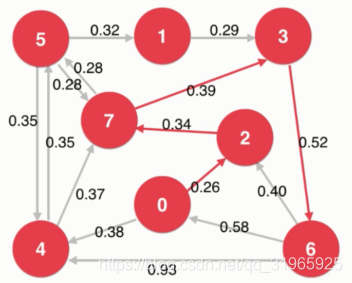
主要应用于：路径规划和工作任务规划

2.松弛操作

松弛操作是最短路径求解的核心

松弛操作：针对从0->1的最短路径，从0到1的权值是5，

此时我们尝试绕着从0->2->1，看下这样的走法所得到的权值是否小于直接从0->1

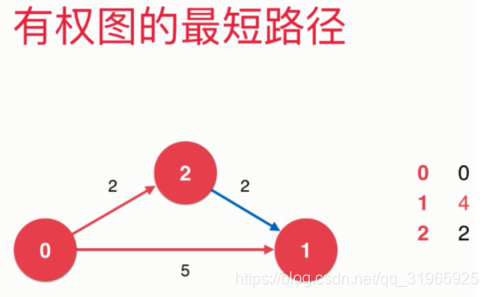
3.Dijkstra单源最短路径算法

这个算法的前提是图中不存在负权边（权值为负数）

算法过程：求0到其他点的最短路径

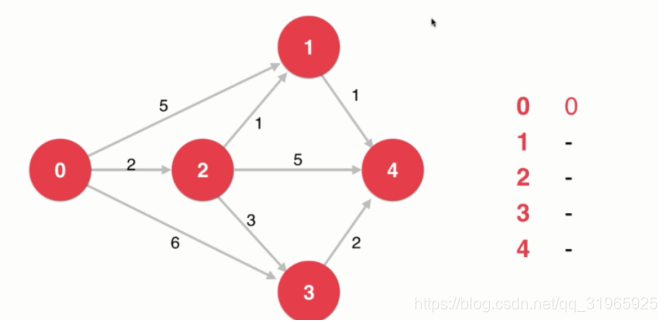
1.对起点做了标识，同时对起点所有的邻边进行了访问，更新数组

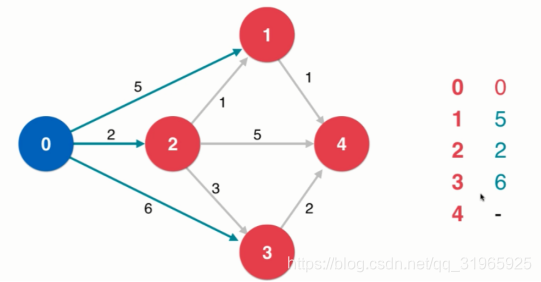
这时候，在所有路径中，0点到2结点的花费最少，那么这条边一定是最终的结果。因为如果从0->别的结点->2，一定花费的更多（注意：这边是保证了图中没有负权边）

2.我们对2进行松弛操作:从2出发，查看2所有的邻边，看下有没有比直接从0结点出发到某结点的路径要小

从2-1的权值为1，加上0-2的权值2，所以花费为3，比5小，更新

从2-4的权值为5，加上0-2的权值2，所以花费为7，还没有值，更新

从2-3的权值为3，加上0-2的权值2，所以花费为5，比6小，更新

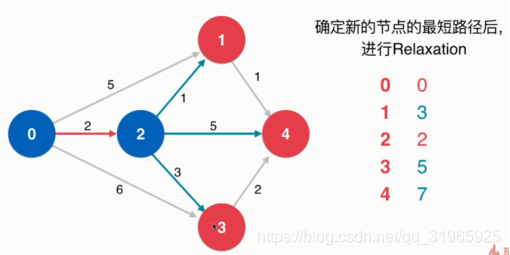
3.现在还没找到最短路径的顶点中，0-1顶点的花费最小，那么就确定当前0-1一定是最终结果

对1进行松弛操作

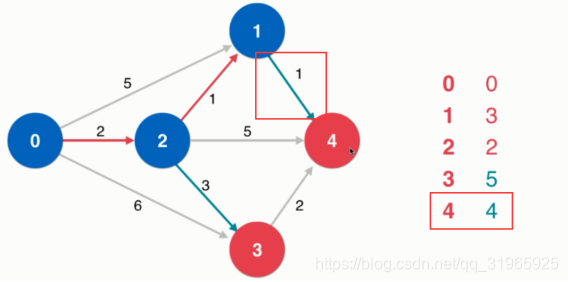
4.现在还没找到最短路径的顶点中，0-4顶点的花费最小，那么就确定当前0-4一定是最终结果

对4进行松弛操作,