数据结构之图--最小生成树（普里姆（Prim）算法）

（在通信网络上用的多）

构造连通网的最小代价生成树称为最小生成树。（找到最小代价连接所有结点）（n个顶点则要找n-1条边出来）

两种构建最小生成树的方法：普里姆（Prim）算法和克鲁斯卡尔（Kruskal）算法

一、普里姆（Prim）算法（时间复杂度n²）（加点法）

    思想：每次迭代寻找与已加入生成树的点所组成最小边长的非生成树中的点，将此点加入树中，由此循环。

        根据思想需要定义两个一维数组：树中顶点下标adjvex[MAXVEX]，（例如：adjvex[2]=8，adjvex[8]=4表示点4连着点8，点8连着点2）；边长矩阵lowcost[MAXVEX]，lowcost[j]=0表示点j加入了生成树，每次迭代在lowcost[i]中选出非0的最小值保存下标i，lowcost[i]存着非生成树中点i连接生成树中点的最小边长；用if(lowcost[j]!=0 && G.arc[k][j] < lowcost[j]) 来改变非生成树中点j连接生成树中点的最小边长和j所连接生成树中点k（即adjvex[j]=k）。

·

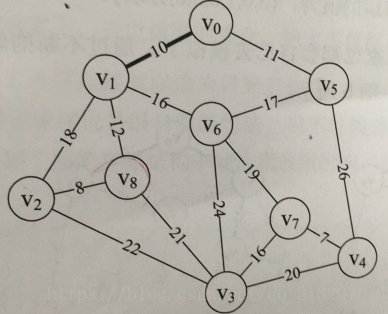
上图在执行代码过程中lowcost变化过程：{0,10,65535,65535,65535,11,65535,