数据结构之图--图的存储结构

一、图的定义

    图（Graph）是由有穷非空顶点和顶点之间边的集合组成，通常表示为：G(V, E)，其中，G表示一张图，V(vertex)是图G中顶点的集合，E（edge）是图G中边的集合。

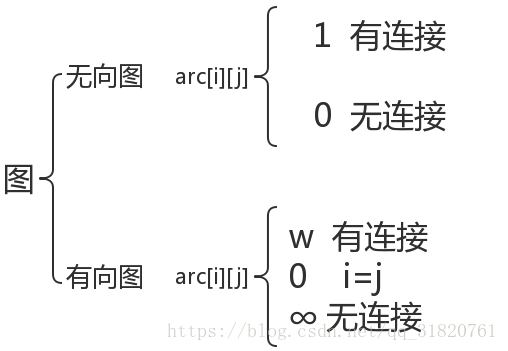
    图分为：有向图（无向边）和无向图（有向边也称为弧Arc,弧表示为 <Vi, Vj>，其中Vi为弧尾，Vj为弧头，弧是由弧尾指向弧头）

    简单图：若不存在顶点到其自身的边，且同一条边不重复出现。

    无向完全图：在无向图中，如果两个顶点之间都存在边。同样道理，有向完全图。

    权（weight）：与图的边或弧相关的数叫做权。

    网（Network）：带权的图。

    稀疏图：有很少条边或弧（边的条数|E|远小于|V|²）的图称为稀疏图（sparse graph），反之边的条数|E|接近|V|²，称为稠密图（dense graph）。

    入度（Indegree）：以顶点Vi为弧头的数目称为入度。同理，出度。

    连通图（Connected Graph）：如果对于图中任意两个顶点Vi、Vj都是连通的（即都有路径），则称G是连通图。

    强连通图：在有向图中，连通图称为强连通图。

    回路或环：路径转一圈能回到起始点。

    生成树：无向图中连通且N个顶点N-1条边。

    有向树：有向图中一顶点入度为0其余顶点入度为1。

    

二、图的存储结构

    存储结构有5种：邻接矩阵、邻接表、十字链表、邻接多重表、边集数组

1、邻接矩阵（用的多）

邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储顶点，一个二维数组（称为邻接矩阵）存储边或弧的信息。

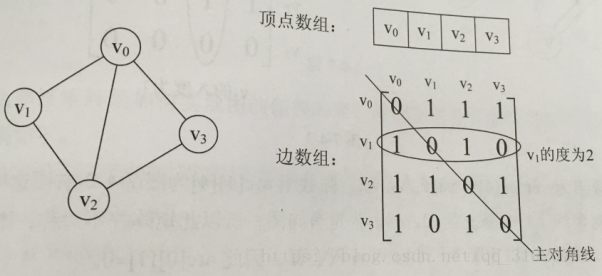
实现代码：（无向图的代码）

#include <stdio.h>

typedef char VertexType;       /*顶点类型*/

typedef int EdgeType;          /*边上权值类型*/

#define MAXVEX 100             /*最大顶点数，根据需求更改*/

#define INFINITY 65535         /*用65535表示无穷大*/

typedef struct MGraph
{
	VertexType vexs[MAXVEX];           /*顶点表*/
	EdgeType arc[MAXVEX][MAXVEX];      /*邻接矩阵，可看做边表*/
	int numVextexes, numEdges;         /*图中当前顶点数和边数*/
}MGraph;

void CreateMGraph(MGraph *G)
{
	int i, j, k, w;
	printf("输入顶点数和边数：\n");
	scanf("%d, %d", &G->numVextexes, &G->numEdges);  /*读入顶点数和边数*/
	for( i = 0; i < G->numVextexes; i++ )     /*读入顶点信息，建立顶点表*/
	{
		printf("请输入类型为char的各个顶点的值");
		scanf("%c", &G->vexs[i]);             /*需要修改*/
	}
	for( i = 0; i < G->numVextexes; i++ )    /*邻接矩阵初始化*/
		for( j = 0; j < G->numVextexes; j++ )
			G->arc[i][j] = INFINITY;
	for( k = 0; k<G->numEdges; k++ )         /*读入numEdges条边，建立邻接矩阵*/     /*因为在此建立的是无向图，所以K<G->numEdges*/
	{
		printf("输入边(Vi,Vj)的上标i，下标j和权w:\n");
		scanf("%d%d%d", &i, &j, &w);     
		G->arc[i][j] = w;
		G->arc[j][i] = G->arc[i][j];         /*因为是无向图，矩阵对称*/
	}
}

2、邻接表（数组与链表相结合）

1、图中顶点用一个一维数组存储：对于顶点数组中，每个数据元素还需要存储指向第一个邻接点的指针，以便查找该顶点的边信息；

2、图中Vi的所有邻接点构成一个线性表（因为邻接点的个数不定，所以用单链表）。

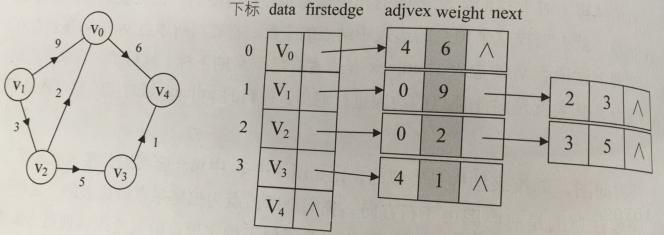
代码实现：（无向图）

#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>

typedef char VertexType;           /*顶点类型*/

typedef int EdgeType;              /*边上的权值*/

#define MAXVEX 100             /*最大顶点数，根据需求更改*/

typedef struct EdgeNode            /*边表结点*/
{
	int adjvex;                    /*邻接点域，存储该顶点对应的下标*/
	EdgeType weight;               /*用于存储权值，对于非网图可以不需要*/
	struct EdgeNode *next;         /*链域，指向下一个邻接点*/
}EdgeNode;

typedef struct VertexesNode        /*顶点表结点*/
{
	VertexType data;               /*顶点域，存储顶点信息*/
	EdgeNode *firstedge;           /*边表头指针*/
}VertexesNode, AdjList[MAXVEX];

typedef struct
{
	AdjList adjlist;
	int numVextexes, numEdges;
}GraphAdjList;

/*建立图的邻接表结构*/
void CreateALGraph(GraphAdjList *G)
{
	int i, j, k;
	EdgeNode *e;
	printf("输入顶点数和边数:\n");
	scanf("%d%d", &G->numVextexes, &G->numEdges);   /*输入顶点数和边数*/
	
	for( i = 0; i < G->numVextexes; i++ )    /*建立顶点表*/
	{
		scanf("%c", &G->adjlist[i].data);    /*输入顶点信息*/
		G->adjlist[i].firstedge = NULL;      /*将边表置为空表*/
	}
	
	/*头插法建立边表*/
	for( k = 0; k < G->numEdges; k++ )       /*建立边表*/
	{
		printf("输入边(Vi,Vj)上的定边序号：\n");
		scanf("%d%d", &i, &j);          
		e = ( EdgeNode * )malloc( sizeof(EdgeNode) );
		e->adjvex = j;                  /*邻接序号为j*/
		e->next = G->adjlist[i].firstedge;   /*将e指针指向当前顶点指向的结点*/
		G->adjlist[i].firstedge = e;        /*将当前顶点的指针指向e*/
	}
}