数据结构之平衡二叉树（AVL）

一、概念

    平衡二叉树是一种二叉排序树，其中每一个节点的左子树和右子树的高度差至多等于1。

    平衡因子（BF）：结点的左子树深度减去右子树深度的值称为平衡因子。

    最小不平衡子树：插入进来一个元素后，变得不平衡的最小部分。

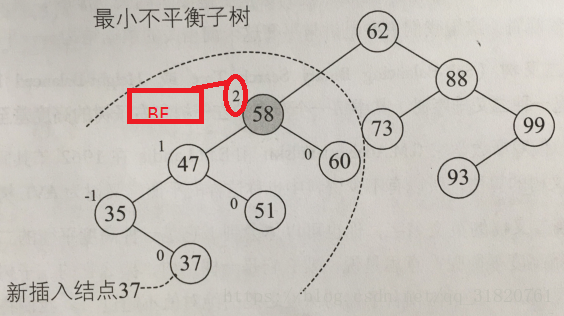
二、实现原理

    当最小不平衡子树根结点的平衡因子BF大于1时，则右旋，小于-1时，则左旋；

插入结点后，最小不平衡子树的BF与它的子树的BF符号相反时，先将结点进行一次旋转使得符号相同后，再反方向旋转一次。

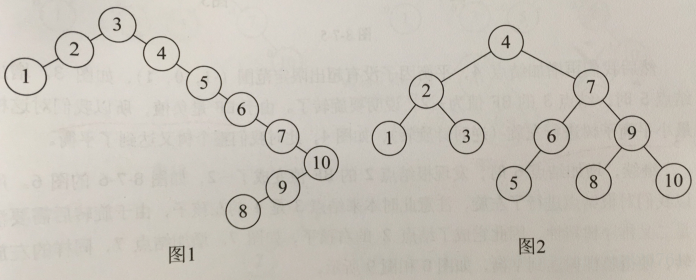
将图1中的二叉排序树变为图二中的平衡二叉树：

1、左旋情况

 

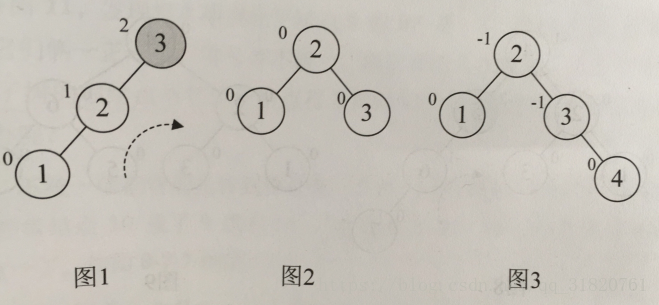
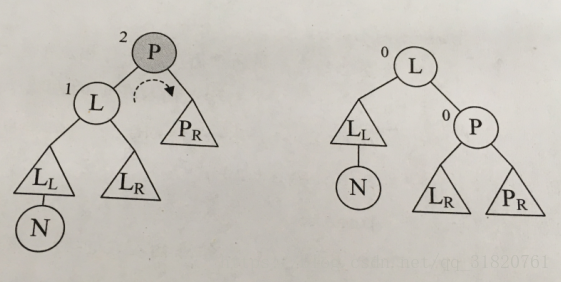
2、右旋情况

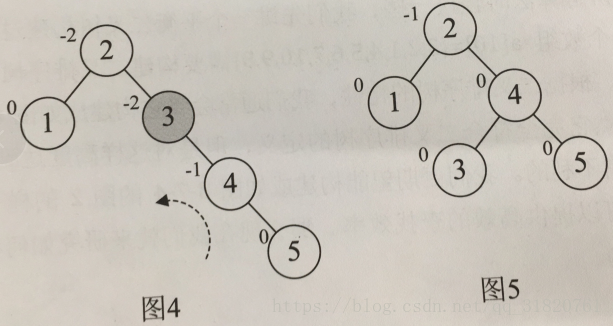
3、需要先旋转一次将符号变成一致，在反方向旋转一次得到平衡（分开写的话这里包含两种情况）

   

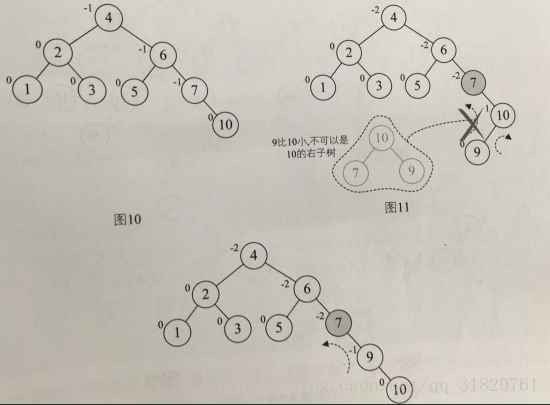
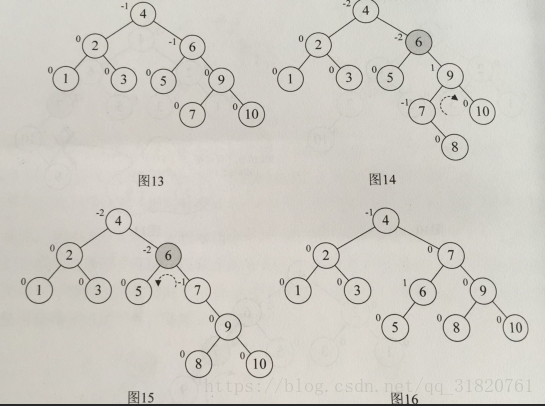
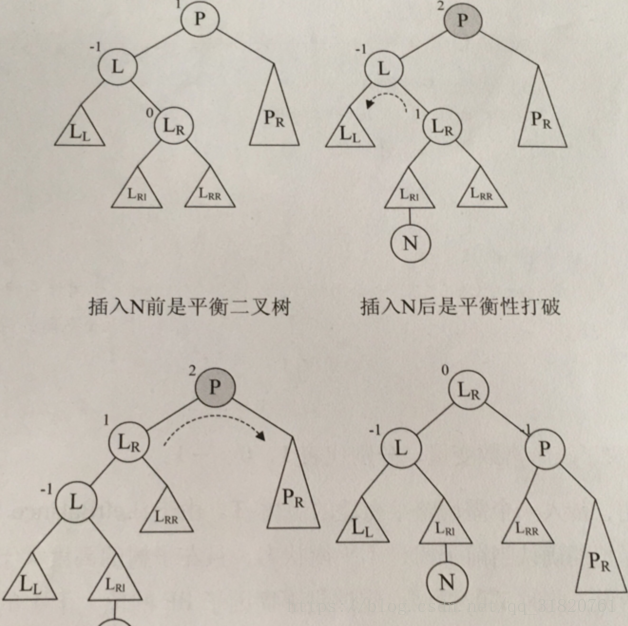
三、代码实现

    当一个元素插入进左子树后，有三种情况：1、插入进来后树的左比右高2，则需要做左平衡；2、插入进来后左比右高1或者等高，不做平衡变换；

    同理：当一个元素插入进右子树后，也有三种情况。

注意：做左平衡时有两种情况，一种是只做一次单右旋；一种是做一次单左旋，再做一次单右旋。

//1、右旋函数
void r_Rotate(tNode *t)   //*t指向根结点
{
	tNode temp;
	temp = *t;
	*t = (*t)->lchild;
	temp->lchild = (*t)->rchild;
	(*t)->rchild = temp;
}

//2、左旋函数
void l_Rotate(tNode *t)   //*t指向根结点
{
	tNode temp;
	temp = *t;
	*t = (*t)->rchild;
	temp->rchild = (*t)->lchild;
	(*t)->lchild = temp;
}

//3、最小不平衡子树的BF与它的子树的BF符号相反时，先将结点进行一次旋转使得符号相同后，再反方向旋转一次
//3.1根结点bf为正2，左子树的bf为-1:先将左子树左旋，再整个树右旋
void l_r_Rotate(tNode *t)
{
	//左子树左旋
	l_Rotate( &((*t)->lchild) );	
	//整个树右旋
	r_Rotate(t);
}
void r_l_Rotate(tNode *t)
{
	//左子树左旋
	r_Rotate( &((*t)->rchild) );	
	//整个树右旋
	l_Rotate(t);
}

注意：不能上述三个函数里面处理bf，因为双旋函数调用了单旋函数，而双旋函数中bf不能那样处理

总代码：

typedef struct treeNode node;

typedef struct treeNode
{
	int data;
	
	int bf;  //平衡因子
	
	node *rchild, *lchild;
	
}node, *tNode;


#define LH +1  //左高
#define EH 0   //等高
#define RH -1  //右高
#define TRUE 1
#define FALSE 0


//创建平衡二叉树
void createAVL(tNode *T)
{
	int e;
	scanf("%d", &e);
	if(65535 != e)
	{
		insertAVL(T, e);
		scanf("%d", &e);
	}	
}

//向平衡二叉树中插入元素
int insertAVL(tNode *T, int e)   
{
	if(!(*T))
	{/*插入新节点，树长高*/
		*T =  (tNode)malloc(sizeof(node));
		(*T)->data = e;
		(*T)->lchild = (*T)->rchild = NULL;
		(*T)->bf = EH;  //默认为等高		
	}
	
	else
	{
		if(e == (*T)->data)
		{//树中已存在和e相同的关键字则结点不再插入
			return FALSE;
		}
		
		if(e < (*T)->data)
		{//则沿着左子树向下找插入点
			if(!insertAVL( &((*T)->lchild), e ))  //未插入
				return FALSE;
			else   //已经插入，并且左子树长高了
			{
				switch((*T)->bf)  //检查T的平衡度 ， 其实真正的bf = (*T)-bf+1
				{
					case LH:   //原本左子树比右子树高，现在插入一个元素后，左子树bf比右子树大2，所以要做做平衡处理
						leftBalance(T);
						break;  
					case EH:   //原本左右等高，现在插入一个元素后，左比右高1
						(*T)->bf = LH;
						break;
					case RH:    //原本右子树比左子树高，现在等高
						(*T)->bf = EH;
						break;						
				}
			}
		}
		
		else
		{//则沿着右子树向下找插入点
			if(!insertAVL( &((*T)->rchild), e ))  //未插入
				return FALSE;
			else   //已经插入，并且左子树长高了
			{
				switch((*T)->bf)  //检查T的平衡度 ， 其实真正的bf = (*T)-bf+1
				{
					case LH:    //原本左子树比右子树高，现在等高
						(*T)->bf = EH;
						break;					
					case EH:   //原本左右等高，现在插入一个元素后，右比左高1
						(*T)->bf = RH;
						break;
					case RH:   //原本右子树比左子树高，现在插入一个元素后，右子树bf比左子树大2，所以要做做平衡处理
						rightBalance(T);
						break; 						
				}
			}
		}
	}
	
	return TRUE;
}


void leftBalance(tNode *T)
{
	tNode L, Lr;
	L = (*T)->lchild;
	
	switch(L->bf)   //不可能是等高EH
	{//检查左子树的平衡度，由此做出相应的平衡处理
		case LH:   //表明新节点是插入在T的左孩子的左子树上面，所以做右旋
			(*T)->bf = ((*T)->lchild)->bf = EH;   //旋转后的平衡因子bf
			r_Rotate(T);
			break;
		case RH:   //表明新节点是插入在T的左孩子的右子树上面，所以做双旋
			/*处理旋转后平衡因子bf的值*/
			Lr = L->rchild;
			switch(Lr->bf)  //修改对应的t及其左孩子的平衡因子bf
			{
				case LH:
					(*T)->bf = RH;
					L->bf = EH;
					break;
				case EH:
					(*T)->bf = L->bf = EH;
				case RH:
					(*T)->bf = EH;
					L->bf = LH;
					break;
			}
			Lr->bf = EH;
			/*bf处理结束*/	
			l_r_Rotate(T);
			break;
	}
}

void rightBalance(tNode *T)
{
	tNode R, Rl;
	R = (*T)->rchild;
	
	switch(R->bf)   //不可能是等高EH
	{//检查左子树的平衡度，由此做出相应的平衡处理
		case RH:   //表明新节点是插入在T的右孩子的右子树上面，所以做左旋
			(*T)->bf = ((*T)->rchild)->bf = EH;   //旋转后的平衡因子bf
			l_Rotate(T);
			break;
		case LH:   //表明新节点是插入在T的右孩子的左子树上面，所以做双旋
			/*处理旋转后平衡因子bf的值*/
			Rl = R->lchild;
			switch(Rl->bf)  //修改对应的t及其右孩子的平衡因子bf
			{
				case RH:
					(*T)->bf = LH;
					R->bf = EH;
					break;
				case EH:
					(*T)->bf = R->bf = EH;
				case LH:
					(*T)->bf = EH;
					R->bf = RH;
					break;
			}
			Rl->bf = EH;
			/*bf处理结束*/	
			l_r_Rotate(T);
			break;
	}
}


//1、右旋函数, 注意：不能再这里面处理bf，因为双旋函数调用了它，而双旋函数中bf不能这样处理
void r_Rotate(tNode *t)   //*t指向根结点
{
	tNode temp;
	temp = *t;
	*t = (*t)->lchild;
	temp->lchild = (*t)->rchild;
	(*t)->rchild = temp;
}

//2、左旋函数
void l_Rotate(tNode *t)   //*t指向根结点
{
	tNode temp;
	temp = *t;
	*t = (*t)->rchild;
	temp->rchild = (*t)->lchild;
	(*t)->lchild = temp;
}

//3、最小不平衡子树的BF与它的子树的BF符号相反时，先将结点进行一次旋转使得符号相同后，再反方向旋转一次
//3.1根结点bf为正2，左子树的bf为-1:先将左子树左旋，再整个树右旋
void l_r_Rotate(tNode *t)
{	
	//左子树左旋
	l_Rotate( &((*t)->lchild) );	
	//整个树右旋
	r_Rotate(t);
}
void r_l_Rotate(tNode *t)
{	
	//左子树左旋
	r_Rotate( &((*t)->rchild) );	
	//整个树右旋
	l_Rotate(t);
}


void PreOrderTraverse(tNode T)   /*前序遍历算法*/
{
	if( NULL == T )
		return;
	printf("%d-->", T->data);	      //先显示根结点
	PreOrderTraverse(T->lchild);   //再遍历左子树
	PreOrderTraverse(T->rchild);   //最后遍历右子树
}