ML-01-线性回归以及代码实现

最新推荐文章于 2025-03-06 21:23:35 发布

Scathon

最新推荐文章于 2025-03-06 21:23:35 发布

阅读量567

点赞数

分类专栏：机器学习

本文链接：https://blog.youkuaiyun.com/qq_31617409/article/details/83244168

版权

机器学习专栏收录该内容

3 篇文章

订阅专栏

一、表示方式以及数学符号解释

准备工作：

训练数据集
attr1	attr2	value
1.3	1.9	3.2
1.1	1.5	2.5
1.5	2.3	3.9
1.7	2.7	4.6
1.9	3.1	5.3
2.1	3.5	6
3.2	5.1	10
2.3	3.9	6.7
2.5	4.3	7.4
还有一些数据...主要是为了下文实现梯度下降算法的实验数据

特征 feature： $x_{i}$ ，代表一个训练样本的第i个特征属性，以上面训练数据集为例， $x_{j}^{i}$ 表示，第 i 个样本的第 j 个属性
特征向量：x, 特征向量有特征属性值组成,一般情况下，x是n维向量，其中n指的是特征向量的特征值的数量。以上面的数据集为例，n=2，注意最后一列是输出值，并不是特征值（以吴恩达机器学习教程中的房价预测为例，前两列可以分别指的是，房屋面积，街道宽度，那么最后一列就是房价）
输出向量：y， $y^{(i)}$ 表示第i个样本输出的值
预测函数：

$h_{\Theta }\left ( x \right )=\Theta_{0}+\Theta_{1}x_{1}+\Theta_{2}x_{2}+\cdot \cdot \cdot +\Theta_{n}x_{n}=\Theta^{T}x$

注意，输入矩阵X是一个n+1矩阵，因为我们加了一列 $x_{0}^{i}=1$ for (i ∈ 1 to m)

θ是回归系数，也是一个n+1维向量

二、误差函数

既然是预测，那么就需要一个手段评定我们的学习效果。这里就是评估，与测试与实际值之间的差距。也就是 $\Theta^{T}x^{i}$ 与 $y^{(i)}$ 之间的差异，常见的一种方法就是最小均方来描述误差：

$J\left ( \Theta \right )=\frac{1}{2m}\sum_{i=1}^{m}\left ( h_{\Theta}(x^{(i)})-y^{(i)} \right )^2$ 其中 m 是样本数量

其实上面的表达式可以用一个简单的矩阵表达式进行表示（学线性代数的时候不知道这玩意具体是干啥的，现在才知道，线性代数真的是牛逼的东西）： $J({\Theta})=\frac{1}{2m}(X\Theta-y)^{T}(X\Theta-y)$

误差评估的函数在机器学习里面也叫代价函数

三、梯度下降

3.1-批量梯度下降算法

首先，梯度下降公式如下：

$\Theta_{j}=\Theta_{j}-\alpha\frac{\delta }{\delta\Theta_{j}}J(\Theta)$ 其中 α 是学习率。

数学中，函数的梯度方向是变化最快的方向，基于这一点，沿着 $\bigtriangledown J(\Theta)$ 的方向走，那么就能很快到达最小值或者是极小值。对于学习率 $\alpha$ ，如果设置比较大，你懂得，容易跨越过最小值。 $\alpha$ 太小的话，就会造成收敛速度很慢，实际中，可以将 $\alpha$ 以3倍，10倍这种比率进行取值尝试。

对于一个样本容量是m的训练数据集来说，θ的调优过程如下：

-----------------------------------------------------------------------------------

for i 1 to n:

$\Theta_{j}=\Theta_{j}-\alpha\frac{1}{m}\sum_{i=1}^{m}(h_{\Theta}(x^{(i)})-y^{(i)}))x^{(i)}_{j}$

公式3-1（记住这个编号）

-------------------------------------------------------------------------------------

表达成矩阵就是：

其中代价函数是：

$J\left ( \Theta \right )=\frac{1}{2m}\sum_{i=1}^{m}\left ( h_{\Theta}(x^{(i)})-y^{(i)} \right )^2$ 我们对 $J(\Theta)$ 针对 $\Theta_{j}$ 进行求导就得出了公式3-1 右边的部分，也就是梯度部分。

求导过程：

这种过程是基于最小均方（LMS）的批量梯度下降算法，一方面，这个方法可以收敛到最小值，缺点是每调节一个 $\Theta_{j}$ 就要便利整个数据集，如果样本数据集很大，那么开销非常大。但是，该过程可以用更简单的矩阵计算方式，可以利用并行计算来优化性能。

3.1.1 更简洁的公式表示方式。

公式3-1，要利用迭代操作计算一轮迭代过程的所有θ值，其实，我们可以用更简洁的矩阵表示方式来计算，这样在实际编程中，利用python的一些科学计算包，例如numpy将会很简单的实现一个梯度下降解决线性回归的问题。

代价函数： $J(\Theta)=\frac{1}{2m}(X\Theta-y)^{T}(X\Theta-y)$

梯度表示： $\frac{\delta}{\delta(\Theta)} J(\Theta)=\frac{1}{m}X^{T}(X\Theta-y)$

调优过程核心就变成了如下这个简单的矩阵计算公式：

$\Theta=\Theta-\alpha\frac{1}{m}X^{T}(X\Theta-y)$

3.2-随机梯度下降算法

在每次更新时用1个样本，可以看到多了随机两个字，随机也就是说我们用样本中的一个例子来近似我所有的样本，来调整θ，因而随机梯度下降是会带来一定的问题，因为计算得到的并不是准确的一个梯度，对于最优化问题，凸问题，虽然不是每次迭代得到的损失函数都向着全局最优方向，但是大的整体的方向是向全局最优解的，最终的结果往往是在全局最优解附近。但是相比于批量梯度，这样的方法更快，更快收敛，虽然不是全局最优，但很多时候是我们可以接受的，所以这个方法用的也比上面的多

-----来自知乎大佬的回答

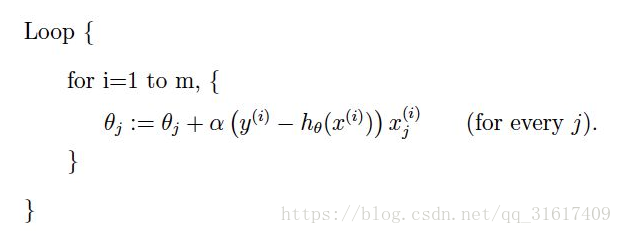
二者比较：

手段	概括	优点	缺点
批量梯度下降方法	尽可能减小训练样本的总的预测代价	能够获得最优解，支持并行计算	样本容量较大的时候，性能显著下降
随机梯度下降方法	尽可能的减小每个训练样本的预测代价	训练速度快	并不一定获得全局最优解，经常出现抖动和噪音，且不能通过并行计算进行优化。

四、实现代码

# 线性规划梯度下降算法Version1
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
from numpy import random


# 计算梯度向量
def generate_gradient(X, theta, y):
    sample_count = X.shape[0]
    # 计算梯度，采用矩阵进行计算，代码很简洁
    return (1./sample_count)*X.T.dot(X.dot(theta)-y)


# 读取训练集数据
def get_training_sample_data(file_path):
    ori_data = np.loadtxt(file_path, delimiter=",")
    cols = ori_data.shape[1]
    return (ori_data, ori_data[:, :cols - 1], ori_data[:, cols-1:])

# 初始化θ数组
def init_theta(feature_count):
    return np.ones(feature_count).reshape(feature_count, 1)


# 记录J(θ)的变化趋势，验证梯度下降是否运行正确
diff_value = []


def gradient_descend_kernal(X, theta, y, step):
    h = (X.dot(theta)-y).T.dot(X.dot(theta)-y)
    index = 0
    init_gradient = generate_gradient(X, theta, y)
    while not np.all(np.absolute(init_gradient) <= 1e-5):
        theta = theta - step * init_gradient
        init_gradient = generate_gradient(X, theta, y)
        # 计算误差值
        h = (X.dot(theta)-y).T.dot(X.dot(theta)-y)
        if (index+1) % 10 == 0:
            diff_value.append((index, h[0]))
        index += 1
    return theta


def visualJTheta(diff_value):
    p_x = []
    p_y = []
    for (index, sum) in diff_value:
        p_x.append(index)
        p_y.append(sum)
    plt.plot(p_x, p_y, 'b', label="difference function")
    plt.show()
    x = np.linspace(0, p_x[len(p_x) - 1], len(p_x))

# 可视化
def visualization(theta, sample_training_set):
    fig = plt.figure()
    ax = Axes3D(fig)
    plt.title("Linear Regression With Gradient Descend")
    ax.legend()
    ax.set_xlabel('X', color='r')
    ax.set_ylabel('Y', color='g')
    ax.set_zlabel('Z', color='b')
    x, y, z = sample_training_set[:,
                                  1], sample_training_set[:, 2], sample_training_set[:, 3]
    ax.scatter(x, y, z, c='b')  # 绘制数据点
    X, Y = np.meshgrid(sample_training_set[:, 1], sample_training_set[:, 2])
    Z = theta[0] + theta[1]*X + theta[2]*Y
    ax = fig.gca(projection='3d')
    surf = ax.plot_surface(X, Y, Z, color='g')
    plt.show()


def app_main():
    training_sample_include_y, training_sample, y = get_training_sample_data(
        'F:\MachineLearn\ML_Algorithm_Impl\LinearRegression\data\sample.txt')
    sample_count, feature_count = training_sample.shape
    step = 0.01
    theta = init_theta(feature_count)
    result_theta = gradient_descend_kernal(training_sample, theta, y, step)
    print(result_theta)
    visualJTheta(diff_value)
    visualization(result_theta, training_sample_include_y)


if __name__ == '__main__':
    app_main()

数据集可以用文章一开始给的数据集，因为做了可视化，所以特征属性的个数一定是2个。

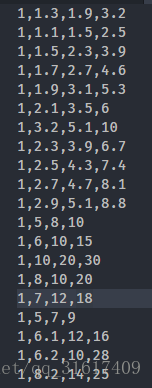
别忘了第一列全部是1,

可视化结果：

代价变化趋势图：

预测函数效果图：

五、正规方程法

上面我们实现线性回归问题的解决是通过梯度下降的方法来解决的，除了利用梯度下降求解代价函数 $J(\Theta)$ ，还可以通过正规方程法来求解（Normal Equation）。

$\Theta=(X^{T}X)^{-1}X^{T}y$

其中，X是输入向量矩阵，第0个特征表示偏置位（ $x_{0}=1$ ）,y 是目标向量，具体推导过程，本屌尚在研究。。。

二者对比--摘自斯坦福大学ML笔记

梯度下降	正规方程
需要选择适当的学习率 α	不要学习率 α
需要进行多步迭代	不需要进行迭代，在 Matlab 等平台上，矩阵运算仅需一行代码就可完成
对多特征适应性较好，能在特征数量很多时仍然工作良好	算法复杂度为 O(n3)O(n3)，所以如果特征维度太高（特别是超过 10000 维），那么不宜再考虑该方法。
能应用到一些更加复杂的算法中，如逻辑回归（Logic Regression）等	矩阵需要可逆，并且，对于一些更复杂的算法，该方法无法工作

内容如有不正确，恳请大家不吝赐教。