浅析机器学习数学基础（2）--方向导数与梯度

最新推荐文章于 2024-07-29 19:00:33 发布
原创 最新推荐文章于 2024-07-29 19:00:33 发布 · 434 阅读 · 1 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#机器学习 #数学 #人工智能

本文深入探讨了方向导数的概念，从偏导数出发，解释了方向导数的几何意义及其与自变量变化的关系。同时，文章详细介绍了梯度的概念，包括其作为向量的性质，以及它与方向导数最大值之间的联系。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

方向导数与梯度

方向导数

关于方向导数的问题，首先要引入偏导数。

偏导数：

函数f(x,y),在(x,y)邻域内有定义，定y = y0,x在f(x,y0)处可导，则x在f(x,y0)处的极限为A

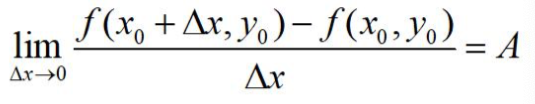
在这里插入图片描述

则A为x在f(x,y0)处的偏导数

几何意义：是方程所描述的曲面（线）在x0处的切线对x轴的斜率

方向导数：

方向导数是随着自变量的一个微小的变化，f(x,y)产生的变化量

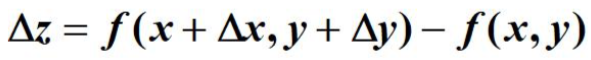
在这里插入图片描述

与∆x和∆y组成的向量l的模

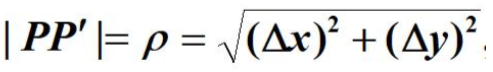
在这里插入图片描述
之间的比值，称为函数在l方向上的方向导数

定理:如果函数在点p(x,y)是可微分的，那么在该点沿任意方向L的方向导数都存在

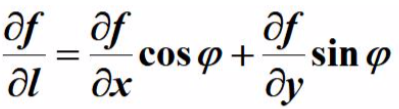
在这里插入图片描述

φ为x轴与l的角度

梯度

梯度是一个向量，它的方向与方向导数最大值取得的方向一致。其大小正好是最大的方向导数

在这里插入图片描述

机器学习过程中看过的一些好文章
scxyz的博客
08-14 1455
说明 1. 作为自己学习的记录会一直进行下去，也方便自己日后再来查看。 2. 如果链接失效，大家可以根据文章名称进行搜索。 3. 每个链接只是博客的一篇文章，进入博客作者的首页一般会有他写的更多优秀文章。 基础知识 数学之美番外篇：平凡而又神奇的贝叶斯方法：http://mindhacks.cn/2008/09/21/the-magical-bayesian-method/
方向导数(Directional derivatives)
空字符
09-08 5万+
方向导数(Directional Derivatives)提到方向导数，我们先来回顾一下导数(Derivative)和偏导数(Partial Derivative)的几何意义。 导数是二维平面中，曲线上某一点沿着x轴方向变化的速率，即函数f(x)f(x)在该点的斜率； 偏导数是在三维空间中，曲面上某一点沿着x轴方向或y轴方向变化的速率，即∂f∂x是函数f(x,y)\frac{\partial f}{
北大数学基础（总结计算机科学论坛上的各家资料得来）
03-28
北大90-09年的图片版数学基础、相关的word文档以及各位网友整理的答案，算是各类类似资源里比较全面的了，拿来与诸位共享！
方向导数和梯度（grad）
qq_42578970的博客
05-30 3万+
方向导数：若u=f(x,y)在点(x0,y0)处可微分，则沿方向el=(cosα,cosβ)的导数为。 其中cos^2(α)+cos^2(β)=1。 对于自变量更多的函数，式子类似，都是函数对于该未知量求偏导后，乘以求导方向的单位向量中的对应项 梯度：若函数在D内具有一阶连续偏导数，则对于D内任意一点(x0,y0)，都可确定一个向量 这个向量就叫函数在点(x0,y0)处的梯度，记作grad f(x,y) 某一点方向导数最大值，就是那一点梯度的膜，最小值则为相反数 在求曲面切平面时
方向导数与梯度
热门推荐
MyArrow的专栏
05-06 11万+
1. 基本概念     方向导数：是一个数；反映的是f(x,y)在P0点沿方向v的变化率。     偏导数：是多个数（每元有一个）；是指多元函数沿坐标轴方向的方向导数，因此二元函数就有两个偏导数。     偏导函数：是一个函数；是一个关于点的偏导数的函数。     梯度：是一个向量。      2. 方向导数     反映的是f(x,y)在P0点沿方向v的变化率。     例子如下
方向导数
pppzzg的博客
12-10 493
详解方向导数
最新发布
二分掌柜的
07-29 2382
flyfish
浅析机器学习数学基础（3）---微积分
YYDGS的博客
12-09 643
微积分 由于此类的工具类知识比较离散，本文包含如下内容： 微积分 微积分思想 几个指标解释 定积分 定积分定义 定积分性质 定积分求解 微积分 微积分的思想 微积分被发明，主要用来解决速度，面积等实际问题，而实际问题一般都是一些非线性的问题，这样计算起来就比较麻烦。 所以微积分引入了以直代曲的思想 计算过程如下： 在a,b之间插入若干个点，这样就有了n个小区间 每个小矩形的面积...
浅析机器学习数学基础（4）----泰勒公式
YYDGS的博客
12-13 1544
泰勒公式 为什么要用泰勒公式呢？ 用简单的熟悉的多项式来近似代替复杂的函数 泰勒公式容易计算函数值，导数与积分仍是多项式 多项式由他的系数完全确定，其系数又由他在一点的函数值及其导数所确定。 代替复杂函数 以直代曲 当|x|很小的时候， 这就相当于，在求一阶导数，求f(x)在某一点的切线，这个从函数整体来看，只能表示出在下一个点上，函数的整体走势是上升还是下降。 如果这时加上二阶导数。如...
人工智能-机器学习-浅析上海DM杂志的广告劝服功能与信息传播功能.pdf
05-20
本文将对《人工智能-机器学习-浅析上海DM杂志的广告劝服功能与信息传播功能》这一论文进行深入解析，探讨人工智能和机器学习背景下，上海DM杂志在广告劝服及信息传播功能方面的应用及其影响。 DM杂志，作为一种直接...
浅析机器学习的发展与应用.pdf
09-24
计算统计学为机器学习提供了概率论与统计推断的基础，数学优化使得机器学习模型可以更加高效地处理数据。数据挖掘利用机器学习技术，在海量的数据中寻找模式和关联，而模式识别则是人工智能领域的一个重要基石，它与...
浅析机器学习在气候研究中的应用.pdf
09-24
"浅析机器学习在气候研究中的应用" 机器学习在气候研究中的应用可以追溯到20世纪90年代，但直到最近几年，机器学习技术的高速发展才使其在气候研究中扮演着越来越重要的角色。机器学习技术可以快速处理大量数据，并...
方向导数和梯度
thehunters的专栏
06-08 9755
考虑函数沿坐标轴方向的变化率是不够的.例如，热空气要向冷的地方流动,气象学中就要确定大气温度、气压沿着某些方向的变化率.因此我们有必要来讨论函数沿任一指定方向的变化率问题.设 是xoy平面上以P0(x0,y0)为始点的一条射线,el=(cosα,cosβ)是与 同方向的单位向量.射线的参数方程为设函数z=f(x,y)在点P0(x0,y0)的某个邻域U(P0)内有定义,P(x0+ tcosα,y0 + tcosβ)为上另一点,且P∈U(P0)如果函数增量f(x0+tcosα,Y0 +tcosβ)-f(x0,y
直观理解机器学习中的梯度与方向导数
qq_37692302的博客
04-05 1611
梯度是方向导数变化最大的方向！！！ 1.方向导数 方向导数的本质是一个数值，简单来说其定义为： 一个函数沿指定方向的变化率。 因此，构建方向导数需要有两个元素： 1) 函数 2) 指定方向 当然，与普通函数的导数类似，方向导数也不是百分之百存在的，需要函数满足在某点处可微，才能计算出该函数在该点的方向导数。 至于其物理含义，这里采用最常用的下山图来表示。 ...
导数、偏导数、方向导数
naozibuok的博客
10-16 1297
导数是描述函数变化率的数学概念。导数的定义式:那么就有一个问题，为什么求函数的最大值点是要对其自变量求导，并使其导数等于0比如:求L(θ)=3lnθ+2ln(1-θ)的最大值点既然导数表示函数的变化率，那么当函数L(θ)的导数等于0，也就是函数L(θ)的变化率等于0，函数不再变化了，这个值唯一了，那么唯一的值只可能是最大值或最小值。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值