AAAI2020 | point2Node 论文解析

最新推荐文章于 2025-10-20 14:21:26 发布

原创

最新推荐文章于 2025-10-20 14:21:26 发布 · 1k 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#深度学习 #python #机器学习 #人工智能 #神经网络

提出一种高维节点图模型，融合点云上的self, local, non-local相关性，设计Gate Mechanism自适应聚合特征。

AAAI2020(oral)《Point2Node: Correlation Learning of Dynamic-Node for Point Cloud Feature Modeling》

paper下载：
https://arxiv.org/abs/1912.10775

github地址：（暂未开源）

这篇文章提出一种高维节点图模型的关系学习网络，在三维点云上融合节点之间的self , local,
non-local correlation（从2d Non-Local Neural Network 中借鉴）三种相关性的相关信息，并设计Gate Mechanism在channel level自适应地聚合feature。在点云分类和分割问题上达到SOTA

这里主要对method部分做具体公式步骤笔记，加深理解。

Method

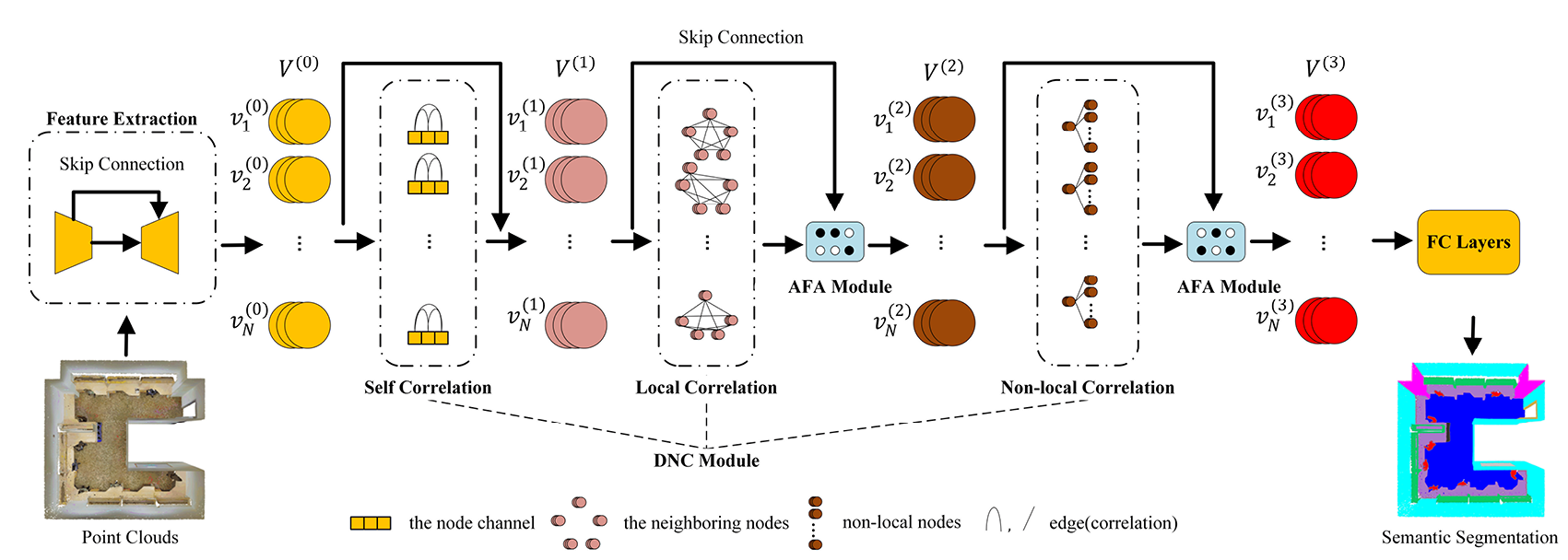
Feature Extraction

目的：将输入变为高维节点 $V^{(0)}$ ，在后续继续转换。

做法：输入：一组无序点
$P=\left\{p_{i} \in R^{3+d}, i=1,2, \ldots, N\}\right.$ N为点的数量，3+d为 $x y z$ 维及附加属性（d=3: rgb或者法向信息）

通过Feature Extraction, 构建高维节点 $V^{(0)}=\left\{v_i^{(0)} \in R^{C}, i=1,2, \ldots, N\}\right.$
每个节点 $v_{i}^{(0)}$ 是点 $p_i$ 的学得的multi-channel特征向量， $C$ 是每个节点的维数。Feature Extraction模块采用PointCNN的X-conv，并构建U-Net用于特征学习

在后面，通过动态节点相关性(DNC) 模块从不同level挖掘点相关性，并动态生成高维节点 $V^{(1)}, V^{(2)}$ 和 $V^{(3)}$ 。然后，自适应特征聚合（AFA）模块自适应聚合不同level学习的节点的feature。最后，高维节点送到fc layer分配label。

动态节点关联模块（DNC）

目的：挖掘不同level的点之间的相关性，把 $V^{(0)}$ 分别生成 $V^{(1)}, V^{(2)}$ 和 $V^{(3)}$
做法：给定初始高维节点
$V^{(0)}=\left\{v_i^{(0)} \in R^{C}, i=1,2, \ldots, N\}\right.$
引入跨通道边（cross-channel edges）和跨节点边（cross-node edges）。
跨通道边：
在同一节点两个通道之间的边，挖掘不同通道之间的相关性。

跨节点边：在不同节点之间的边，有两种类型：

局部边（local edges）：在相邻（空间上靠近）的节点之间，挖掘局部上下文信息
非局部边（non-local ）：
在非局部（空间上较远）节点之间，挖掘潜在的长距离依赖关系。

因此，DNC模块中有三种要学的相关性：Self Correlation, Local Correlation, and Non-local Correlation，下面依次介绍。且在每次相关学习后动态更新高维节点

Self Correlation

目的：用来表示节点的通道之间的依赖性。
做法：用一维可分离卷积实现的MLP来整合单个像素不同通道之间的相关性权重，编码为单个权重（借鉴2D通道权重：卷积汇总图像中一个像素所有的通道），因此，对于每个C维节点 $v_{i}^{(0)} \in V^{(0)}$ ，计算一个C维的通道权重 $w_{i} \in R^{C}$ ：

$w_{i}=M L P\left(v_{i}^{(0)}\right)$
用softmax归一化，让权重在不同通道间具有可比性：
$\overline{w_{i, c}}=\frac{\exp \left(w_{i, c}\right)}{\sum_{j=1}^{C} \exp \left(w_{i, j}\right)}$
$w_{i, c}$ 是wi的第c个元素，