动态规划解决0-1背包问题

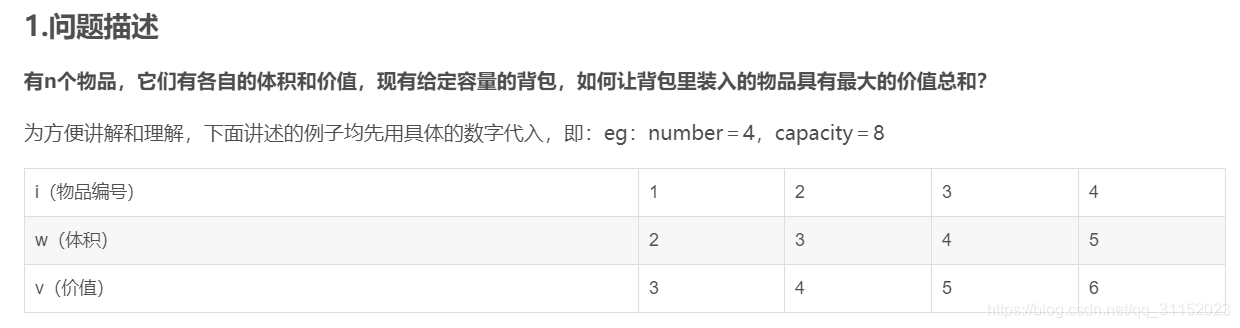
1、使用动态规划算法去解决0-1背包问题，解题思路如下，这个参照网友的，我觉得解释的很清晰。

代码的实现，也是我参照网友的，然后自己理解了一番，然后实现的：

package com.dongTaiGuiHua;

/**
 * 通过构建二维数组找出了当前背包容量能找到的最大值，然后得确定到底选择了哪些商品
 */
public class beibao01V2 {

    public static void main(String[] args) {
        // 商品的数量
        int goodsNums = 8;
        // 背包的容量
        int packageCapcity = 10;
        // 商品对应的重量
        int[] goodsWeight = new int[]{1,2,3,2,2,1,1,2};
        // 商品对应的价值
        int[] goodsValue = new int[]{5,3,1,1,2,2,3,4,1};
        // 声明一个动态规划的数组 行和列多设置了一位是因为要处理0个商品和0容量的背包的情况。这样i就表示的真正的第i个商品
        int[][] tempArr = new int[goodsNums+1][packageCapcity+1];
        // 声明一个数组来装到底选择了哪些商品 true 或者 false
        boolean[] isAdd = new boolean[goodsNums + 1];

        // 先处理0个商品和0容量的情况
        for(int i=0;i<packageCapcity+1;i++){
            tempArr[0][i] = 0;  // 将第一行置为0
        }
        for (int i=0;i<goodsNums+1;i++){
            tempArr[i][0] = 0;   // 将第一列置为0
        }

        // 如果第i个物品的重量大于了背包当前的剩余容量
        for (int i=1;i<goodsNums+1;i++){
            for (int j=1;j<packageCapcity+1;j++){
                // 开始判断
                if (goodsWeight[i-1]<=j){
                    // 可以装 ，但是可以选择不装，得判断   在装与不装之间取最大值来决定是否装
                    if (tempArr[i-1][j]<tempArr[i-1][j-goodsWeight[i-1]]+goodsValue[i-1]){
                        // 装
                        tempArr[i][j] = tempArr[i-1][j-goodsWeight[i-1]]+goodsValue[i-1];
                        //goodsFlag[i-1] = 1;
                    }else {
                        // 不装
                        tempArr[i][j] = tempArr[i-1][j];
                        //goodsFlag[i-1] = 0;
                    }
                }else {
                    // 不能装
                    tempArr[i][j] = tempArr[i-1][j];
                   // goodsFlag[i-1] = 0;
                }
            }
        }

        // 输出二维数组
        for (int i=0;i<goodsNums+1;i++){
            for (int j=0;j<packageCapcity+1;j++){
                System.out.print(tempArr[i][j]+" ");
            }
            System.out.println();
        }
        System.out.println("当前背包容量能装下的商品最大价值为："+tempArr[goodsNums][packageCapcity]);


        // 求解二维数组中最大价值是由哪些商品组成的
        for(int i = goodsNums; i >= 1; i--) {
            if(tempArr[i][packageCapcity] == tempArr[i-1][packageCapcity])
                isAdd[i] = false;
            else {
                isAdd[i] = true;
                packageCapcity -= goodsWeight[i-1];  // 如果是被选中的，那么就减去那个选中的。注意商品重量的数组下标。
            }
        }

        System.out.println("true代表被选中，false代表没被选中");
        for(int i = 1; i <= goodsNums; i++) {
            System.out.print(isAdd[i] + " ");
        }
        System.out.println();

    }
}