
制作于2017.6.13>>>16:44~17:37


这是「60天60个logo」的第十六天。
严格意义上来说,今天弄的这个算不上莫比乌斯环。
而这个莫比乌斯搞出来的东西确切来说应该叫「莫比乌斯带」
公元1858年,德国数学家莫比乌斯(Mobius,1790~1868)和约翰·李斯丁发现:把一根纸条扭转180°后,两头再粘接起来做成的纸带圈,具有魔术般的性质。普通纸带具有两个面(即双侧曲面),一个正面,一个反面,两个面可以涂成不同的颜色;而这样的纸带只有一个面(即单侧曲面),一只小虫可以爬遍整个曲面而不必跨过它的边缘。这种纸带被称为“莫比乌斯带”。(也就是说,它的曲面只有一个)

这次做出来的感觉是个三棱柱扭曲而成的??
为了验证自己的这个猜想,拿自己的橡皮实验了一波。

呃......应该......差不多??
构思阶段
感觉上面已经说完了吧。
元件制作
下面这波可能算是我至今做的最详细的一次过程说明了

先画一个椭圆

旁边再画一个
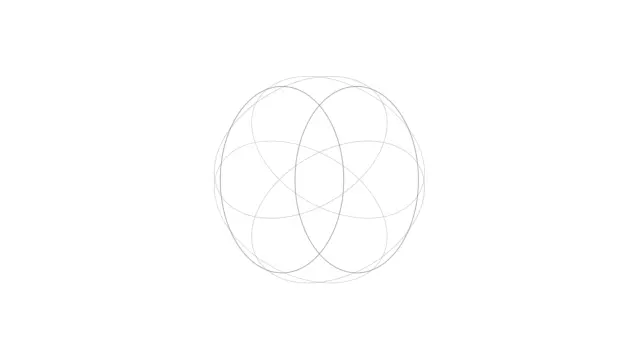
上面的图形组合复制两组,分别顺时针旋转60度、120度

保留这两个椭圆
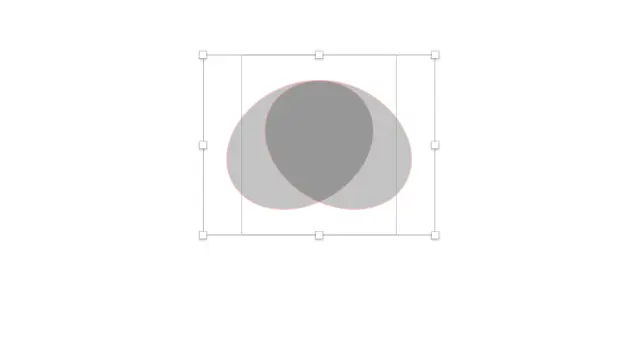
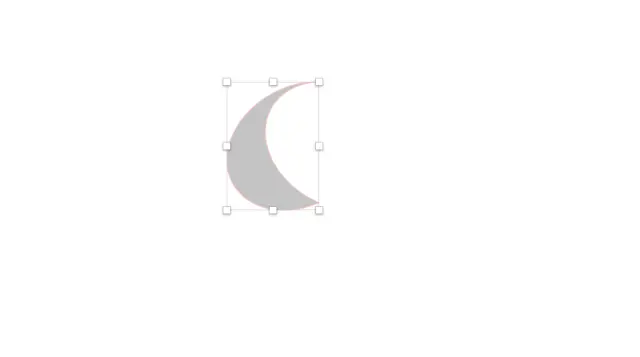
利用布尔运算,减去顶层

该月牙状图形复制六次,依次旋转60度、120度、180度、240度、300度。组合成这样的图形。
收工打卡

配个色就完事了。话说这个配色和昨天那么相近真的好吗????
作品列表
















小结
机智的您一定发现了,这样的设计方法可以衍生出各种扭曲状态。相关的旋转度数形状规范,自己慢慢摸索啦。反正这回受限于时间也来不及做了orz
至于下面这个......

说实话,做出这样的才是我真正的理想啊
(;´༎ຶД༎ຶ`)





 本文记录了作者使用椭圆通过布尔运算等步骤创建一个类似莫比乌斯带的三维立体Logo的过程,并探讨了其背后的几何原理。
本文记录了作者使用椭圆通过布尔运算等步骤创建一个类似莫比乌斯带的三维立体Logo的过程,并探讨了其背后的几何原理。
















 5232
5232

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








