关于反向传播

本文的$\theta$和$w$都表示权重，$\sigma$、$h_{\Theta }$和$g$都表示激活函数。

神经网络的代价函数：

$$\begin{array}{rl}J(\Theta )=& -\frac{1}{m}\left[\sum _{i=1}^m\sum _{k=1}^K{y}_k^{(i)}\log {\left(h_{\Theta }\left(x^{(i)}\right)\right)}_k+\left(1-y_k^{(i)}\right)\log \left(1-{\left(h_{\Theta }\left(x^{(i)}\right)\right)}_k\right)\right]\\ & +\frac{\lambda }{2m}\sum _{l=1}^{L-1}\sum _{i=1}^{s_l}\sum _{j=1}^{s_{l+1}}{\left({\Theta }_{ji}^{(l)}\right)}^2\end{array}$$

目标：

$$\underset{\Theta }{\min }J(\Theta )$$

需要计算：

$$J(\Theta )$$

$$\frac{\partial }{\partial {\Theta }_{ij}^{(l)}}J(\Theta )$$

假设只有一个训练样本（x，y），

神经网络结构如图：

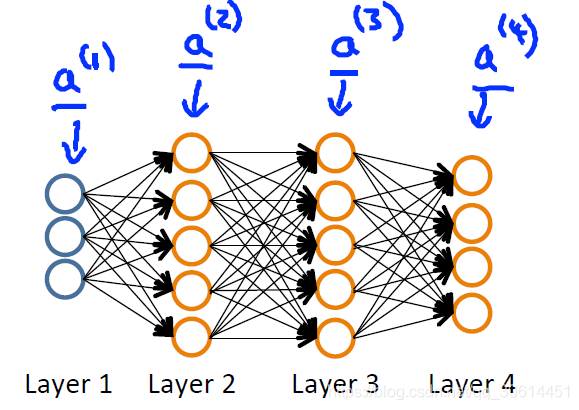
它的前向传播过程如下：
$$\begin{array}{l}{a}^{(1)}=x\\ z^{(2)}={\Theta }^{(1)}{a}^{(1)}\\ a^{(2)}=g\left(z^{(2)}\right)\left(\text{ add }{a}_0^{(2)}\right)\\ z^{(3)}={\Theta }^{(2)}{a}^{(2)}\\ a^{(3)}=g\left(z^{(3)}\right)\left(\text{ add }{a}_0^{(3)}\right)\\ z^{(4)}={\Theta }^{(3)}{a}^{(3)}\\ a^{(4)}=h_{\Theta }(x)=g\left(z^{(4)}\right)\end{array}$$

反向传播

${\delta }_j^{(l)}$ 表示L层j节点处的误差。
对上述一个4层的网络，
反向传播过程中，误差沿着反向传播如下，（公式推导见附录）：
$${\delta }_j^{(4)}=a_j^{(4)}-y_j$$

$$\begin{array}{l}{\delta }^{(3)}={\left({\Theta }^{(3)}\right)}^T{\delta }^{(4)}\cdot \ast g^{\prime }\left(z^{(3)}\right)\\ {\delta }^{(2)}={\left({\Theta }^{(2)}\right)}^T{\delta }^{(3)}\cdot \ast g^{\prime }\left(z^{(2)}\right)\end{array}$$

其中，$g^{\prime }\left(z^{}\right)=a^{}\cdot \ast \left(1-a^{}\right)$
表示sigmoid函数的导数。

这里的${\delta }_j^{(l)}$其实就是代价函数对$z_j^{(l)}$的偏导，可以对代价函数公式求偏导即可得证。
${\delta }_j^{(l)}=\frac{\partial }{\partial z_j^{(l)}}\mathrm{cost}(\mathrm{i})$
其中，单个样品的代价函数表示如下：
$\mathrm{cost}(\mathrm{i})=y^{(i)}\log h_{\Theta }\left(x^{(i)}\right)+\left(1-y^{(i)}\right)\log h_{\Theta }\left(x^{(i)}\right)$
其中，$h_{\Theta }\left(x^{(i)}\right)=a$，表示每一层的输出，$h_{\Theta }$就是sigmoid激活函数，与前文的g()一样。

误差函数对权重 ${\theta }_{ij}^{(l)}$的导数如下：
$$\frac{\partial }{\partial {\theta }_{ij}^{(l)}}J(\Theta )=a_j^{(l)}{\delta }_i^{(l+1)}$$

这个式子忽略正则项，$\lambda$为0.

对多个样本如何进行反向传播算法？

对训练集 $\left\{\left(x^{(1)},y^{(1)}\right),\dots ,\left(x^{(m)},y^{(m)}\right)\right\}$，
训练过程如下：
首先，置${△}_{ij}^{(l)}=0(\text{ for all }l,i,j)$

接着，遍历训练集：

For $i=1$ to $m$
{
令 $a^{(1)}=x^{(i)}$
通过前向传播计算 $a^{(l)}$ for $l=2,3,\dots ,L$
使用 $y^{(i)},$ 计算误差 ${\delta }^{(L)}=a^{(L)}-y^{(i)}$
通过反向传播计算每一层的误差， ${\delta }^{(L-1)},{\delta }^{(L-2)},\dots ,{\delta }^{(2)}$
${△}_{ij}^{(l)}:={△}_{ij}^{(l)}+a_j^{(l)}{\delta }_i^{(l+1)}$
}
计算完之后，跳出循环，计算下式：
$$\begin{array}{ll}{D}_{ij}^{(l)}:=\frac{1}{m}{△}_{ij}^{(l)}+\lambda {\Theta }_{ij}^{(l)}\text{ if }j̸=0& \\ D_{ij}^{(l)}:=\frac{1}{m}{△}_{ij}^{(l)}& \text{ if }j=0\end{array}$$
就可以得到偏导数：
$$\frac{\partial }{\partial {\Theta }_{ij}^{(l)}}J(\Theta )=D_{ij}^{(l)}$$

参考自：吴恩达机器学习视频

下面整理一下反向传播的过程：

第一步：输入训练集；

第二步：对于训练集中的每个样本x，设置输入层（Input layer）对应的激活值$a^1$：

第三步：前向传播：

$z^l=w^l{a}^{l-1}+b^l,a^l=\sigma \left(z^l\right)$

第四步: 计算输出层产生的错误：

${\delta }^L={\nabla }_{a}C\odot {\sigma }^{\prime }\left(z^L\right)$
也可以表示为：${\delta }^L=a_j-y_j$

第五步: 反向传播计算每一层的错误：

${\delta }^l=\left({\left(w^{l+1}\right)}^T{\delta }^{l+1}\right)\odot {\sigma }^{\prime }\left(z^l\right)$

第六步: 使用梯度下降（gradient descent），训练参数：

$w^l\to w^l-\frac{\eta }{m}{\sum }_x{\delta }^{x,l}{\left(a^{x,l-1}\right)}^T$
$b^l\to b^l-\frac{\eta }{m}{\sum }_x{\delta }^{x,l}$

附录

符号说明：
$w_{jk}^l$表示第l-1层的第k个神经元连接到第l层的第j个神经元之间的权重；
$b_j^l$表示第l层的第j个神经元的偏置；
$z_j^l$表示第l层的第j个神经元的输入，即：
$z_j^l={\sum }_k{w}_{jk}^l{a}_k^{l-1}+b_j^l$
$a_j^l$表示第l层第j个神经元的输出，即：
$a_j^l=\sigma \left({\sum }_k{w}_{jk}^l{a}_k^{l-1}+b_j^l\right)$
$\sigma$表示激活函数。（本文激活函数用不同的符号都表示过，但其实是一样的，从很多地方整理而来，懒得去改了）
$\odot$表示Hadamard乘积，用于矩阵或向量之间点对点的乘法运算.

误差的推导：

${\delta }^l=\left({\left(w^{l+1}\right)}^T{\delta }^{l+1}\right)\odot {\sigma }^{\prime }\left(z^l\right)$
推导过程：
$\because {\delta }_j^l=\frac{\partial C}{\partial z_j^l}={\sum }_k\frac{\partial C}{\partial z_k^{l+1}}\cdot \frac{\partial z_k^{l+1}}{\partial a_j^l}\cdot \frac{\partial a_j^l}{\partial z_j^l}$
$={\sum }_k{\delta }_k^{l+1}\cdot \frac{\partial \left(w_{kj}^{l+1}{a}_j^l+b_k^{l+1}\right)}{\partial a_j^l}\cdot {\sigma }^{\prime }\left(z_j^l\right)$
$={\sum }_k{\delta }_k^{l+1}\cdot w_{kj}^{l+1}\cdot {\sigma }^{\prime }\left(z_j^l\right)$
$\therefore {\delta }^l=\left({\left(w^{l+1}\right)}^T{\delta }^{l+1}\right)\odot {\sigma }^{\prime }\left(z^l\right)$

权重导数的推导：

$\frac{\partial C}{\partial w_{jk}^l}=a_k^{l-1}{\delta }_j^l$
推导过程：
$\frac{\partial C}{\partial w_{jk}^l}=\frac{\partial C}{\partial z_j^l}\cdot \frac{\partial z_j^l}{\partial w_{jk}^l}={\delta }_j^l\cdot \frac{\partial \left(w_{jk}^l{a}_k^{l-1}+b_j^l\right)}{\partial w_{jk}^l}=a_k^{l-1}{\delta }_j^l$

偏置导数的推导：

$\frac{\partial C}{\partial b_j^l}={\delta }_j^l$
推导过程：
$\frac{\partial C}{\partial b_j^l}=\frac{\partial C}{\partial z_j^l}\cdot \frac{\partial z_j^l}{\partial b_j^l}={\delta }_j^l\cdot \frac{\partial \left(w_{jk}^l{a}_k^{l-1}+b_j^l\right)}{\partial b_j^l}={\delta }_j^l$