视线估计、凝视目标估计相关评价指标

种蘑菇的金克斯

已于 2022-10-17 22:27:57 修改

阅读量1.3k

点赞数 2

文章标签：计算机视觉人工智能深度学习

于 2022-10-17 22:27:01 首次发布

本文链接：https://blog.youkuaiyun.com/qq_30540391/article/details/127331716

版权

1.TP、TN、FP、FN
$\qquad$ T、F表示待分类目标的GT值
$\qquad$ P、N表示预测到目标的正反例
在这里插入图片描述在目标检测类任务中：
$\qquad$ TP：表示正确检测到待检测目标
$\qquad$ TN：表示没有检测到待检测目标
$\qquad$ FP：表示预测到了非检测目标
$\qquad$ FN：表示没有检测到非监测目标（没有目标也没有检测到目标）
$\qquad$ 参考链接：https://blog.youkuaiyun.com/dongjinkun/article/details/109899733’

2.精确率（Precision）、召回率（Recall）、准确率（Accuracy）
$\qquad$ 原文链接：https://blog.youkuaiyun.com/littlehaes/article/details/83278256
$\qquad$ 准确率(Accuracy):这三个指标里最直观的就是准确率: 模型判断正确的数据(TP+TN)占总数据的比例

在这里插入图片描述

$\qquad$ 召回率(Recall): 针对数据集中的所有正例(TP+FN)而言,模型正确判断出的正例(TP)占数据集中所有正例的比例.FN表示被模型误认为是负例但实际是正例的数据.召回率也叫查全率,以物体检测为例,我们往往把图片中的物体作为正例,此时召回率高代表着模型可以找出图片中更多的物体!

在这里插入图片描述

$\qquad$ 精确率(Precision):针对模型判断出的所有正例(TP+FP)而言,其中真正例(TP)占的比例.精确率也叫查准率,还是以物体检测为例,精确率高表示模型检测出的物体中大部分确实是物体,只有少量不是物体的对象被当成物体

在这里插入图片描述
$\qquad$ 区分好召回率和精确率的关键在于:针对的数据不同,召回率针对的是数据集中的所有正例,精确率针对的是模型判断出的所有正例

3.角度误差
$\qquad$ 在模型估计出 pitch 角和 yaw 角之后，可以计算出代表视线方向的三维向量，该向量与真实的方向向量（ground truth）之间的夹角即是 gaze 领域最常用的评价指标。

$\qquad$ 图片链接：https://blog.youkuaiyun.com/c9Yv2cf9I06K2A9E/article/details/105400845

4.PR曲线、AUC指标
$\qquad$ 参考链接：https://blog.youkuaiyun.com/weixin_37817275/article/details/115859550
$\qquad$ PR曲线中的P代表的是precision（精准率），R代表的是recall（召回率），其代表的是精准率与召回率的关系，一般情况下，将recall设置为横坐标，precision设置为纵坐标。
在这里插入图片描述

$\qquad$ 1. 如果一条曲线完全“包住”另一条曲线，则前者性能优于另一条曲线。
$\qquad$ 2. PR曲线发生了交叉时：以PR曲线下的面积作为衡量指标，但这个指标通常难以计算。
$\qquad$ 3. 使用 “平衡点”（Break-Even Point），他是查准率=查全率时的取值，值越大代表效果越优
5.ROC
$\qquad$ 更多详细介绍参考链接：https://blog.youkuaiyun.com/weixin_37817275/article/details/115859550
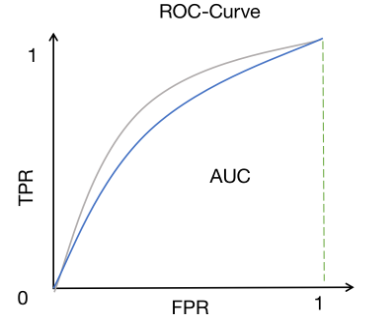
$\qquad$ ROC曲线的横坐标为FPR，纵坐标为TPR
$\qquad$ 1.将预测结果按照预测为正类概率值排序
$\qquad$ 2.将阈值由1开始逐渐降低，按此顺序逐个把样本作为正例进行预测，每次可以计算出当前的FPR，TPR值
$\qquad$ 3.以TPR为纵坐标，FPR为横坐标绘制图像
在这里插入图片描述
$\qquad$ ROC曲线下的面积（AUC）作为衡量指标，面积越大，性能越好。该指标经常被用来评价注视目标估计网络的性能。
6.欧氏距离（Dist.）
$\qquad$ 最常见的两点之间或多点之间的距离表示法，又称之为欧几里得度量，它定义于欧几里得空间中，如点 $x = ({x_1},...,{x_n})$ 和 $y = ({y_1},...,{y_n})$ 之间的距离为：
$\sqrt {{{\left( {{x_1} - {y_1}} \right)}^2} + {{\left( {{x_2} - {y_2}} \right)}^2} + \ldots + {{\left( {{x_n} - {y_n}} \right)}^2}} = \sqrt {\sum\limits_{i = 1}^n {{{\left( {{x_i} - {y_i}} \right)}^2}} }$
1.二维平面上两点 $a({x_1},{y_1})$ 与 $b({x_2},{y_2})$ 间的欧氏距离：
${{\rm{d}}_{12}} = \sqrt {{{\left( {{{\rm{x}}_1} - {{\rm{x}}_2}} \right)}^2} + {{\left( {{{\rm{y}}_1} - {{\rm{y}}_2}} \right)}^2}}$
2.两个n维向量 ${\rm{a}}\left( {{{\rm{x}}_{11}},{{\rm{x}}_{12}}, \ldots ,{{\rm{x}}_{1{\rm{n}}}}} \right)$ 与 $b\left( {{{\rm{x}}_{21}},{{\rm{x}}_{22}}, \ldots ,{{\rm{x}}_{{\rm{2n}}}}} \right)$ 间的距离：
${{\rm{d}}_{12}} = \sqrt {\sum\limits_{{\rm{k}} = 1}^{\rm{n}} {{{\left( {{{\rm{x}}_{1{\rm{k}}}} - {{\rm{x}}_{2{\rm{k}}}}} \right)}^2}} }$