AcWing 131 直方图中最大的矩形

题目描述：

直方图是由在公共基线处对齐的一系列矩形组成的多边形。矩形具有相等的宽度，但可以具有不同的高度。

例如，图例左侧显示了由高度为2,1,4,5,1,3,3的矩形组成的直方图，矩形的宽度都为1：

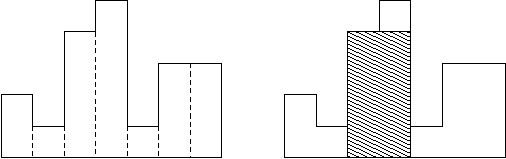
通常，直方图用于表示离散分布，例如，文本中字符的频率。现在，请你计算在公共基线处对齐的直方图中最大矩形的面积。

图例右图显示了所描绘直方图的最大对齐矩形。

输入格式

输入包含几个测试用例。每个测试用例占据一行，用以描述一个直方图，并以整数n开始，表示组成直方图的矩形数目。然后跟随n个整数h1，…，hn。这些数字以从左到右的顺序表示直方图的各个矩形的高度。每个矩形的宽度为1。同行数字用空格隔开。当输入用例为n=0时，结束输入，且该用例不用考虑。

输出格式

对于每一个测试用例，输出一个整数，代表指定直方图中最大矩形的区域面积。每个数据占一行。

请注意，此矩形必须在公共基线处对齐。

数据范围

1≤n≤100000,0≤hi≤1000000000

输入样例：

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

输出样例：

8
4000

分析：

观察题意，可以得出几个结论。其一，以矩形i的高度h[i]作为对齐矩形的高度想要得到最大的对齐矩形面积，当且仅当对齐矩形的宽度最大，即第i个矩形向左向右延伸到小于它高度的矩形为止（此时的对齐矩形不包括小于它高度的矩形）。其二，我们遍历一下所有以h[i]为高度的矩形的最大面积找出最大者即可得到最大矩形的面积。

所以，我们的目的就是高效的找到某矩形左边和右边离它最近的且高度小于它的矩形的位置。假设直方图中有连续的矩形abcde，h[a] > h[b]，则b后面的矩形（比如c）在向前找离它最近的高度小于它矩形的位置时，永远不会考虑a。因为一旦h[a] < h[c],必定有h[b] < h[c]，则c在向左遍历到b就会终止。可以得出：一旦出现了某个矩形比前面矩形矮，前面矩形的高度便没有多大用处了，所以需要保存的矩形必定是高度递增的一个矩形序列。而且该序列只会在一端插入和删除，由此想到使用单调栈。

方法一：直接通过单调栈的维持来找出每个矩形要找到的左右两边比它矮的最近的矩形位置。

设矩形i要找的左边高度小于它最近的位置是l[i],右边要找的位置是r[i]。首先考虑边界情况，对于直方图中高度最低的矩形，它的L是多少？引入哨兵结点0，使得h[0] = -1,于是0就是要找的L。同理对于最高的矩形，其R是n+1，右哨兵结点h[n+1] = -1。于是某矩形在向左找比它矮的矩形时，就算没有比它矮的矩形，也必然会终止于左哨兵结点，同理，向右查找的最坏情况也是终止于右哨兵结点。下面来描述下算法的执行流程：

首先左哨兵结点0入栈，之后每次遍历到一个矩形，是否要入栈则先进行判断。若该矩形高度大于栈顶矩形的高，则入栈，同时将该矩形的L置为栈顶元素的位置；若遍历到的矩形的高度小于栈顶元素的高度，则将栈顶元素的R置为当前矩形的位置，同时出栈，重复该过程，直至当前矩形的高度不小于栈顶矩形的高度为止。当然还需要考虑当前矩形的高度等于栈顶矩形高度的情况，此时，由于栈顶矩形的L在入栈时已经确定了，直接将其L赋给当前矩形的L即可。因此，所有的矩形都在入栈时L被赋值，出栈时R被赋值，直到遍历到右哨兵结点，不大于栈中所有元素，栈中的剩下元素再依次出栈。

对于矩形i，知道了其L[i]和R[i],（R[i] - L[i] - 1）* h[i]便是以h[i]为对齐矩形的高能够得到的最大矩形面积了。

#include <iostream>
#include <algorithm>
#include <stack>
using namespace std;
typedef long long ll;
const int maxn = 100005;
int n;
ll h[maxn];
int l[maxn],r[maxn];
int main(){
    while(cin>>n,n){
        ll ans = 0;
        stack<int> s;
        for(int i = 1;i <= n;i++)    cin>>h[i];
        h[0] = -1,h[n + 1] = -1;
        s.push(0);
        for(int i = 1;i <= n + 1;i++){
            if(h[i] > h[s.top()]){
                l[i] = s.top();
                s.push(i);
            }
            else if(h[i] == h[s.top()]){
                l[i] = l[s.top()];
                s.push(i);
            }
            else{
                while(h[i] < h[s.top()]){
                    r[s.top()] = i;
                    s.pop();
                }
                if(h[i] == h[s.top()]) l[i] = l[s.top()];
                else    l[i] = s.top();
                s.push(i);
            }
        }
        for(int i = 1;i <= n;i++)   ans = max(ans,h[i] * (r[i] - l[i] - 1));
        cout<<ans<<endl;
    }
    return 0;
}

方法二：维持一个矩形宽度数组来代替L,R数组。

可以发现，虽然方法一并不复杂，也是需要在纸上详细列出每种情况的处理办法才能够处理好本题的。我们知道，对于每个矩形，在入栈时，栈中元素均小于它，不会增加对齐矩形的宽度；当它出栈时，必然是遇见了R位置的矩形想要入栈，之后，它的宽度也不会增加。所以只需维持下各个矩形扩宽度时的宽度数组，便可知道以它为高矩形的最大宽度了。

具体表现为：扫描到某矩形，若其高度大于栈顶矩形的高度，则将其入栈，同时将其宽度置为一，表示不用向左延伸了。若其高度不大于栈顶元素，当其高度小于栈顶元素高度时，就到了栈顶元素出栈的时刻了，栈顶元素出栈，同时看能否更新ans。这里需要注意的是，每出栈一个元素，都需要将其宽度累加起来，有点类似于线段树的标记延迟下传，因为在每个元素入栈时，只是将该元素的宽度置为1，栈中元素的宽度其实也均要加一，之前未加，便要在元素出栈时将之前元素遗留下的宽度累加到新的栈顶元素的宽度上。

#include <iostream>
#include <algorithm>
#include <cstring>
#include <stack>
using namespace std;
typedef long long ll;
const int maxn = 100005;
int n;
ll h[maxn];
int wid[maxn];
int main(){
    while(cin>>n,n){
        ll ans = 0;
        stack<int> s;
        for(int i = 1;i <= n;i++)    cin>>h[i];
        h[0] = -1,h[n + 1] = -1;
        s.push(0);
        memset(wid,0,sizeof(wid));
        for(int i = 1;i <= n + 1;i++){
            if(h[i] > h[s.top()]){//大于栈顶元素时
                s.push(i);
                wid[i] = 1;
            }
            else{
                int w = 0;
                while(h[i] < h[s.top()]){
                    w += wid[s.top()];
                    ans = max(ans,h[s.top()] * w);
                    s.pop();
                }
                s.push(i);
                wid[i] = 1 + w;//相等和小于栈顶元素时
            }
        }
        cout<<ans<<endl;
    }
    return 0;
}