二叉树

本文里面的树的深度和高度的基数为1，但是有的地方是以0为基数的。两者都可以，重要是理解这种结构。

1.二叉树的定义

二叉树指的是每个树最多只能有两个子树的树形结构，也可以说成每个节点最多可以有两个子节点的树形结构。

2.二叉树的基本性质

1. 深度为n的节点的数目最多为$2^{n-1}$
2. 如果一棵树的深度为n,那么总的节点个数最多为$2^n+1$
3. 如果一棵树的总结点的数目为n，那么树的深度至少为$lo{g}_{2}n-1$
4. 在一颗二叉树中，如果度为0的节点的个数为$n_0$,度为2的节点的个数为$n_2$,那么存在关系$n_0$=$n_2$+1;
   推导的方式，因为树里面根节点的个数为1，假设总的节点的个数为n，度为1的节点的个数为$n_1$
   那么存在n=$n_1$+$n_2$+$n_0$;
   如果根据孩子节点推理：
   0度节点没有孩子节点，1度节点1个孩子节点，2度节点有两个孩子节点。并且根节点不属于任何节点的孩子节点。
   那么存在n=$n_1$+$n_2$*2+1;
   公式1和公式2相减就可以得到上面的等式。

3.二叉树的三种状态

1. 满二叉树 指的是深度为h的树的节点数目为$2^h-1$的二叉树
2. 完全二叉树 指的是只有最后一层或者倒数第二层存在度小于2的节点，并且最下一层的叶子节点的都集中分布在根节点的左侧。
3. 搜索二叉树 指的是一个节点如存在左子节点，那么左子节点的值一定小于父节点。如果存在右子节点，那么右子节点的值一定大于父节点。并且搜索二叉树里面不存在值相等的节点。

4.对二叉树遍历的三种方式

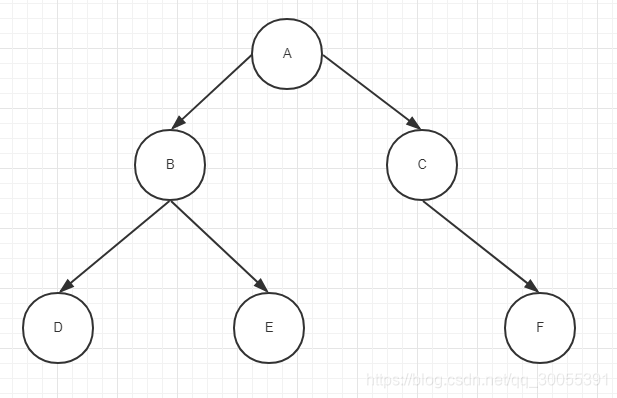
1. 前序遍历
   前序遍历的顺序是先根节点，然后左子树的节点，然后右子树的节点。同深度下并且属于同一个父节点的子节点，先遍历左边的节点，再遍历右边的节点。上面的图使用前序遍历的结果是ABDECF
2. 中序遍历 转自 https://blog.youkuaiyun.com/qq_33243189/article/details/80222629#commentBox

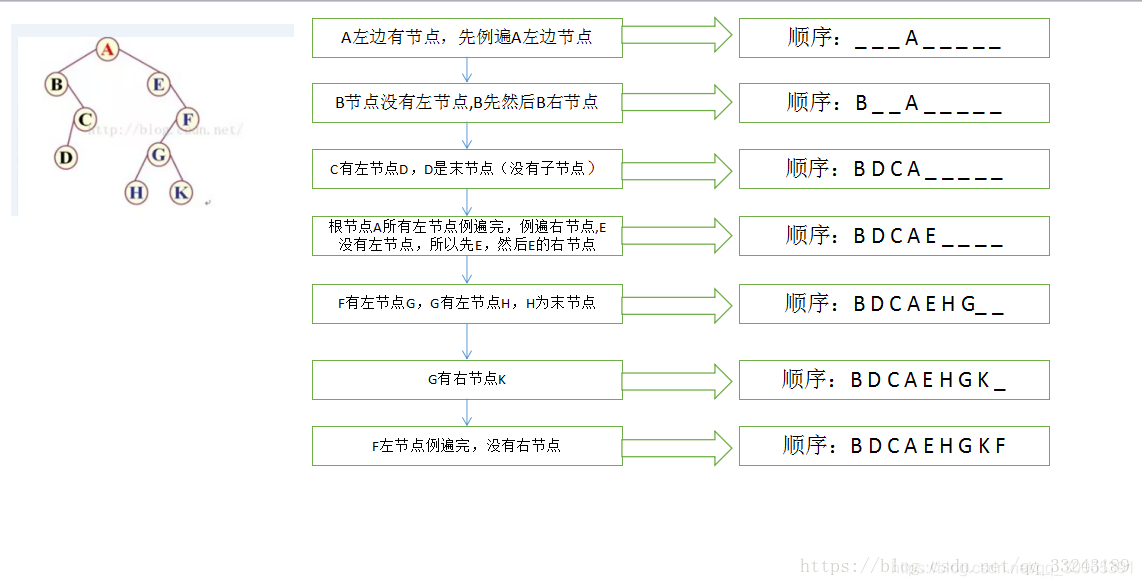
3. 后序遍历
   指的是先左后右最后根节点的遍历顺序。
   上面的图使用后序遍历的结果就是DEBFCA.