分门别类刷leetcode——动态规划（C++实现）

于 2019-01-26 18:22:51 发布
阅读量853 收藏 6
点赞数 2
CC 4.0 BY-SA版权
分类专栏： 刷题
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_29996285/article/details/86657638
本文精选LeetCode上经典的动态规划题目，深入解析包括爬楼梯、打家劫舍、最大子序和等题目的解题思路，阐述动态规划的四步法，即确认原问题和子问题、状态、边界条件及状态转移方程。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

目录

leetcode 70 爬楼梯

leetcode 198 打家劫舍

leetcode 53 最大子序和

leetcode 322 零钱兑换

leetcode 120 三角形最小路径和

leetcode 300 最长上升子序列

leetcode 64 不同路径

leetcode 174 地下城游戏

leetcode 304 二维区域和检索 - 矩阵不可变（2021 03 02）

leetcode 70 爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶

示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

思路：

暴力解法：

int climbStairs(int n) {
	if (n == 1 || n == 2) {
		return n;
	}
	return climbStairs(n - 1) + climbStairs(n - 2);
}

眼熟吗？这就是费波纳茨。动态规划的优点是把原问题划分成子问题，将每次子问题的计算结果都进行记录，通过查询记录避免了重复计算。

通过暴力搜索，可以推到出动态法规的递推公式：

第 i 阶楼梯爬法的数量 = 第 i -1 阶楼梯爬法的数量 + 第 i -2 阶楼梯爬法的数量

因此可以利用数组记录每一阶台阶的爬法，每次爬的时候，通过查询数组中的数据就可以获得结果。

 

动态规划的解析原理

通过上面的分析可知，动态规划的解题分为四步

1、确认原问题和子问题

  • 原问题——求n阶台阶所有走法的数量
  • 子问题——第 i 阶台阶走法的数量

2、确认状态

  • 本题的动态规划状态单一，第 i 个状态即为 i 台阶的所有走法数量

3、确认边界条件

  • 边界状态为第 1 阶台阶与第 2 阶台阶的走法。第一节台阶有一种走法，第二阶台阶有两种走法。

4、确认状态转移方程

  • 将第 i 个状态的值转移为求第 i-1 个状态值与第 i-2 个状态的值。动态规划状态转移方程为：dp[i]=dp[i-1]+dp[i-2]
class Solution {
public:
    int climbStairs(int n) {
        vector<int>dp(n+3,0);
        dp[1]=1;
        dp[2]=2;
        for(int i=3; i<=n; i++){
            dp[i]=dp[i-1]+dp[i-2];
        }
        return dp[n];
    }
};

 

 

 

leetcode 198 打家劫舍

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。

示例 1:

输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
     偷窃到的最高金额 = 1 + 3 = 4 。

示例 2:

输入: [2,7,9,3,1]
输出: 12
解释: 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
     偷窃到的最高金额 = 2 + 9 + 1 = 12 。

思考：

1、暴力枚举的方法

  • 对于每个房间，有两种可能：被盗和没被盗。如果采用暴力求解的方式，有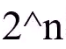种可能，时间复杂度是。

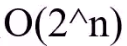2、贪心算法是否可行

  • 如果采用贪心算法，在满足不触发报警的同时，每次选择财宝最多的房间进行盗取，则贪心算法对于[5,2,6,3,1,7]的盗取结果是 7,6,5。

3、动态规划算法的原问题和子问题、状态、边界条件、状态转移方程如何确定？

 

思路：

对于房间 i 则：

  • 如果盗取 i 中的财宝，则不能盗取 i-1 号房间的财宝
  • 如果不盗取 i 中的财宝，则第 i-1 号房间的财宝可以选择盗取或者不盗取

 

动态规划的解析原理

通过上面的分析可知，动态规划的解题分为四步

1、确认原问题和子问题

  • 原问题——求n个房间的盗取财宝最优解
  • 子问题——第 i 个房间的盗取财宝最优解

2、确认状态

  • 第 i 个状态为前 i 个房间能够获得的最大财宝数。

3、确认边界条件

  • 前一个房间的最优解为盗取第一个房间的财宝
  • 前两个房间的最优解为盗取这两个房间中财宝最多的那个房间

4、确认状态转移方程

  • 盗取 i 房间：最优解为——第 i 个房间 + 前 i-2 个房间的最优解
  • 不盗取 i 房间：最优解为——第 i-1个房间的最优解

状态转移方程为：dp[i]=max(dp[i-1], dp[i-2]+nums[i]); (i>=3)

class Solution {
public:
    int rob(vector<int>& nums) {
        if(nums.size()==0) return 0;
        if(nums.size()==1) return nums[0];
        
        vector<int>dp(nums.size(), 0);
        dp[0]=nums[0];
        dp[1]=max(nums[0], nums[1]);
        for(int i=2; i<nums.size(); i++){
            dp[i]=max(dp[i-1], dp[i-2]+nums[i]);
        }
        return dp[nums.size()-1];
    }
};

 

 

 

leetcode 53 最大子序和

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

进阶:

如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。

思路：

将求n个数的数组的最大子段和，转换为分别求出以第 i 个、第 2 个、。。。、第 n 个数字结尾的最大子段和，再找出这 n 个结果中最大的，即为我们要的最终结果。

第 i 个状态（dp[i]）即为以第 i 个数字结尾的最大子段和。由于以第 i-1 个数字结尾的最大子段和 dp[i-1] 与 nums[i] 相邻：

  • 若dp[i-1]>0，则dp[i]=dp[i-1]+nums[i]
  • 否则，dp[i]=nums[i]

边界条件——dp[0]=nums[0]

因此推导出状态转移方程：dp[i]=max(dp[i-1]+nums[i], nums[i]);

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        vector<int>dp(nums.size(),0);
        dp[0]=nums[0];
        int max_res=dp[0];
        for(int i=1; i<nums.size(); i++){
            dp[i]=max(dp[i-1]+nums[i], nums[i]);
            if(max_res<dp[i]){
                max_res=dp[i];
            }
        }
        return max_res;
    }
};

 

 

 

leetcode 322 零钱兑换

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

示例 1:

输入: coins = [1, 2, 5], amount = 11

输出: 3
 
解释: 11 = 5 + 5 + 1

示例 2:

输入: coins = [2], amount = 3

输出: -1

思考——贪心算法是否可行？

对于钞票 [ 1, 2, 5, 10 ]，目标金额是14.最优解需要三张钞票

贪心思想——每次优先使用面值最大的，如：

现选一张10元的，剩下4元，再选一张2元的，剩下2元，再选一张2元的，搞定。

 

对于钞票 [ 1, 2, 5, 7, 10 ]，目标金额是14.最优解需要2张钞票

贪心思想——每次优先使用面值最大的，如：

现选一张10元的，剩下4元，再选一张2元的，剩下2元，再选一张2元的，钞票的使用张数超过了规定。

 

因此，贪心算法在个别面值组合时是可行的，但是本题的面值不确定，因此贪心思想不可行。需要使用动态规划来解决问题。

 

思路：

钞票 [ 1, 2, 5, 7, 10 ]，目标金额是14.

dp[i] 代表金额 i 的最优解（使用最小张数的解法）

数组dp[]中存储金额 1 至金额 14 的最优解。

 

在计算dp[i]时，dp[0], dp[1],...dp[i-1]都是已知的，而金额 i 可以由：

  • 金额 i-1 与 一张一块钱组合
  • 金额 i-2 与一张两块钱组合
  • 金额 i-5 与一张五块钱组合
  • 金额 i-7 与一张七块钱组合
  • 金额 i-10 与一张十块钱组合

因此，状态转移方程为：dp[i]=min(dp[i-1], dp[i-2], dp[i-5], dp[i-7], dp[i-10]) + 1

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        vector<int>dp(amount+1, -1);        
        
        dp[0]=0;
        for(int i=1; i<=amount; i++){
            for(int j=0; j<coins.size(); j++){
                if(i-coins[j]>=0 && dp[i-coins[j]]!=-1){
                    if(dp[i]==-1 || dp[i]>dp[i-coins[j]]+1){
                        dp[i]=dp[i-coins[j]]+1;
                    }
                }
            }
        }
        return dp[amount];
    }
};

 

 

 

leetcode 120 三角形最小路径和

给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。

例如，给定三角形：

[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

说明：

如果你可以只使用 O(n) 的额外空间（n 为三角形的总行数）来解决这个问题，那么你的算法会很加分。

思路：

class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) {
        if(triangle.empty()) return 0;
        
        vector<vector<int>>dp;
        for(int i=0; i<triangle.size(); i++){
            dp.push_back(vector<int>());
            for(int j=0; j<triangle[i].size(); j++){
                dp[i].push_back(0);
            }
        }
        //给最后一层赋值
        for(int i=0; i<dp[dp.size()-1].size(); i++){
            dp[dp.size()-1][i]=triangle[dp.size()-1][i];
        }
        //逐层向上赋值
        for(int i=dp.size()-2; i>=0; i--){
            for(int j=0; j<dp[i].size(); j++){
                dp[i][j]=min(dp[i+1][j], dp[i+1][j+1])+triangle[i][j];
            }
        }
        return dp[0][0];
    }
};

 

 

 

leetcode 300 最长上升子序列

给定一个无序的整数数组，找到其中最长上升子序列的长度。

示例:

输入: [10,9,2,5,3,7,101,18]
输出: 4 
解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。

说明:

  • 可能会有多种最长上升子序列的组合，你只需要输出对应的长度即可。
  • 你算法的时间复杂度应该为 O(n2) 。

进阶: 你能将算法的时间复杂度降低到 O(n log n) 吗?

思路：

方法一：

若第 i 个状态 dp[i] 代表以第 i 个元素结尾的最长上升子序列的长度：dp[i-1] 代表第 i-1 个元素结尾的最长上升子序列。。。。因此dp[n]为前面各个dp中的最大值。

用一个变量LIS来记录当前的最长上升子序列的长度。

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        if(nums.empty()) return 0;
        
        vector<int>dp(nums.size(), 0);
        dp[0]=1;
        int LIS=1;
        for(int i=1; i<dp.size(); i++){
            dp[i]=1;
            for(int j=0; j<i; j++){
                if(nums[i]>nums[j] && dp[i]<dp[j]+1){
                    dp[i]=dp[j]+1;
                }
            }
            if(LIS<dp[i]) LIS=dp[i];
        }
        return LIS;
    }
};

 

方法二：

使用栈思想（vector实现），从 1 到 n-1 遍历数组。

  • 若num[i]>栈顶，则将num[i]入栈
  • 若num[i]<栈顶，则遍历栈中元素，将栈中第一个大于等于nums[i]的元素的值修改为nums[i]。
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        if(nums.empty()) return 0;
        
        vector<int>stack;
        stack.push_back(nums[0]);
        for(int i=1; i<nums.size(); i++){
            if(nums[i]>stack.back())
                stack.push_back(nums[i]);
            else{
                for(int j=0; j<stack.size(); j++){
                    if(stack[j]>=nums[i]){
                        stack[j]=nums[i];
                        break;
                    }
                }
            }
        }
        return stack.size();
    }
};

 

优化方法二：

使用二分查找法查找栈中第一个大于等于 nums[i] 的值。从而降低时间复杂度为O(nlogn)。

class Solution {
public:
    int binary_search(vector<int>nums, int target){
        int index=-1;
        int begin=0;
        int end=nums.size()-1;
        while(index==-1){
            int mid=(begin+end)/2;
            if(target==nums[mid])
                index=mid;
            else if(target<nums[mid]){
                if(mid==0 || target>nums[mid-1])
                    index=mid;
                end=mid-1;
            }
            else if(target>nums[mid]){
                if(mid==nums.size()-1 || target<nums[mid+1])
                    index=mid+1;
                begin=mid+1;
            }
        }
        return index;
    }
    
    int lengthOfLIS(vector<int>& nums) {
        if(nums.empty()) return 0;
        
        vector<int>stack;
        stack.push_back(nums[0]);
        for(int i=1; i<nums.size(); i++){
            if(nums[i]>stack.back())
                stack.push_back(nums[i]);
            else{
                int pos=binary_search(stack, nums[i]);
                stack[pos]=nums[i];
            }
        }
        return stack.size();
    }
};

 

 

 

leetcode 64 不同路径

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例:

输入:
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。

思路：

开辟一个和输入的数组一样大的二维数组，从左上角开始，分别向右和向下走，用新开辟的数组记录每一步需要走的路径长度。

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        if((grid.size()<1)||(grid[0].size()<1)) return 0;
        
        vector<vector<int>>dp(grid.size(),vector<int>(grid[0].size()));
        
        dp[0][0]=grid[0][0];
        for(int i=1; i<grid[0].size(); i++){
            dp[0][i]=grid[0][i]+dp[0][i-1];
        }
        for(int i=1; i<grid.size(); i++){
            dp[i][0]=grid[i][0]+dp[i-1][0];
        }
        for(int i=1; i<grid.size(); i++){
            for(int j=1; j<grid[0].size(); j++){
                dp[i][j]=grid[i][j]+min(dp[i-1][j],dp[i][j-1]);
            }
        }
        return dp[grid.size()-1][grid[0].size()-1];
    }
};

 

 

 

leetcode 174 地下城游戏

一些恶魔抓住了公主（P）并将她关在了地下城的右下角。地下城是由 M x N 个房间组成的二维网格。我们英勇的骑士（K）最初被安置在左上角的房间里，他必须穿过地下城并通过对抗恶魔来拯救公主。

骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下，他会立即死亡。

有些房间由恶魔守卫，因此骑士在进入这些房间时会失去健康点数（若房间里的值为负整数，则表示骑士将损失健康点数）；其他房间要么是空的（房间里的值为 0），要么包含增加骑士健康点数的魔法球（若房间里的值为正整数，则表示骑士将增加健康点数）。

为了尽快到达公主，骑士决定每次只向右或向下移动一步。

 

编写一个函数来计算确保骑士能够拯救到公主所需的最低初始健康点数。

例如，考虑到如下布局的地下城，如果骑士遵循最佳路径 右 -> 右 -> 下 -> 下，则骑士的初始健康点数至少为 7。

骑士的健康点数没有上限。说明:

  • 任何房间都可能对骑士的健康点数造成威胁，也可能增加骑士的健康点数，包括骑士进入的左上角房间以及公主被监禁的右下角房间。

这题让我想起一首歌：达拉崩吧_在线试听_高音质歌曲_酷我音乐  

思路：

从左上到右下，还要保证骑士不死，初始血量是多少这个真不好定。我们从右下角出发吧~

从右下角到左上角，dp[i][j]代表要到达该点，至少需要多少血量。

例如:

  • 若地牢为 1*1 的矩阵，则dp[0][0]=max(1, 1-dungeon[0][0])

      

  • 若地牢为 1*n 的：dp[0][i] = max(1, dp[0][i+1] - dungeon[0][i] ) ;

     

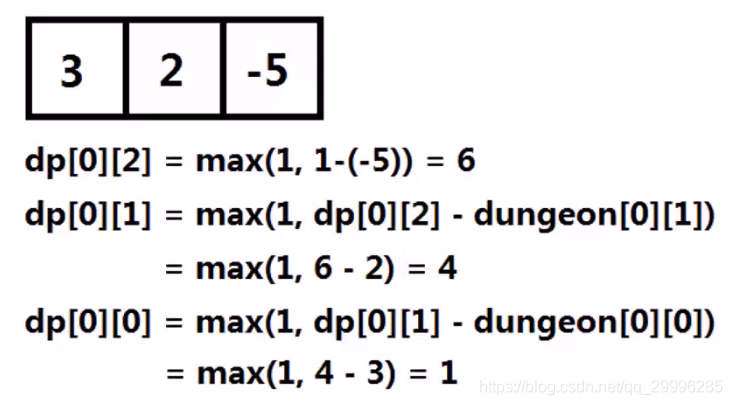
  • 若地牢为 n*1 的：dp[i][0] = max(1, dp[i+1][0] - dungeon[i][0] ) ;
  • 若地牢为 n*m 的数组，i 代表行， j 代表列设 dp_min=min(dp[ i+1 ][ j ], dp[ i ][ j+1 ]);，
  • 则 dp[ i ][ j ] = max( 1, dp_min - dungeon[ i ][ j ])
class Solution {
public:
    int calculateMinimumHP(vector<vector<int>>& dungeon) {
        if(dungeon.size()<1 || dungeon[0].size()<1) return 0;
        
        vector<vector<int>>dp(dungeon.size(), vector<int>(dungeon[0].size()));
        int row=dungeon.size();
        int column=dungeon[0].size();
        
        // 1*1 的矩阵情况
        dp[row-1][column-1]=max(1,1-dungeon[row-1][column-1]);
        
        for(int i=column-2; i>=0; i--){
            dp[row-1][i]=max(1, dp[row-1][i+1]-dungeon[row-1][i]);
        }
        
        // n*1
        for(int i=row-2; i>=0; i--){
            dp[i][column-1]=max(1, dp[i+1][column-1]-dungeon[i][column-1]);
        }
        
        // 1*n
        for(int i=column-2; i>=0; i--){
            dp[row-1][i]=max(1, dp[row-1][i+1]-dungeon[row-1][i]);
        }
        // n*m
        for(int i=row-2; i>=0; i--){
            for(int j=column-2; j>=0; j--){
                int dp_min=min(dp[i+1][j], dp[i][j+1]);
                dp[i][j]=max(1, dp_min-dungeon[i][j]);
            }
        }
        return dp[0][0];        
    }
};

 

 

 

 

leetcode 304 二维区域和检索 - 矩阵不可变（2021 03 02）

给定一个二维矩阵，计算其子矩形范围内元素的总和，该子矩阵的左上角为 (row1, col1) ，右下角为 (row2, col2)。

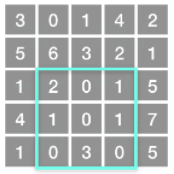
上图子矩阵左上角 (row1, col1) = (2, 1) ，右下角(row2, col2) = (4, 3)，该子矩形内元素的总和为 8。

示例:

给定 matrix = [
  [3, 0, 1, 4, 2],
  [5, 6, 3, 2, 1],
  [1, 2, 0, 1, 5],
  [4, 1, 0, 1, 7],
  [1, 0, 3, 0, 5]
]

sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12

说明:

  • 你可以假设矩阵不可变。
  • 会多次调用 sumRegion 方法。
  • 你可以假设 row1 ≤ row2 且 col1 ≤ col2。

思路：

使用动态规划法，分别计算出矩阵中各个点到左上角点位置的总和。求sumRegion时，将不需要的区域总和去掉即可。

答案

class NumMatrix {
private:
    vector<vector<int>> dp;

public:
    NumMatrix(vector<vector<int>> matrix) {
        if (matrix.size() == 0 || matrix[0].size() == 0) {
            return;
        }
        int n = matrix.size();
        int m = matrix[0].size();
        
        dp.resize(n + 1, vector<int>(m + 1, 0));
        for (int r = 0; r < n; r++) {
            for (int c = 0; c < m; c++) {
                dp[r + 1][c + 1] = dp[r + 1][c] + dp[r][c + 1] + matrix[r][c] - dp[r][c];
            }
        }
    }
    
    int sumRegion(int row1, int col1, int row2, int col2) {
        return dp[row2 + 1][col2 + 1] - dp[row1][col2 + 1] - dp[row2 + 1][col1] + dp[row1][col1];
    }
};

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix* obj = new NumMatrix(matrix);
 * int param_1 = obj->sumRegion(row1,col1,row2,col2);
 */

 

 

 

 

更多的动态规划问题（收录来自牛客网） 来啃硬骨头——c++ 动态规划

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值