最长公共子序列

最新推荐文章于 2022-11-15 14:20:36 发布

大道朝天

最新推荐文章于 2022-11-15 14:20:36 发布

阅读量103

点赞数

CC 4.0 BY-SA版权

本文链接：https://blog.youkuaiyun.com/qq_29869043/article/details/82724924

本文深入探讨了最长公共子序列(LCS)算法，详细解释了如何使用动态规划方法求解两个序列的最长公共子序列，并提供了完整的C++实现代码。通过理解LCS的概念和状态转移方程，读者可以掌握解决此类问题的技巧。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

最长公共子序列和最长公共子串不同，最长公共子序列可以在原序列中是不连续的，最长公共子串在原序列中必须是连续的

dp[i][j]数组代表长度为i的arr1 和长度为j的arr2 的最长公共子序列的长度

//dp的状态公式
if (arr1[i - 1] == arr2[j - 1])
{
    dp[i][j] = dp[i - 1][j - 1] + 1;
}
else
{
    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}

dp[i][j]的变化

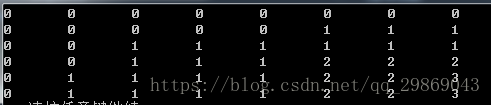
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
#include <stack>

using namespace std;

//最长公共子序列和最长公共子串不同，最长公共子序列可以在原序列中是不连续的， 最长公共子串在原序列中必须是连续的

vector<int> LongestCommonSequence(vector<int>& arr1, vector<int>& arr2)
{
	int length1 = arr1.size();
	int length2 = arr2.size();
	//dp[i][j]数组代表长度为i的arr1 和 长度为j的arr2 的最长公共子序列的长度
	//一开始初始化为0
	vector<vector<int>> dp(length1 + 1, vector<int>(length2 + 1, 0));
	//最长公共子序列序列
	vector<int> sub;
	for (int i = 1; i <= length1; ++i)
	{
		for (int j = 1; j <= length2; ++j)
		{
			if (arr1[i - 1] == arr2[j - 1])
			{
				dp[i][j] = dp[i - 1][j - 1] + 1;
			}
			else
			{
				dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
			}
		}
	}

	int i = length1, j = length2;
	while (i >= 1, j >= 1)
	{
		if (dp[i][j] == dp[i][j - 1])
		{
			--j;
		}
		else if (dp[i][j] == dp[i - 1][j])
		{
			--i;
		} 
		else
		{
			sub.push_back(arr1[i - 1]);
			--i;
			--j;
		}
	}
	reverse(sub.begin(), sub.end());
	return sub;
}

int main()
{
	vector<int> arr1 = { 3, 5, 3, 2, 8 };
	vector<int> arr2 = { 2, 5, 7, 9 ,3, 1, 2 };
	vector<int> sub(LongestCommonSequence(arr1, arr2));
	for (auto & it : sub)
		cout << it;
}