经济均衡问题及其应用 (二)：拍卖与投标问题_投标问题的线性规划-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_29831163/article/details/89403559

本文通过实例解析了艺术品拍卖中的清算价格确定问题，利用线性规划模型确定了每类艺术品的清算价格，确保了拍卖过程的公平性和效率。模型考虑了艺术品数量、投标人报价及购买限制，最终求解得到了最优分配方案和清算价格。

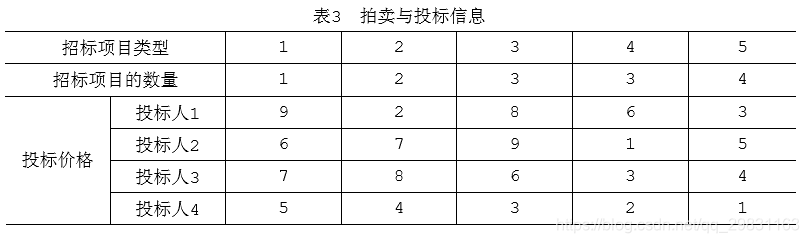
例3 假设一家拍卖行对委托的5类艺术品对外拍卖，采用在规定日期前投标人提交投标书的方式进行，最后收到了来自4个投标人的投标书。每类项目的数量、投标人对每个项目的投标价格如表3中所示。例如，有3件第4类艺术品；对每件第4类艺术品，投标人1，2，3愿意出的最高价分别为6，1，3，2（货币单位，如万元）。此外，假设每个投标人对每类艺术品多只能购买1件，并且每个投标人购买的艺术品的总数不能超过3件。那么，哪些艺术品能够卖出去？卖给谁？这个拍卖和投标问题中每类物品的清算价应该是多少？

（1）问题分析

这个具体问题在实际中可能可以通过对所有投标的报价进行排序来解决，例如可以总是将艺术品优先卖给出价高的投标人。但这种方法不太好确定每类艺术品的清算价，所以我们这里还是借用前面两个例子中的方法，即假设有一个中间商希望大化自己的利润，从而建立这个问题的线性规划模型。

（2）问题的一般提法和假设

先建立一般的模型，然后求解本例的具体问题，设有n类物品需要拍卖，第 j 类物品的数量为 $\tiny s_{j}$ （ j=1,2,...,n ）；有m 个投标者，投标者i（ i=1,2,...,m ）对第 j 类物品的投标价格为 $\tiny b_{ij}$ （假设非负）。投标者i对每类物品多购买一件，且总件数不能超过 $\tiny c_{i}$ 。我们的目标之一是要确定第 j 类物品的清算价格 $\tiny p_{j}$ ，它应当满足下列假设条件：

i）成交的第 j 类物品的数量不超过 $\tiny s_{j}$ （ j=1,2,...,n ）；

ii）对第 j 类物品的报价低于 $\tiny p_{j}$ 的投标人将不能获得第 j 类物品；

iii）如果成交的第 j 类物品的数量少于 $\tiny s_{j}$ （ j=1,2,...,n ）,可以认为 $\tiny p_{j}=0$ （除非拍卖方另外指定一个低的保护价）；

iv）对第 j 类物品的报价高于 $\tiny p_{j}$ 的投标人有权获得第 j 类物品，但如果他有权获得的物品超过3件，那么我们假设他总是希望使自己的满意度大（满意度可以用他的报价与市场清算价之差来衡量）。

（3）优化模型

用 0−1 变量 $\tiny x_{ij}$ 表示是否分配一件第 j 类物品给投标者i，即 $\tiny x_{ij}=1$ 表示分配，而 $\tiny x_{ij}=0$ 表示不分配。目标函数仍然是虚拟的中间商的总利润（认为这些利润全部是拍卖行的利润也可以），即

$\tiny \sum_{i=1}^{m}\sum_{j=1}^{n}b_{ij}x_{ij}$ （1）

除变量取值为0或1的约束外，问题的约束条件主要是两类：每类物品的数量限制和每个投标人所能分到的物品的数量限制，即
$\tiny \sum_{i=1}^{m}x_{ij} \leqslant s_{j}\: ,j=1,2,..,n$ （2）

$\tiny \sum_{j=1}^{n}x_{ij}\leqslant c_{i}\, ,i=1,2,..,m$ (3)

模型就是在约束（2）、（3）下最大化目标函数（1）。

（4）模型求解

编写的LINGO程序如下：

MODEL: 
TITLE 拍卖与投标; 
SETS:  
    AUCTION/1..5/: S;  
    BIDDER/1..4/ : C;  
    LINK(BIDDER,AUCTION): B, X; 
ENDSETS 
DATA:  
    S=1 2 3 3 4;  
    C=3 3 3 3;  
    B= 9 2 8 6 3 
       6 7 9 1 5 
       7 8 6 3 4 
       5 4 3 2 1 ; 
ENDDATA 
MAX=@SUM(LINK: B*X); 
@FOR(AUCTION(J):  
    [AUC_LIM] @SUM(BIDDER(I): X(I,J)) < S(J) ); 
@FOR(BIDDER(I): 
    [BID_LIM] @SUM(AUCTION(J): X(I,J)) < C(I) ); 
@FOR(LINK: @BND(0,X,1)); 
END

（5）求解结果解释

可以看到，优解为：

投标人1得到艺术品1，3，4，

投标人2，3都得到艺术品2， 3，5，

投标人4得到艺术品4，5。

结果，第4，5类艺术品各剩下1件没有成交。那么如何才能确定清算价格呢？与例1和例2类似，约束“AUC_LIM”是针对每类艺术品的数量限制的，对应的影子价格就是其清算价格：即5类艺术品的清算价格分别是5，5，3，0，0。第4，5类艺术品有剩余，所以清算价格为0，这是符合前面的假设的。

可以指出的是：即使上面模型中不要求 $\tiny x_{ij}$ 为 0−1 变量（即只要求取0～1之间的实数），由于这个问题的特殊性，优解中 $\tiny x_{ij}$ 也会要么取0，要么取1，不可能取0～1之间的其它数，所以可以将LINGO模型中“@BIN(X)”改为“@BND(0,X,1)”，这个线性规划的结果将与 0−1 整数线性规划得到的结果相同。

最后，大学生的选课问题与此是类似的，即把课程看成招标（拍卖）项目，而把学生愿意付出的选课费看成投标。据说国外有些大学的选课系统就是使用这个模型确定每门课程的清算价格（选课费用）的，而且取得了成功。