哈希表(理论剖析+代码实现)

哈希表

---

1.关联式容器与序列式容器的了解

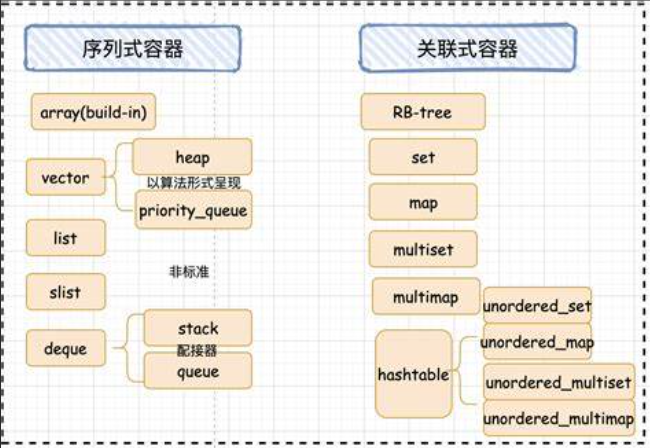
序列式容器：以线性风格存储给定类型对象的容器，可以作为动态数组或者列表，元素根据它们在容器中的位置来检索

关联式容器：为每个要存储对象的键存储对象，这些键用来定位容器内的对象

---

2.unordered系列关联式容器概念

1. 在C++98中，STL提供了底层为红黑树结构的一系列关联式容器，在查询时效率可达到 O(log2N)，即最差情况下需要比较红黑树的高度次，当树中的节点非常多时，查询效率也不理想
2. 最好的查询是，进行很少的比较次数就能够将元素找到
3. 因此在C++11中，STL又提供了4个 unordered 系列的关联式容器，这4个容器与红黑树结构的关联式容器底层结构不同，称为哈希表
4. 哈希其实就是一种散列、一种映射

哈希表结构的 unordered 系列的关联式容器与红黑树结构的关联式容器 map/set/multimap/multiset 使用方式上基本类似，它们的主要区别在于：

1. unordered 系列关联式容器，遍历出来不是有序的，迭代器是单向迭代器
2. unordered_map 和 unordered_set 不允许数据冗余，支持 [] 操作符
3. unordered_multimap 和 unordered_multiset 允许数据冗余，不支持 [] 操作符

---

3.unordered系列关联容器底层结构

unordered 系列的关联式容器之所以效率比较高，是因为其底层使用了哈希结构

举例：

// release下测试，debug下可能还会受限于编译器的优化程度，release下是最高优化
void test()
{
   
   
	// 用n个随机值元素来测试set和unordered_set

	// 定义容量为N的向量
	const int N = 1000000;
	vector<int> v;
	v.reserve(N);

	srand(time(0)); // 初始化随机种子

	for (size_t i = 0; i < N; i++)
	{
   
   
		v.push_back(rand()); // 插入生成的随机值
	}

	// 定义set和unordered_set
	set<int> s;
	unordered_set<int> us;

    /* ----------------------------------------------------------------- */
	// 向set中插入N个随机值，统计时间(ms)
	size_t begin1 = clock();
	for (auto& e : v)
	{
   
   
		s.insert(e);
	}
	size_t end1 = clock();

	// 向unordered_set插入N个随机值，统计时间(ms)
	size_t begin2 = clock();
	for (auto& e : v)
	{
   
   
		us.insert(e);
	}
	size_t end2 = clock();

	cout << "set - inset: " << end1 - begin1 << endl;
	cout << "unordered_set - inset: " << end2 - begin2 << endl;
    
    /* ----------------------------------------------------------------- */
	// 依次去set中查找向量中的N个元素，统计时间(ms)
	size_t begin3 = clock();
	for (auto& e : v)
	{
   
   
		s.find(e);
	}
	size_t end3 = clock();
	
	// 依次去unordered_set中查找向量中的N个元素，统计时间(ms)
	size_t begin4 = clock();
	for (auto& e : v)
	{
   
   
		us.find(e);
	}
	size_t end4 = clock();

	cout << "set - find(): " << end3 - begin3 << endl;
	cout << "unordered_set - find(): " << end4 - begin4 << endl;
	
    /* ----------------------------------------------------------------- */
	// 依次删除set中的N个元素，统计时间(ms)
	size_t begin5 = clock();
	for (auto& e : v)
	{
   
   
		s.erase(e);
	}
	size_t end5 = clock();

	// 依次删除unordered_set中的N个元素，统计时间(ms)
	size_t begin6 = clock();
	for (auto& e : v)
	{
   
   
		us.erase(e);
	}
	size_t end6 = clock();

	cout << "set - erase(): " << end5 - begin5 << endl;
	cout << "unordered_set - erase(): " << end6 - begin6 << endl;
}

用同一批100万个数据来测试 unordered_set 和 set，结果分析如下：

所以一般情况下，建议使用 unordered 系列的关联式容器

---

3.哈希的概念了解

• 在顺序结构以及平衡树中，元素关键码与其存储位置之间没有对应的关系，因此在查找一个元素时，必须要经过关键码的多次比较。顺序查找时间复杂度为O(N)，平衡树中为树的高度，即O(logN)，搜索的效率决于搜索过程中元素的比较次数
• 理想的搜索方法：可以不经过任何比较，一次直接从表中得到要搜索的元素。 如果构造一种存储结构，通过某种函数(hashFunc)使元素的存储位置与它的关键码之间能够建立一一映射的关系，那么在查找时通过该函数可以很快找到该元素
  
  

当向该结构中：

• 插入元素：根据待插入元素的关键码，以此函数计算出该元素的存储位置并按此位置进行存放
• 搜索元素：对元素的关键码进行同样的计算，把求得的函数值当做元素的存储位置，在结构中按此位置取元素比较，若关键码相等，则搜索成功
  
  

该方式即为哈希(散列)方法，哈希方法中使用的转换函数称为哈希(散列)函数，构造出来的结构称为哈希表(Hash Table)(或者称散列表)

---

4.哈希函数的了解

其实就是按照某种规则，给元素找一个存储位置（哈希位置、映射位置）

常见哈希函数：

1. 直接定址法（常用）

   1. 取关键字的某个线性函数为散列地址：Hash（Key）= A * Key + B
   2. 优点：简单、均匀
   3. 缺点：需要事先知道关键字的分布情况，如果关键字的分布比较分散，会很浪费空间
   4. 使用场景：适合查找比较小且连续的情况，比如：
      • 计数排序
      • 一些OJ题中用哈希映射来统计字符出现次数
      • 利用字符的ASCII码值来映射字符，利用int型变量的数值来映射该变量

2. 除留余数法（常用）

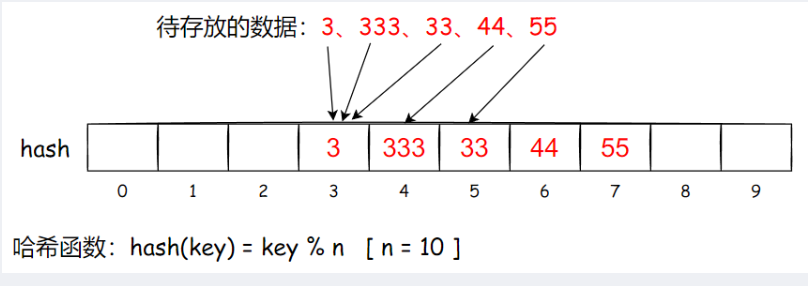
   1. 开一段固定大小的空间，比如哈希表中允许的地址数为 n，按照哈希函数：Hash(key) = key % n，得到的余数就是该关键码的哈希地址，存放到哈希表对应位置中

   2. 缺陷：

      • 适用于整数的存储（字符串、浮点数不能直接存储，因为不能直接取模，后面会讲如何解决）
      • 余数相同时，会出现哈希冲突

      比如：

   

---

5.哈希冲突的了解

1. 不同关键字通过相同哈希哈数计算出相同的哈希地址，映射到了相同位置，该种现象称为哈希冲突或哈希碰撞
2. 解决哈希冲突两种常见的方法是：闭散列和开散列

---

6.解决哈希冲突：闭散列

6.1 闭散列的概念了解

闭散列也叫开放定址法：

1. 开放寻址法的核心思想是，通过哈希函数计算出这个数据对应的哈希位置，如果该位置出现了哈希冲突，我们就重新探测一个空闲位置，将其插入。那如何重新探测新的位置呢？当我们往散列表中插入数据时，如果某个数据经过散列函数散列之后，存储位置已经被占用了，我们就从当前位置开始，依次往后查找，看是否有空闲位置，直到找到为止。如果数组整个都没有空位置，这个时候就需要对数组进行扩容操作

2. 而我们要获取数据的时候就需要先Hash运算，然后得到下标后再去拿值，拿到值后要比对是不是要拿的数据，因为有可能Hash冲突了，此时的值并不是你想要的，如果是就直接取出，不是的话就需要重新遍历数组，直到找到对应的数

3. 从上面可以明显的看出来开发寻址法并不是一种好的方案，当最好的情况时查询数据时间复杂度为O(1),而最坏的情况时就需要遍历整个数组从而退化为O(n)，平均时间复杂度为O(1)

---

6.2 闭散列探测空位置方法

当前哈希位置已经存放的有数据了，下一个元素也是映射的这个位置，发生哈希冲突了，那怎么办呢？

• 如果哈希表未被装满，说明在哈希表中必然还有空位置，那么可以把该元素存放到冲突位置的 “ 下一个空位置 ” 中去
• 如果整个数组都没有空位置了，这个时候就需要对数组进行扩容操作
  
  

找下一个空位置有两种方法：线性探测和二次线性探测

1.线性探测：从发生冲突的位置开始，依次向后探测，直到寻找到下一个空位置为止

1. 线性探测的优点：实现起来非常简单

2. 线性探测的缺陷：

   • 如果某个位置冲突的多，会导致一片冲突很多，数据堆积在一起

   • 插入和查找的效率都会降低很多，插入元素时，从冲突位置开始不断往后找到下一个空位置；查找元素时，从冲突位置开始不断往后找，需要比较许多次，导致搜索效率降低。最坏情况下要直到找到空位置时，才能说明没有该元素

   • 比如下图：

观察发现，冲突的那一块区域，数据很集中，但是其它位置又是空着的，那有没有什么办法，让这些数据稍微分散一点点呢？不要那么集中，于是有人提出了二次探测方法

2.二次探测

线性探测的缺陷是产生冲突的数据堆积在一块，这与其找下一个空位置有关系，因为找空位置的方式就是挨着往后逐个去找，因此二次探测为了避免该问题，找下一个空位置的方法为：Hash(key) = key % n + i2 ( i = 1,2,3… )，通过哈希函数 Hash(key) 计算出元素的关键码 key 对应的位置再加上 i 的平方，n 是表的大小

二次探测相比线性探测的好处：如果一个位置有很多数据冲突，那么二次探测会让这些数据存储位置会比较分散，不会集中在一起，导致一片一片的冲突

---

6.3 闭散列的实现原理与思考

哈希表就是数组，只不过是按照某种映射关系把元素存放进去的数组