C++ 快排思想 求第k大的数据（3种方法）、第k小的数据（3种方法）

C++ 快排思想 求第k大的数据（3种方法）、第k小的数据（3种方法）

#include<iostream>
using namespace std;

//找出数组中第k大的数 法1 二路快排1
int quicksort_k_big1(int a[], int l, int r, int k)//从大到小排序
{
    if (l >= r) return a[l];
    int v = a[l];//基准

    //i，j左右分块的初始值, 要保证初始化时，俩个子数组都为空，即，数组右端索引<左端索引
    int i = l + 1;//a[l+1...i-1]>v
    int j = r;//a[j+1...r]<v

    while (true){
        while (i <= r && a[i] > v) ++i;//降序
        while (j >= l + 1 && a[j] < v) --j;
        if (i > j) break;
        swap(a[i], a[j]);
        ++i;
        --j;
    }
    swap(a[l], a[j]);

    if (j == k) return a[j];
    if (j < k) return quicksort_k_big1(a, j + 1, r, k);
    else return quicksort_k_big1(a, l, j - 1, k);
}

//找出数组中第k小的数 法1_1 二路快排1
int quicksort_k_small1_1(int a[], int l, int r, int k)//从大到小排序
{
    if (l >= r) return a[l];
    int v = a[l];//基准

    //i，j左右分块的初始值, 要保证初始化时，俩个子数组都为空，即，数组右端索引<左端索引
    int i = l + 1;//a[l+1...i-1]>v
    int j = r;//a[j+1...r]<v

    while (true){
        while (i <= r && a[i] > v) ++i;//降序
        while (j >= l + 1 && a[j] < v) --j;
        if (i > j) break;//循环结束标志
        swap(a[i], a[j]);
        ++i;
        --j;
    }
    swap(a[l], a[j]);

    int th = r - k;//设定好 降序时 第k小的数 对应 的是 正序时的 第th大的数

    if (j == th) return a[j];
    if (j < th) return quicksort_k_small1_1(a, j + 1, r, k);
    else return quicksort_k_small1_1(a, l, j - 1, k);
}

//找出数组中第k小的数 法1 二路快排1
int quicksort_k_small1(int a[], int l, int r, int k)//从小到大排序
{
    if (l >= r) return a[l];
    int v = a[l];//基准

    //i，j左右分块的初始值 左:a[l+1...i-1]>v 右:a[j+1...r]<v
    int i = l + 1, j = r;

    while (true){
        while (i <= r  && a[i] < v) ++i;
        while (j >= l + 1 && a[j] > v) --j;

        if (i > j) break;//退出while循环

        swap(a[i], a[j]);
        ++i;
        --j;
    }
    swap(a[l], a[j]);

    if (j == k) return a[j];
    if (j < k) return quicksort_k_small1(a, j + 1, r, k);
    else return quicksort_k_small1(a, l, j - 1, k);
}

//找出数组中第k大的数 法1_1 二路快排1
int quicksort_k_big1_1(int a[], int l, int r, int k)//从小到大排序
{
    if (l >= r) return a[l];
    int v = a[l];//基准

    //i，j左右分块的初始值 左:a[l+1...i-1]>v 右:a[j+1...r]<v
    int i = l + 1, j = r;

    while (true){
        while (i <= r  && a[i] < v) ++i;//升序
        while (j >= l + 1 && a[j] > v) --j;

        if (i > j) break;//退出while循环

        swap(a[i], a[j]);
        ++i;
        --j;
    }
    swap(a[l], a[j]);

    int th = r - k;//设定好 升序时 第k大的数 对应 的是 正序时的 第th小的数

    if (j == th) return a[j];//因为基准元素的索引j是正序的，所以，与转换成正序的第th小的数相比较，会更好一些。
    if (j < th) return quicksort_k_big1_1(a, j + 1, r, k);
    else return quicksort_k_big1_1(a, l, j - 1, k);
}

//找出数组中第k大的数 法2 二路快排2
int quicksort_k_big2(int a[], int l, int r, int k)
{
    if (l >= r) return a[l];
    int v = a[l];

    //i，j左右分块的初始值 左:a[l...i-1]>=v 右:a[j...r]<=v
    int i = l, j = r;
    while (i < j)
    {
        while (i < j && a[j] <= v) --j;
        if (i < j) a[i++] = a[j];
        while (i < j && a[i] >= v) ++i;
        if (i < j) a[j--] = a[i];
    }
    a[i] = v;
    if (i == k) return a[i];
    if (i < k) return quicksort_k_big2(a, i + 1, r, k);
    else return quicksort_k_big2(a, l, i - 1, k);
}

//找出数组中第k小的数 法2 二路快排2
int quicksort_k_small2(int a[], int l, int r, int k)//从小到大排序
{
    if (l >= r) return a[l];
    int v = a[l];

    //i，j左右分块的初始值 左:a[l...i-1]<=v 右:a[j...r]>=v
    int i = l, j = r;

    while (i < j)
    {
        while (i < j && a[j] >= v) --j;
        if (i < j) a[i++] = a[j];
        while (i < j && a[i] <= v) ++i;
        if (i < j) a[j--] = a[i];
    }
    a[i] = v;

    if (i == k) return a[i];
    if (i < k) return quicksort_k_small2(a, i + 1, r, k);
    else return quicksort_k_small2(a, l, i - 1, k);
}

int main()
{
    int a[] = { 100, 8, 4, 6, 5, 98, 0, 7, 100, 4, 8, 0, 8, 2, 1, 9, 3, 6 };
    int n = sizeof(a) / sizeof(a[0]);

    //测试 二路快排 法1 找出数组中第k大的数 
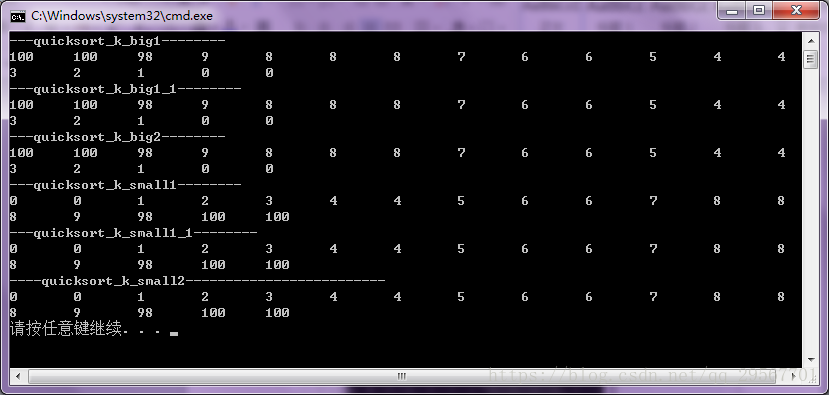
    cout << "---quicksort_k_big1--------" << endl;
    for (int k = 1; k <= n; ++k)//测试从第1-n的所有数据
        cout << quicksort_k_big1(a, 0, n - 1, k - 1) << "\t";
    cout << endl;

    //测试 二路快排 法3 找出数组中第k大的数 
    cout << "---quicksort_k_big1_1--------" << endl;
    for (int k = 1; k <= n; ++k)//测试从第1-n的所有数据
        cout << quicksort_k_big1_1(a, 0, n - 1, k - 1) << "\t";
    cout << endl;

    //测试 二路快排 法2 找出数组中第k大的数 
    cout << "---quicksort_k_big2--------" << endl;
    for (int k = 1; k <= n; ++k)//测试从第1-n的所有数据
        cout << quicksort_k_big2(a, 0, n - 1, k - 1) << "\t";
    cout << endl;

    //测试 找出数组中第k小的数 法1
    cout << "---quicksort_k_small1--------" << endl;
    for (int k = 1; k <= n; ++k)//测试从第1-n的所有数据
        cout << quicksort_k_small1(a, 0, n - 1, k - 1) << "\t";
    cout << endl;

    //测试 找出数组中第k小的数 法1_1
    cout << "---quicksort_k_small1_1--------" << endl;
    for (int k = 1; k <= n; ++k)//测试从第1-n的所有数据
        cout << quicksort_k_small1_1(a, 0, n - 1, k - 1) << "\t";
    cout << endl;

    //测试 找出数组中第k小的数 法2
    cout << "----quicksort_k_small2-------------------------" << endl;
    for (int k = 1; k <= n; ++k)//测试从第1-n的所有数据
        cout << quicksort_k_small2(a, 0, n - 1, k - 1) << "\t";
    cout << endl;

    return 0;
}