克鲁斯卡尔算法JavaScript版

求最小生成树的两种算法：普利姆算法（加点法）& 克鲁斯卡尔算法（加边法）

克鲁斯卡尔算法（加边法）

逻辑：
1)选择最短的边进行连接
2)边的两端至少有一个是未连接的节点，或者边两端的节点不在同一个部落中
3)将符合连接条件的最短边进行连接，重复1,2步骤
4)直到所有的节点都被连接，且都在一个部落

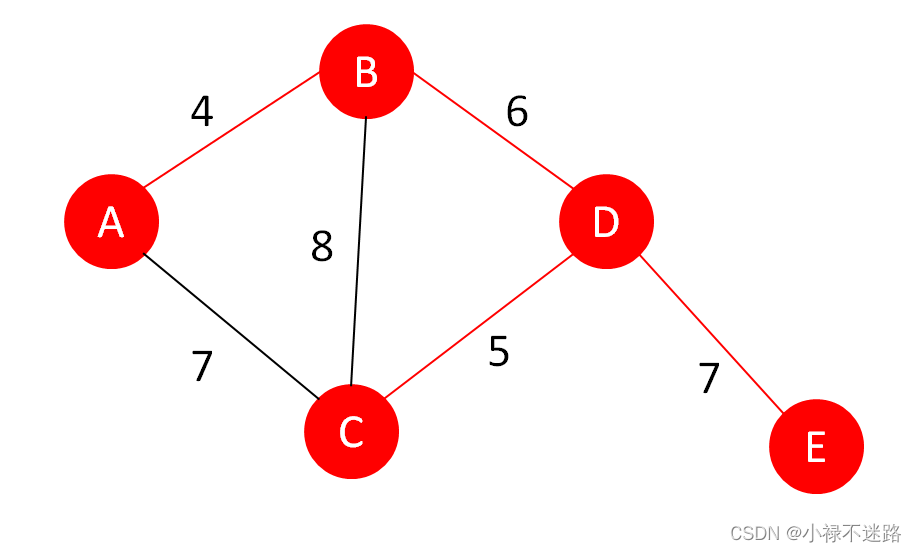
有A、B、C、D、E 5个村庄，它们之间的距离如图示：

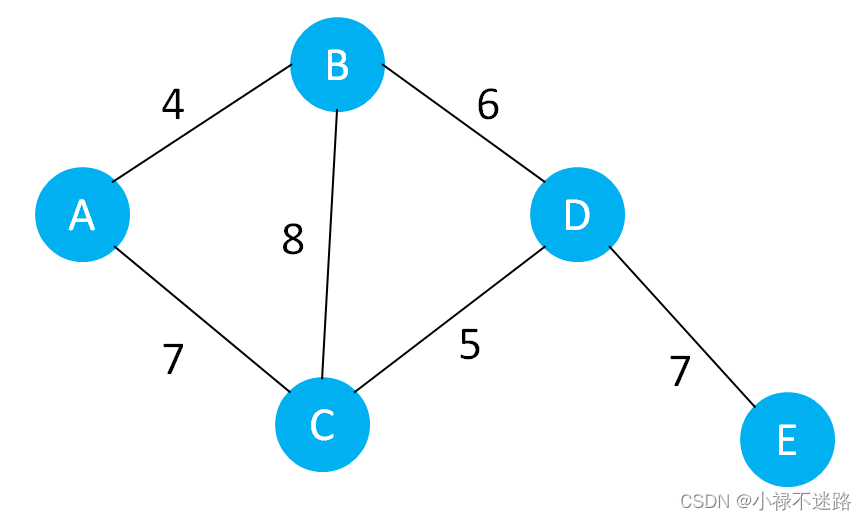
连接过程如下：
1.找到符合连接条件的最短边为A、B节点间的边，进行连接形成第一个部落。

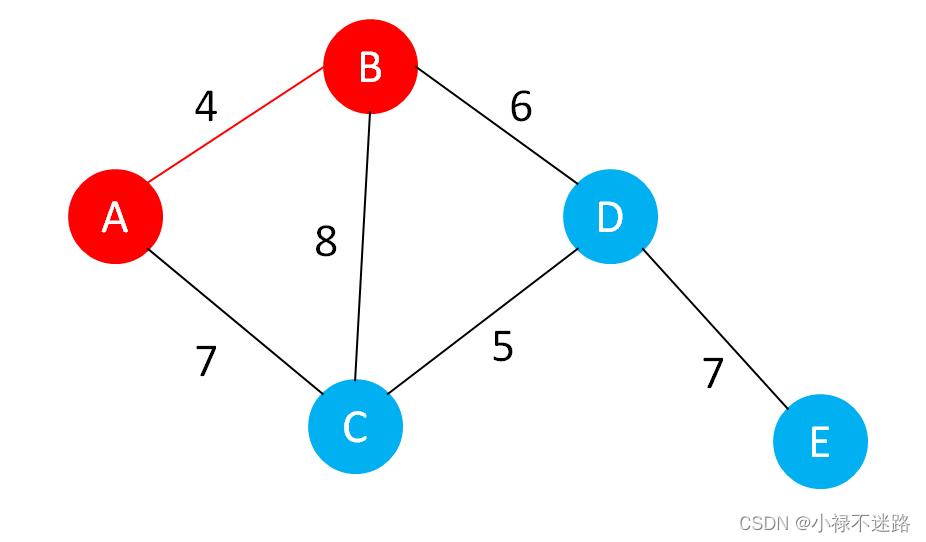
2.找到符合条件的最短的边为C、D节点之间的边，进行连接形成第二个部落。

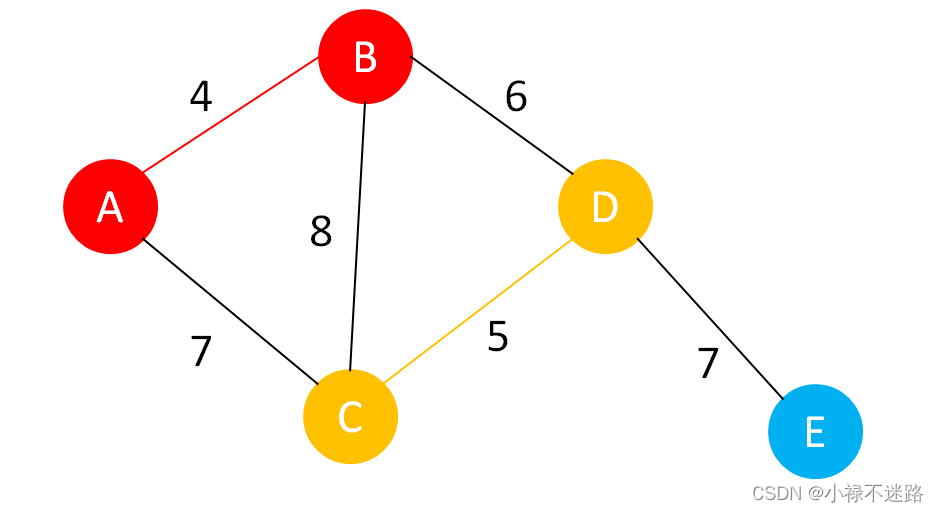
3.找到符合条件的最短边为B、D节点之间的边，进行连接，将两个部落连接成为一个部落。

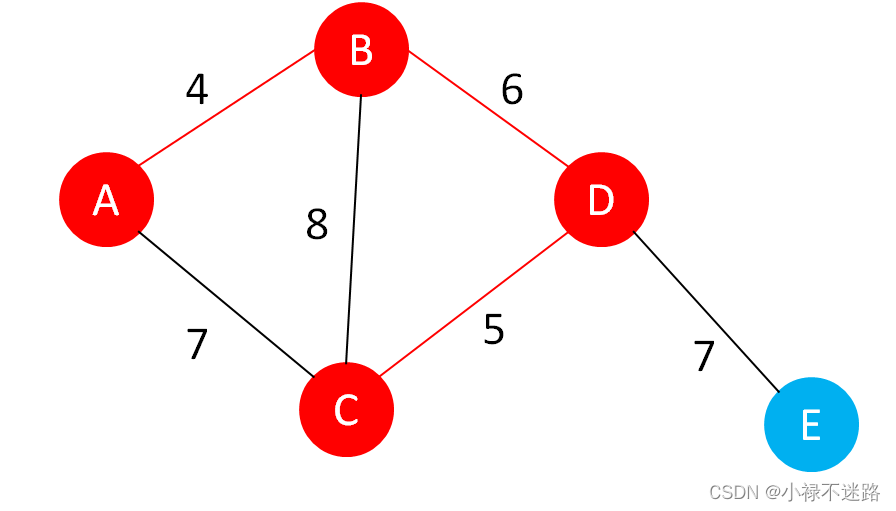
4.找到符合条件的边为D、E节点之间的边，进行连接，将E节点连入部落。所有节点全部连接，且只有一个部落，连接完成。

var MAX_DISTANCE = 1000000;
var pointSet = ["A", "B", "C", "D", "E"];
var distance = [
  [0, 4, 7, MAX_DISTANCE, MAX_DISTANCE],
  [4, 0, 8, 6, MAX_DISTANCE],
  [7, 8, 0, 5, MAX_DISTANCE],
  [MAX_DISTANCE, 6, 5, 0, 7],
  [MAX_DISTANCE, MAX_DISTANCE, MAX_DISTANCE, 7, 0],
];

class Node {
  constructor(val) {
    this.val = val;
    this.neighbor = [];
  }
}

let pointList = new Array(pointSet.length)
  .fill("0")
  .map((item, index) => new Node(pointSet[index]));

function Kruskal(pointList, distanceList) {
  //这是一个二维数组，表示部落及部落中的节点
  let resultList = [];
  while (true) {
    //找出符合连接条件的最短的边，和边的两端节点
    let minDisEdge = MAX_DISTANCE;
    let node1 = null;
    let node2 = null;
    for (let i = 0; i < distanceList.length; i++) {
      for (let j = 0; j < distanceList[i].length; j++) {
        //判断两个节点能否满足连接条件
        let flag = canLink(pointList[i], pointList[j], resultList);
        if (i != j && distanceList[i][j] < minDisEdge && flag) {
          minDisEdge = distanceList[i][j];
          node1 = pointList[i];
          node2 = pointList[j];
        }
      }
    }
    //连接节点
    linkNode(node1, node2, resultList);
    if (
      resultList &&
      resultList.length === 1 &&
      resultList[0].length === pointList.length
    ) {
      break;
    }
  }
}

//判断能否连接该边
//两个点不存在resultList中，则两个点都是新连接的节点，连接形成一个新的部落，加入到resultList中
//有一个点存在于resultList的一个部落中，另一个点不存在于resultList中，可以连接，扩展部落
//两个点都在resultList中，但是属于不同的部落，可以连接的，形成一个部落
//两个点都在resultList中，它们属于相同的部落，不可以连接

/***
 * 根据两个节点和已连接的部落，判断能否连接两个节点
 * @param {Node} node1:最短边的一个节点
 * @param {Node} node1:最短边的另一个节点
 * @param {*} resultList：已经连接的部落及节点
 * @return boolean
 */
function canLink(node1, node2, resultList) {
  if (!node1 || !node2) {
    return false;
  }
  let tribe1 = null; //node1所在的部落
  let tribe2 = null; //node2所在的部落
  for (let i = 0; i < resultList.length; i++) {
    if (resultList[i].indexOf(node1) > -1) {
      tribe1 = resultList[i];
    }
    if (resultList[i].indexOf(node2) > -1) {
      tribe2 = resultList[i];
    }
  }
  //两个点不存在resultList中，则两个点都是新连接的节点，连接形成一个新的部落，加入到resultList中
  if (!tribe1 && !tribe2) {
    return true;
  } else if ((tribe1 && !tribe2) || (!tribe1 && tribe2)) {
    return true;
  } else if (tribe1 !== tribe2) {
    return true;
  }
  //两个节点在同一个部落的不满足连接条件
  return false;
}

/**
 *
 * @param {*} node1 满足连接条件的最短边的一个节点
 * @param {*} node2 满足连接条件的最短边最短边的另一个节点
 * @param {*} resultList已连接的部落及部落节点
 */
function linkNode(node1, node2, resultList) {
  if (!node1 || !node2) {
    return false;
  }
  if (!node1 || !node2) {
    return false;
  }
  let tribe1 = null; //node1所在的部落
  let tribe2 = null; //node2所在的部落
  for (let i = 0; i < resultList.length; i++) {
    if (resultList[i].indexOf(node1) > -1) {
      tribe1 = resultList[i];
    }
    if (resultList[i].indexOf(node2) > -1) {
      tribe2 = resultList[i];
    }
  }
  //两个点不存在resultList中，则两个点都是新连接的节点，连接形成一个新的部落，加入到resultList中
  if (!tribe1 && !tribe2) {
    node1.neighbor.push(node2);
    node2.neighbor.push(node1);
    resultList.push([node1, node2]);
  } else if (tribe1 && !tribe2) {
    node2.neighbor.push(node1);
    tribe1.push(node2);

    let index = tribe1.indexOf(node1); //找出node1在tribe1（部落1）的位置
    tribe1[index].neighbor.push(node2);
  } else if (!tribe1 && tribe2) {
    node1.neighbor.push(node2);
    tribe2.push(node1);

    let index = tribe2.indexOf(node2); //找出node2在tribe2（部落2）的位置
    tribe2[index].neighbor.push(node1);
  } else if (tribe1 !== tribe2) {
    //两个节点都存在于resultList中的部落
    //两个节点不在相同的部落，则连接两个部落，形成一个部落
    let index1 = tribe1.indexOf(node1); //node1在tribe1的位置
    let index2 = tribe2.indexOf(node2); //node2在tribe2的位置
    tribe1[index1].neighbor.push(tribe2[index2]);
    tribe2[index2].neighbor.push(tribe1[index1]);
    tribe1.push(...tribe2); //将tribe2连接到tribe1
    //找到tribe2在resultList中的位置，并删除
    let index = resultList.indexOf(tribe2);
    resultList.splice(index, 1);
  }
  //两个节点在同一个部落的不满足连接条件，不连接
}

Kruskal(pointList, distance);
console.log(pointList);