LeetCode刷题之旅（中等 -2）：997. 找到小镇的法官

最新推荐文章于 2021-04-06 00:23:46 发布

原创最新推荐文章于 2021-04-06 00:23:46 发布 · 512 阅读

CC 4.0 BY-SA版权

本文深入解析图数据结构，包括无向图、有向图、完全图、DAG图等概念，探讨图的连通性、权重及特殊边类型。通过实例讲解图的邻接顶点、顶点的度，以及在算法设计中的应用，如深度优先搜索和广度优先搜索。同时，提供了三种求解法官问题的方法，包括统计出入度、使用数组记录出入度和简化统计出入度的实现。

2019年9月13日

《数据结构与算法》的积累进度较慢，抓住中秋佳节，完善自己。

10.简单图 ( Simple Graph)

题目：

图的数据结构：

图的概念

图（Graph）是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G（V,E），其中，G表示一个图，V是图中G中顶点的集合，vertex；E是图G中边的集合，edge。

图有两种：无向图和有向图。

1.无向图

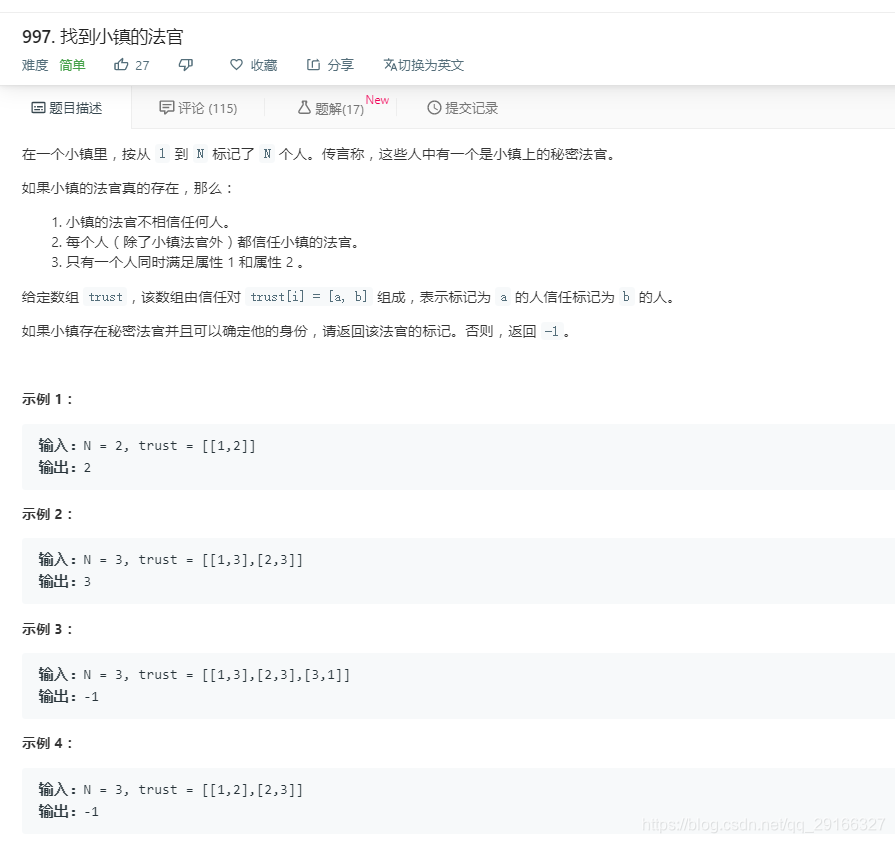
无向图：若两个顶点没有方向，则称这条边为无向边。如果图中任意两个顶点之间的边都是无向边，则称该图为无向图（如下图所示）。在无向图中，若任意两个顶点之间都存在边，则称为无向完全图。

典型的无向图，如图二所示。由于无向图中的边没有方向性，这样我们在表示边的时候对两个顶点的顺序没有要求。例如顶点VI和顶点V5之间的边，可以表示为(V2， V6),也可以表示为(V6，V2)。

图二无向图

对于图二无向图，对应的顶点集合和边集合如下：

V（G）= {V1，V2，V3，V4，V5，V6}

E（G）= {（V1,V2），（V1，V3），（V2，V6），（V2，V5），（V2，V4），（V4，V3），（V3，V5），（V5，V6）}

2.有向图

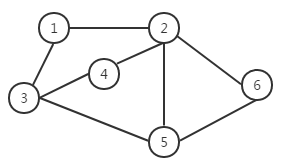
一个图结构中，边是有方向性的，那么这种图就称为有向图，如图三所示。由于图的边有方向性，我们在表示边的时候对两个顶点的顺序就有要求。我们采用尖括号表示有向边，例如<V2，V6>表示从顶点V2到顶点V6，而<V6，V2>表示顶点V6到顶点V2。

图三有向图

对于图三有向图，对应的顶点集合和边集合如下：

V（G）= {V1，V2，V3，V4，V5，V6}

E（G）= {<V2，V1>，<V3，V1>，<V4，V3>，<V4，V2>，<V3，V5>，<V5，V3>，<V2，V5>，<V6，V5>，<V2，V6>，<V6，V2>}

注意：

无向图也可以理解成一个特殊的有向图，就是边互相指向对方节点，A指向B，B又指向A。

3.顶点的度

连接顶点的边的数量称为该顶点的度。顶点的度在有向图和无向图中具有不同的表示。对于无向图，一个顶点V的度比较简单，其是连接该顶点的边的数量，记为D(V)。例如，图二所示的无向图中，顶点V5的度为3。而V6的度为2。

对于有向图要稍复杂些，根据连接顶点V的边的方向性，一个顶点的度有入度和出度之分。

入度是以该顶点为端点的入边数量，记为ID(V)。
出度是以该顶点为端点的出边数量，记为OD(V)。

这样，有向图中，一个顶点V的总度便是入度和出度之和，即D(V) = ID(V) + OD(V)。例如，图三所示的有向图中，顶点V5的入度为3,出度为1，因此，顶点V5的总度为4。

4.邻接顶点

邻接顶点是指图结构中一条边的两个顶点。邻接顶点在有向图和无向图中具有不同的表示。对于无向图，邻接顶点比较简单。例如，在图二所示的无向图中，顶点V2和顶点V6互为邻接顶点，顶点V2和顶点V5互为邻接顶点等。

对于有向图要稍复杂些，根据连接顶点V的边的方向性，两个顶点分别称为起始顶点(起点或始点)和结束顶点(终点)。有向图的邻接顶点分为两类：

入边邻接顶点：连接该顶点的边中的起始顶点。例如，对于组成<V2，V6>这条边的两个顶点，V2是V6的入边邻接顶点。
出边邻接顶点：连接该顶点的边中的结束顶点。例如，对于组成<V2，V6>这条边的两个顶点，V6是V2的出边邻接顶点。

5.无向完全图

如果在一个无向图中，每两个顶点之间都存在条边，那么这种图结构称为无向完全图。典型的无向完全图，如图四所示。

图四无向完全图

理论上可以证明，对于一个包含M个顶点的无向完全图，其总边数为M(M-1)/2。比如图四总边数就是5（5-1）/ 2 = 10。

6.有向完全图

如果在一个有向图中，每两个顶点之间都存在方向相反的两条边，那么这种图结构称为有向完全图。典型的有向完全图，如图五所示。

图五有向完全图

理论上可以证明，对于一个包含N的顶点的有向完全图，其总的边数为N(N-1)。这是无向完全图的两倍，这个也很好理解，因为每两个顶点之间需要两条边。

7.有向无环图（DAG图）

　　　　如果一个有向图无法从某个顶点出发经过若干条边回到该点，则这个图是一个有向无环图。

　　　　有向无环图可以利用在区块链技术中。

　　8.无权图和有权图

这里的权可以理解成一个数值，就是说节点与节点之间这个边是否有一个数值与它对应，对于无权图来说这个边不需要具体的值。对于有权图节点与节点之间的关系可能需要某个值来表示，比如这个数值能代表两个顶点间的距离，或者从一个顶点到另一个顶点的时间，所以这时候这个边的值就是代表着两个节点之间的关系，这种图被称为有权图；

9.图的连通性

图的每个节点不一定每个节点都会被边连接起来，所以这就涉及到图的连通性，如下图：

可以发现上面这个图不是完全连通的。

10.简单图 ( Simple Graph)

对于节点与节点之间存在两种边，这两种边相对比较特殊

　　1.自环边（self-loop）：节点自身的边，自己指向自己。

　　2.平行边（parallel-edges）：两个节点之间存在多个边相连接。

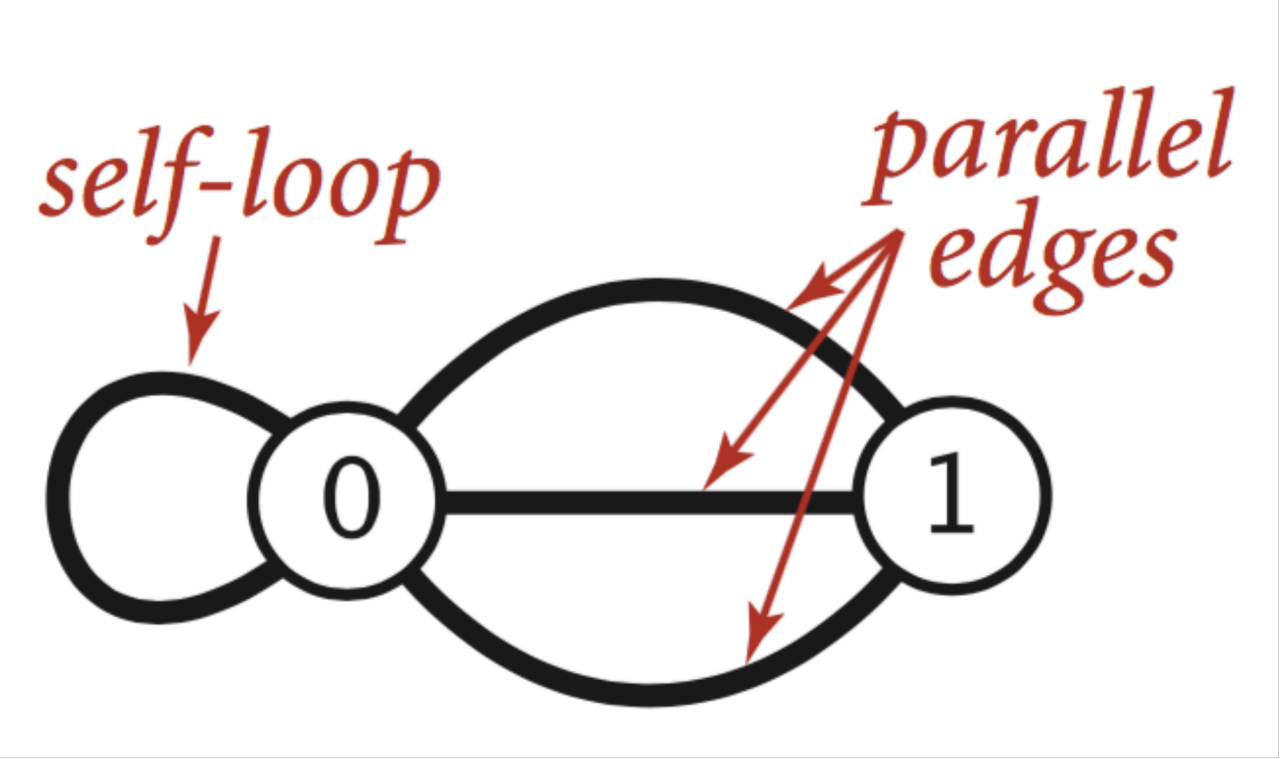
这两种边都是有意义的，比如从A城市到B城市可能不仅仅有一条路，比如有三条路，这样平行边就可以用到这种情况。不过这两种边在算法设计上会加大实现的难度。而简单图就是不考虑这两种边。

实现图的深度优先搜索、广度优先搜索

解决方法1：统计出入度


public class FindJudgeSolution {

	public static void main(String[] args){
		int N = 3;
		int[][] trust = {{1,3},{2,3}};

		int result = findJudge(N, trust);
		System.out.println("result = "+ result);

	}

	public static int findJudge(int N, int[][] trust) {
		int[] cnt = new int[N+1];//统计出入度
		for (int[] index : trust) {
			cnt[index[0]]--;//出度--
			cnt[index[1]]++;//入度++
		}
		for ( int i = 1; i <= N; i++ ) {
			if ( cnt[i] == N-1 ) return i;
		}
		return -1;
	}
}

性能结果：

解题思路：

法官节点：入度为N-1，出度为0接着就是遍历图（二维数据）

解决方法2：

class Solution {
    public int findJudge(int N, int[][] trust) {
        int inDegree[]  = new int[1001];       // 定义两个数组分别存储每一个节点的入度和出度
		int	outDegree[] = new int[1001];                     
    	int peopleMark;                            // 记录人的编号 
    	for(int i = 0; i < trust.length; i++) {
    		peopleMark = trust[i][0];
			outDegree[peopleMark]++;               // 人的出度加1 
			
			peopleMark = trust[i][1];
			inDegree[peopleMark]++;                // 人的入度加 1
    	}
    	for(int i = 1; i <= N; i++){               // 判断一个人的出度和入度来判断是否是法官 
			if(inDegree[i] == (N - 1) && outDegree[i] == 0)
				return i; 
		}   	           
		return -1;  
    }
}

作者：lu-zhao
链接：https://leetcode-cn.com/problems/find-the-town-judge/solution/xiao-bai-ben-ban-fa-by-lu-zhao/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

解决方法3：

class Solution {
    public int findJudge(int N, int[][] trust) {
        int [][] b = new int[N][2];
        for (int i = 0; i < N; i++) {
            b[i][0] = 0;
            b[i][1] = 0;
        }
        for (int i = 0; i < trust.length; i++) {
            b[trust[i][0] - 1][0]++;
            b[trust[i][1] - 1][1]++;
        }
        int g = -1;
        for (int i = 0; i < N; i++) {
            if (b[i][0] == 0 && b[i][1] == N -1) {
                if (g != -1) {
                    return -1;
                }
                g = i + 1;
            }
        }
        return g;
    }
}

作者：lan-de-xiao-mai
链接：https://leetcode-cn.com/problems/find-the-town-judge/solution/javashi-xian-tong-ji-chu-ru-du-by-lan-de-xiao-mai/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

参考：https://www.cnblogs.com/songgj/p/9107797.html