二叉树及其操作：顺序储存、遍历与哈夫曼树实现-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_28414091/article/details/129634308

二叉树顺序储存

顺序完全二叉树

#include<iostream>
using namespace std;

int main()
{
    int n;
    cin >> n;
    
    char * tree = new char[n + 1];
    tree[0] = '0';
    for (int i = 1; i <= n; i++)
    {
        cin >> tree[i];
    }
        
    char value;
    cin >> value;
    
    for (int i = 1; i <= n; i++)
    {
        if (value - tree[i] == 0)
        {
            cout << tree[i / 2];
        }
    }
        
    return 0;
}

链式树

#include<iostream>
using namespace std;

template<class T>
class tNode
{
public:
    T data;
    tNode *pL, *pR;
};

const int MAXSIZE = 20000;
tNode<char> tree [MAXSIZE];
int N;

int main()
{
    int L, R;
    int id;
    char a;
        
    // 构建二叉树
    cin >> N;
    for (int i = 0; i < N; i++)
    {
        cin >> id >> a >> L >> R;
        tree[id].data = a;
        if (!L)
        {
            tree[id].pL = NULL;
        }
        else
        {
            tree[id].pL = &tree[L];
        }
        if (!R)
        {
            tree[id].pR = NULL;
        }
        else
        {
            tree[id].pR = &tree[R];
        }
    }
    
    tNode<char> *p = &tree[1]; // 搜索
    while(p)
    {
        cout << p->data << " ";
        p = p->pL;
    }
        
    return 0;
}

/*
测试
4
1 a 3 8
8 c 0 0
4 d 0 0
3 b 4 0
*/

二叉树前序遍历、中序遍历、后序遍历

#include<iostream>
#include<queue>
using namespace std;

template<class T>
class tNode
{
public:
    T data;
    tNode *pL, *pR;
};

// 前序遍历
template<class T>
void preOrder(tNode<T> * root)
{
    if (root == NULL)
    {
        return;
    }
    cout << root->data << endl;
    preOrder(root->pL);
    preOrder(root->pR);
}

// 中序遍历
template<class T>
void midOrder(tNode<T> * root)
{
    if (root == NULL)
    {
        return;
    }
    midOrder(root->pL);
    cout << root->data << endl;
    midOrder(root->pR);
}

// 后序遍历
template<class T>
void backOrder(tNode<T> * root)
{
    if (root == NULL)
    {
        return;
    }
    backOrder(root->pL);
    backOrder(root->pR);
    cout << root->data << endl;
}

// 层序遍历
template<class T>
void levelOrder(tNode<T> *t)
{
    queue<tNode<char> *> q;
    q.push(t); 
    while(1)
    {
        if (q.empty())
            break;
        cout << q.front()->data << endl;
        if (q.front()->pL != NULL)
            q.push(q.front()->pL);
        if (q.front()->pR != NULL)
            q.push(q.front()->pR);
        q.pop();
    }
}


const int MAXSIZE = 20000;
tNode<char> tree [MAXSIZE];
int N;

int main()
{
    int L, R;
    int id;
    char a;
        
    // 构建二叉树
    cin >> N;
    for (int i = 0; i < N; i++)
    {
        cin >> id >> a >> L >> R;
        tree[id].data = a;
        if (!L)
        {
            tree[id].pL = NULL;
        }
        else
        {
            tree[id].pL = &tree[L];
        }
        if (!R)
        {
            tree[id].pR = NULL;
        }
        else
        {
            tree[id].pR = &tree[R];
        }
    }
    
        
    cout << "前序遍历" << endl;
    preOrder(tree + 1);
    cout << endl;
    
    cout << "中序遍历" << endl;
    midOrder(tree + 1);
    cout << endl;
    
    cout << "后序遍历" << endl;
    backOrder(tree + 1);
    cout << endl;
    
    cout << "层序遍历" << endl;
    levelOrder(tree + 1);
    cout << endl;
        
    return 0;
}

/*
测试
6
1 A 2 3 
2 B 0 5
3 C 4 0
4 D 0 0
5 E 6 0
6 F 0 0
*/

一般树的构建和前序后序及层序遍历

#include<iostream>
#include<queue>
using namespace std;

const int MAXSIZE = 20000;
const int dMAX = 5;
int N;

// 一般树的节点
template<class T>
class tNode
{
public:
    T data;
    tNode *sons[dMAX];
};

tNode<char> tree [MAXSIZE];

// 一般树的前序遍历
template<class T>
void preOrder(tNode<T> * root)
{
    if (root == NULL)
    {
        return;
    }
    cout << root->data << endl;
    for (int i = 0; i < dMAX; i++)
    {
        if (root->sons[i] != NULL)
        {
            preOrder(root->sons[i]);
        }
    }
}

// 一般树的后序遍历
template<class T>
void backOrder(tNode<T> * root)
{
    if (root == NULL)
    {
        return;
    }
    for (int i = 0; i < dMAX; i++)
    {
        if (root->sons[i] != NULL)
        {
            backOrder(root->sons[i]);
        }
    }
    cout << root->data << endl;
}

// 一般树的层序遍历
queue<tNode<char> *> q;
template<class T>
void levelOrder(tNode<T> * root)
{
    if (root == NULL)
    {
        return;
    }
    q.push(root);
    while(1)
    {
        cout << q.front()->data << endl;
        for (int i = 0; i < dMAX; i++)
        {
            if (q.front()->sons[i] != NULL)
            {
                q.push(q.front()->sons[i]);
            }
        }
        q.pop();
    }
}

int main()
{
    int s[dMAX];
    int id;
    char a;
        
    // 构建一般树
    cin >> N;
    for (int i = 0; i < N; i++)
    {
        cin >> id >> a;
        for (int j = 0; j < dMAX; j++)
        {
            cin >> s[j];
        }
        tree[id].data = a;
        for (int j = 0; j < dMAX; j++)
        {
            if (s[j] != 0)
            {
                tree[id].sons[j] = &tree[s[j]];
            }
        }
    }
        
    
    cout << "前序遍历" << endl;
    preOrder(tree + 1);    
    cout << endl;
    
    cout << "后序遍历" << endl;
    backOrder(tree + 1);
    cout << endl;

    cout << "层序遍历" << endl;
    levelOrder(tree + 1);
    cout << endl;
        
    return 0;
}

/*
测试
6
1 A 2 3 4 0 0
2 B 0 0 0 0 0
3 C 0 0 5 0 6
4 D 0 0 0 0 0
5 E 0 0 0 0 0
6 F 0 0 0 0 0
*/

二叉排序树

#include<iostream>
#include<stack>
using namespace std;
 
template<class T>
class tNode
{
public:
    T data;
    tNode *pL, *pR;
};

// 二叉排序树节点的递归插入
template<class T>
void insertNode(tNode<T> * &root, T x)
{
    if (!root)
    {
        tNode<T> *r = new tNode<T>;
        r->pL = r->pR = NULL;
        r->data = x;
        root = r;
        return;
    }
    if (x < root->data)
    {
        insertNode(root->pL, x);
    }
    else
    {
        insertNode(root->pR, x);
    }
}

// 二叉排序树节点的非递归插入
template<class T>
void insertNode1(tNode<T> * r, T x)
{
    tNode<T> * tmp = new tNode<T>;
    tmp->data = x;
    tmp->pR = tmp->pL = NULL;
    while(r)
    {
        if (x < r->data)
        {
            if (!r->pL)
            {
                r->pL = tmp;
                return;
            }
            else
            {
                r = r->pL;
            }
        }
        else
        {
            if (!r->pR)
            {
                r->pR = tmp;
                return;
            }
            else
            {
                r = r->pR;
            }
        }
    }
}

// 找到二叉排序树某一节点的前驱，用于删除有两个儿子的节点
template<class T>
tNode<T> * findpre(tNode<T> * cur, tNode<T> * &fa)
{
    fa = cur;
    tNode<T> * pre = cur->pL;
    while(pre->pR)
    {
        fa = pre;
        pre = pre->pR;
    }
    return pre;
}

// 二叉排序树节点的删除
template<class T>
void deleteNode(tNode<T> *root, T x)
{
    tNode<T> * fa = NULL;
    tNode<T> * cur = root;
    if (root)
    {
        // 找到待删除节点
        while(cur && cur->data != x)
        {
            if (x < cur->data)
            {
                fa = cur;
                cur = cur->pL;
            }
            else
            {
                fa = cur;
                cur = cur->pR;
            }
        }
        if (cur)
        {
            // 若待删除节点没有左右儿子
            if (!cur->pL && !cur->pR)
            {
                // 判断待删除节点是父节点的左儿子还是右儿子
                bool flagL = 1;
                if (fa->pL != cur)
                {
                    flagL = 0;
                }
                if (flagL == 1)
                {
                    delete cur;
                    fa->pL = NULL;
                }
                else
                {
                    delete cur;
                    fa->pR = NULL;
                }
            }
            // 若待删除节点有左儿子且有右儿子
            else if (cur->pL && cur->pR)
            {
                tNode<T> * tmp = NULL;
                tNode<T> * place = findpre(cur, tmp);
                cur->data = place->data;
                bool flagL = 1;
                if (tmp->pL != place)
                {
                    flagL = 0;
                }
                if (flagL == 1)
                {
                    tmp->pL = place->pL;
                    delete place;
                }
                else
                {
                    tmp->pR = place->pL;
                    delete place;
                }
                
            }
            // 若待删除节点仅有左儿子或右儿子
            else
            {
                // 判断待删除节点是父节点的左儿子还是右儿子
                bool flagL = 1;
                if (fa->pL != cur)
                {
                    flagL = 0;
                }
                if (flagL == 1)
                {
                    if (cur->pL)
                    {
                        fa->pL = cur->pL;
                    }
                    else
                    {
                        fa->pL = cur->pR;
                    }
                }
                else
                {
                    if (cur->pL)
                    {
                        fa->pR = cur->pL;
                    }
                    else
                    {
                        fa->pR = cur->pR;
                    }
                }
            }
        }
    }
}

//二叉排序树的查找
template<class T>
tNode<T> * findNode(tNode<T> * root, T x)
{
    tNode<T> * cur = root;
    while(cur && cur->data != x)
    {
        if (x < cur->data)
        {
            cur = cur->pL;
        }
        else
        {
            cur = cur->pR;
        }
    }
    return cur;
}

int main()
{
    int n;
    cin >> n;
    int a[10000];
    for (int i = 0; i < n; i++)
    {
        cin >> a[i];
    }
    
    tNode<int> *root = NULL;
    
    for (int i = 0; i <  n; i++)
    {
        insertNode(root, a[i]);
    }
    
    preOrder(root); // 二叉树的前序遍历，代码在前面给出，中序遍历同
    cout << endl;
    midOrder(root);
    cout << endl;
    
    deleteNode(root, 8);
    
    preOrder(root);
    cout << endl;
    midOrder(root);
    return 0;
}

/*
测试
10
8 2 10 1 5 14 4 7 13 6
*/

测试用例

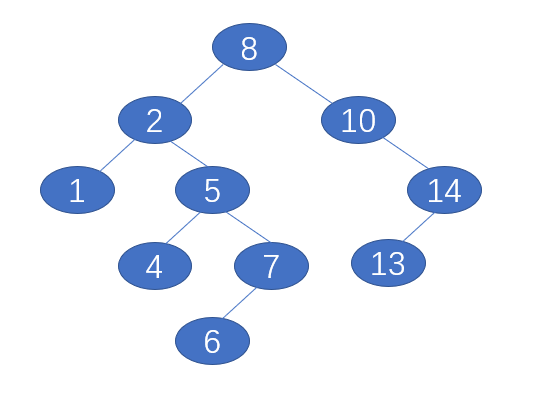
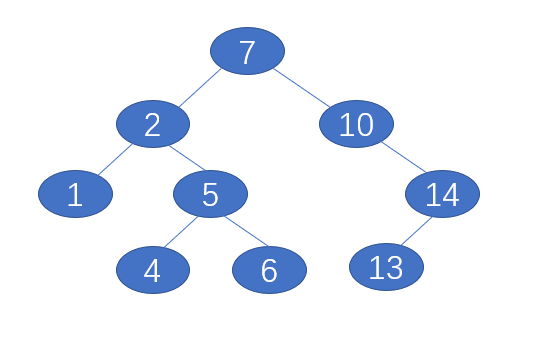
删除节点8后

树的递归释放

template<class T>
void freeTree(tNode<T> * root)
{
    if (root)
    {
        freeTree(root->pL);
        freeTree(root->pR);
        delete root;
    }
}

哈夫曼树

#include <bits/stdc++.h>
using namespace std;

#define INF_WEIGHT 1000000

struct tNode
{
    int weight;
    int father;
    int left;
    int right;    
};

tNode * hfmCreate(int * w, int n)
{
    tNode * ht = new tNode[2 * n];
    int k, i;
    
    ht[0].weight = n;
    // n个权值节点ht[1]~ht[n]初始化为叶节点
    for (k = 1; k <= n; k++)
    {
        ht[k].weight = w[k - 1];
        ht[k].father = -1;
        ht[k].left = -1;
        ht[k].right = -1;
    }
    // 生成n -1个非叶节点ht[n + 1]~ht[2 * n - 1]
    for (k = n + 1; k <= 2 * n - 1; k++)
    {
        // 在ht[1]~ht[k - 1]中找权值最小的两棵树first,second
        ht[k].weight = INF_WEIGHT;
        int first = k;
        int second = k;
        
        for (i = 1; i < k; i++)
        {
            if (ht[i].father < 0 && ht[i].weight < ht[first].weight)
            // 找到更小的，那么第二小的改为原来最小的
            {
                second = first;
                first = i;
            }
            else 
            {
                if (ht[i].father < 0 && ht[i].weight < ht[second].weight)
                {
                    second = i;
                }
            }
        }
        // 创建两个最小节点的父节点ht[k]，修改它们的父节点指针
        ht[k].weight = ht[first].weight + ht[second].weight;
        ht[k].left = first;
        ht[k].right = second;
        ht[k].father = -1;
        ht[first].father = k;
        ht[second].father = k;
    }
    return ht;
}

int main()
{
    int n;
    int * w;
    cin >> n;
    for (int i = 0; i < n; i++)
    {
        cin >> w[i];
    }
    
    cout << hfmCreate(w, n)[2 * n - 1].weight << endl;
    
    return 0;
}

/*
测试
6
3 5 8 9 10 11
*/

C++：树