大话数据第四天

栈的应用：四则运算表达式求值

1. 后缀表达式
2. 中缀表达式转后缀表达式

队列

定义：队列是允许在一端进行插入操作，而在另一端进行删除操作的线性表。允许插入的叫队尾，允许删除的一端称为对头

 

循环队列

    假设一个队列有n个元素，则顺序存储的队列序建立一个大于n的数组，并把队列的所有元素存储在数组的前n个单元中，数组下标为0的一端即是对头。当队列要出队时，所有的元素就需要向前移动，但是如果不去限制队列的元素必须存储在前n个单元这一条件，出队的性能就增加。

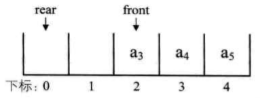
入队       (front指向对头元素，rear指向队尾的下一个位置)  插入a1、a2、a3、a4

出队       a1、a2出队  ，front指针向后移    当如果在插入a5时，rear向后移，再插入就溢出

则就出现循环队列

将上面的rear指针指向数组开头的位置

而当front和rear相等时，就要判断队列是否为空，还是为满

• 方法一：设置一个标志变量flag，当front==rear，且flag=0时队尾为空，flag=1时为队列满

    

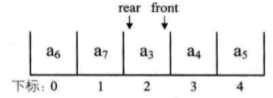
• 方法二：保留一个元素空间，当队列满时，数组中还有一个空闲单元    判断条件：(rear+1)%QueueSize==front，例如，下图，

       左图(front=0，rear=4，QueueSize=5，公式(4+1)%5=0--满队列)   

       右图(front=2，rear=1，QueueSize=5，公式(1+1)%5=2--满队列)

       通用的队列长度计算公式：（rear+QueueSize-front）%QueueSize

    

 

五、 串

子串的定位操作通常称为串的模式匹配

朴素的模式匹配算法

KMP模式匹配算法

    有主串S，目标字符串T，在串S中匹配T，当从一个位置开始匹配时：

    

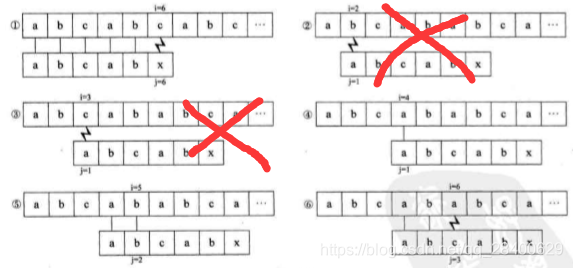
     如下图，T="abcdex"，当中没有任何重复的字符，所以j就由6变为1。

   

    下图，T="abcabx"，前缀的"ab"与最后"x"之前的后缀"ab"时相等的，j由6变为3

   

    即j值的变化取决与当前字符串之前的串的前缀与后缀的相似度   

    把T串各个位置j值的变化定义为一个数组next，那么next的长度就是T串的长度。

    

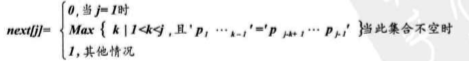
    例：(该例子来源于大话数据结构)

  

如果前后缀一个字符相等，k值是2，两个字符相等，k值是3，n个字符相等，k等于n+1

上述的next()出现问题

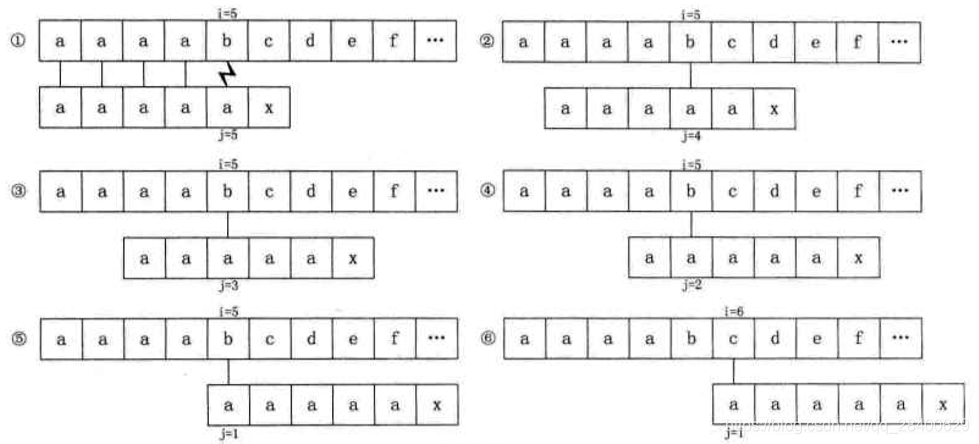
上述中2、3、4、5是可以省掉的，T串中前n个字符相等

从而有nextval()计算方法

前缀和后缀详解(PMT，Partial Match Table-部分匹配表)   字符串本身不是他自己的前缀和后缀

PMT表：

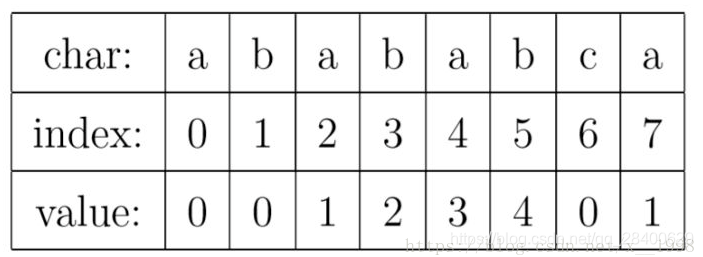
Harry的前缀：{'H','Ha','Har','Harr'}  

Potter的后缀：{'otter','tter','ter','er','r'}

PMT的值是字符串所有前缀组成的集合与后缀集合的交集中最长元素的的长度

所以"aba"，前缀{"a","ab"}，后缀{"ba","a"}，交集为{"a"}，长度为1

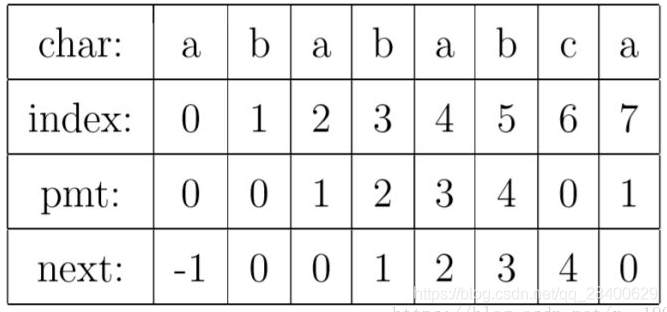
将第0位的值设为-1，只是为了编程的方便  在第j位失配，那么影响j指针回溯的位置其实是第j-1位的pmt值