常见算法之排序算法总结（3）-优快云博客

本文详细介绍了五种常见的排序算法：选择排序、冒泡排序、插入排序、归并排序和快速排序。每种算法的实现原理、时间复杂度、空间复杂度以及稳定性进行了分析。其中，归并排序和快速排序在平均情况下具有较高的效率，而插入排序在部分有序数据中表现优秀。此外，还提到了堆排序的基本思想和流程，以及各种排序算法在实际应用中的优缺点。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

选择排序

每次选取出最小值或者最大值放在数组前面或者后面

外面循环：表示有总数N个数，要操作N次。

里面循环：是data[i]和i后面的每个数比较，小于data[i]交换位置，然后data[i]和剩下的数比较，这样下来data[i]就是i到length上的最小值。

    public static void choseSort(int[] data) {
        int length = data.length;
        for (int i = 0; i < length; i++) {
            for (int j = i + 1; j < length; j++) {
                if (data[j] < data[i]) {
                    swap(data, i, j);
                }
            }
        }
    }

冒泡排序

相邻两个数比较，大于或者小于就交换。

外面循环：表示有总数N个数，要操作N次。

里面循环：前一个数和后一个数比较，大于后面一个数就交换，然后这个数和后面的数又比较直到结束。这样一次选取出i个有序的大的数排在数组后面，循环length - i次就能比较完所有数。

    public static void bubbleSort(int[] data) {
        int length = data.length;
        for (int i = 0; i < length; i++) {
            for (int j = 0; j + 1 < length - i; j++) {
                if (data[j] > data[j + 1]) {
                    swap(data, j, j + 1);
                }
            }
        }
    }

插入排序

保证前面的i-1个数有序，然后在前面有序数列中插入新的数。

外面循环：表示有总数N个数，要操作N次。

里面循环：j = i - 1，j + 1 = i。i-1位置是有序的，插入新的数data[i],然后和前面的数比较，小于前面的数就交换，这样新的数列也是有序的。

    public static void insertSort(int[] data) {
        int length = data.length;
        for (int i = 0; i < length; i++) {
            for (int j = i - 1; j >= 0 && data[j + 1] < data[j]; j--) {
                swap(data, j + 1, j);
            }
        }
    }

归并排序

排好左右两边子数组的顺序，然后利用额外临时空间合并回原数组。

将数组二分直到只有一个数为止，然后进行归并，这里采用了递归的方法。递归分解到下图，类似二叉树，然后采用类似中序遍历的执行路径。

创建一个左边数组+右边数组大小的临时数组，然后循环左右比较，将较小的值放到临时数组直到越界，将剩下的数组拷贝到临时数组，最后拷贝回数组，下面是图解。

    public static void mergerSort(int[] data, int l, int r) {
        if (l == r) {
            return;
        }
        int m = l + (r - l >> 1);
        mergerSort(data, l, m);
        mergerSort(data, m + 1, r);
        merger(data, l, r, m);
    }

    private static void merger(int[] data, int l, int r, int m) {
        int[] temp = new int[r - l + 1];
        int i = 0;
        int p1 = l, p2 = m + 1;
        while (p1 <= m && p2 <= r) {
            temp[i++] = data[p1] < data[p2] ? data[p1++] : data[p2++];
        }
        while (p1 <= m) {
            temp[i++] = data[p1++];
        }
        while (p2 <= r) {
            temp[i++] = data[p2++];
        }
        // l左边为已经排序好的数组
        int length = temp.length;
        for (int j = 0; j < length; j++) {
            data[l + j] = temp[j];
        }
    }

快速排序

将数组调整为>n、=n、<n三个部，然后对两边一直调整直到只剩下一个数。

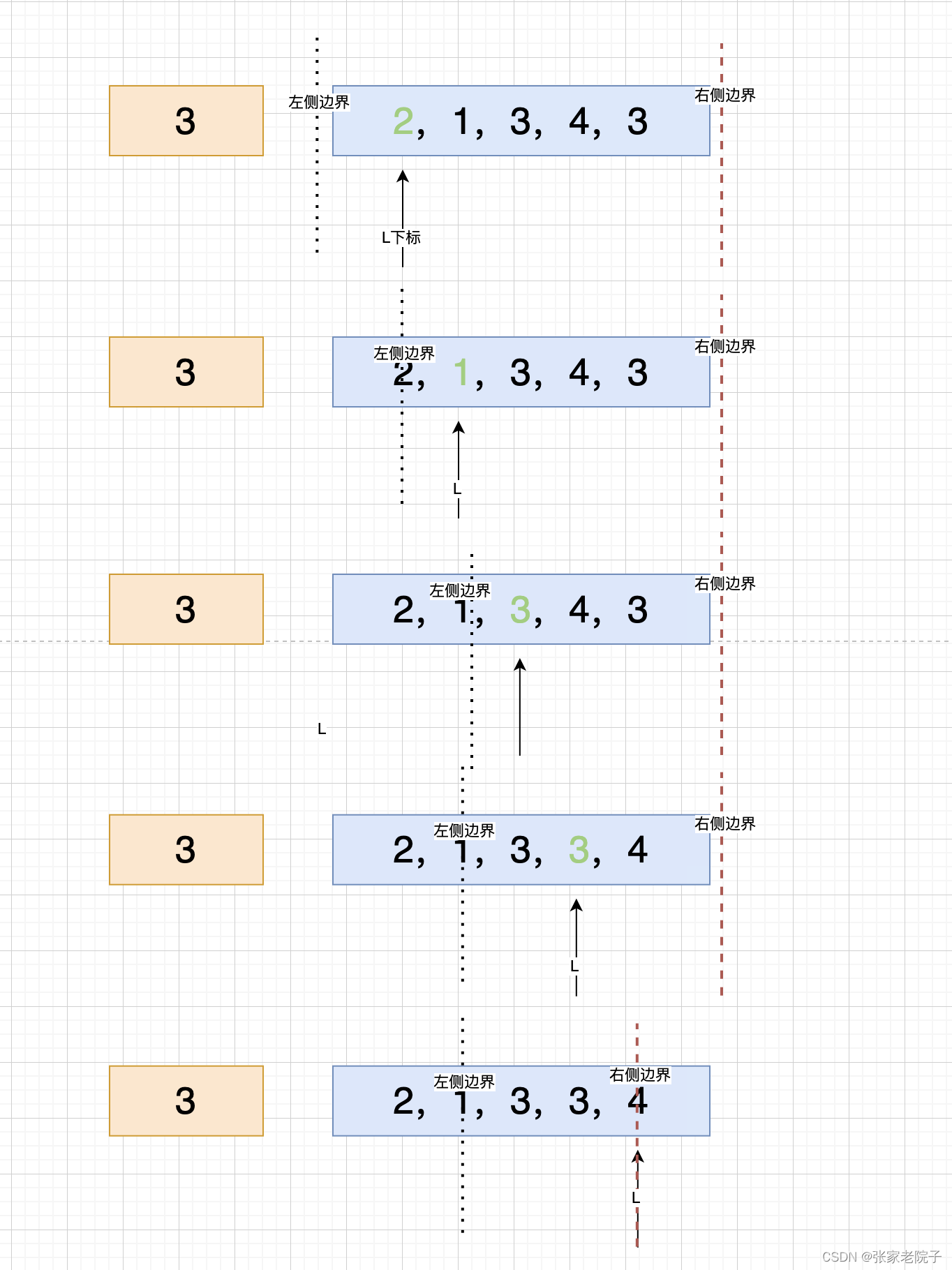
选取最后一个数3为基准，小于3的放左边，大于3的放右边。然后对左右两边采用同样的方法，右边得到4，只有一个数左右两边相等，直接结束。左边 2，1，选取1位基准，然后把2放到右边。此时的数组顺序就排列好了。

swap(data, l + (int) (Math.random() * (r - l + 1)), r) 代码是随机选取一个数放到最后作为基准，根据概率统计学得出能减小时间复杂度结论。

partition的过程就是和基准值比较，小于基准值左边界+1，下标+1；等于基准值，下标+1；大于基准值交换值，右边界-1。

   public static void quickSort(int[] data, int l, int r) {
        if (l < r) {
            swap(data, l + (int) (Math.random() * (r - l + 1)), r);
            int[] p = partition(data, l, r);
            quickSort(data, l, p[0] - 1);
            quickSort(data, p[1] + 1, r);
        }
    }

    private static int[] partition(int[] data, int l, int r) {
        //l 遍历的下标
        int less = l - 1; //左侧边界
        int more = r; //右侧边界
        while (l < more) {
            if (data[l] < data[r]) {
                swap(data, ++less, l++);
            } else if (data[l] > data[r]) {
                swap(data, l, --more);
            } else {
                l++;
            }
        }
        swap(data, more, r);
        return new int[]{less + 1, more};
    }

堆排序

调整构造一个大顶堆，每次取出根节点放到数组最后，然后调整堆符合大顶堆结构，取出根节点重复直到堆没有元素。

大顶堆采用数组下标关系构建，其实是一个虚拟的结构，真实结构是数组，跟据下标来确定父子的位置。例如i位置为根节点，那么2i+1为左子节点，2i+2为右子节点，且根节点最大，次大在左右子节点中。

整个流程如下图：

    public static void heapSort(int[] data) {
        //构造大顶堆
        int length = data.length;
        int heapSize = length;
        for (int i = length - 1; i >= 0; i--) {
            heapify(data, i, heapSize);// O(logN)
        }
        while (heapSize > 0) {// O(N)
            heapify(data, 0, heapSize);// O(logN)
            swap(data, 0, --heapSize); // O(1) 取出大顶堆的根节点放到数组后面
        }
    }

    /**
     * 堆调整
     * 获取左右节点较大值，如果比当前值小就交换
     *
     * @param data
     * @param index
     * @param heapSize
     */
    private static void heapify(int[] data, int index, int heapSize) {
        int left = 2 * index + 1;
        while (left < heapSize) {
            //获取子节点较大的值
            int largest = left + 1 < heapSize && data[left + 1] > data[left] ? left + 1 : left;
            largest = data[largest] > data[index] ? largest : index;
            if (largest == index) break;
            //交换当前值和最大值
            swap(data, largest, index);
            index = largest;
            left = 2 * index + 1;
        }
    }

总结

算法	时间复杂度	空间复杂度	稳定性
插入排序	O(N^2)	S(1)	Yes
选择排序	O(N^2)	S(1)	No
冒泡排序	O(N^2)	S(1)	Yes
归并排序	*O(NlogN)**	S(N)	Yes
快速排序	*O(NlogN)**	S(logN)	No
堆排序	*O(NlogN)**	S(1)	No