二叉搜索树

二叉搜索树的结构

二叉树的性质：
性质一：在二叉树的i层上至多有2 i-1个节点（i>=1）至少有1个
性质二：深度为k的二叉树至多有2k-1个节点，至少为k个
性质三：对任何一棵二叉树T，如果终端结点树为n，度为2的结点为n2,度为0的结点为n0 则n0=n2+n1
性质四：具有n个节点的完全二叉树的深度为[log2n]+1向下取整
性质五：如果有一颗有n个节点的完全二叉树的节点按层次序编号，对任一层的节点i（1<=i<=n）有

1. 如果i=1，则节点是二叉树的根，无双亲，如果i>1，则其双亲节点为[i/2]，向下取整
2. 如果2i>n那么节点i没有左孩子，否则其左孩子为2i
3. 如果2i+1>n那么节点没有右孩子，否则右孩子为2i+1

二叉搜索树能够高效的处理一下操作：
- 插入一个数值
- 查询是否包含某个数值
- 删除某个数值

二叉搜索树存储数据的方法：
任意节点左子树上的所有节点都比自己小，而右子树上的所有节点都比自己大。
如下图为一个二叉搜索树

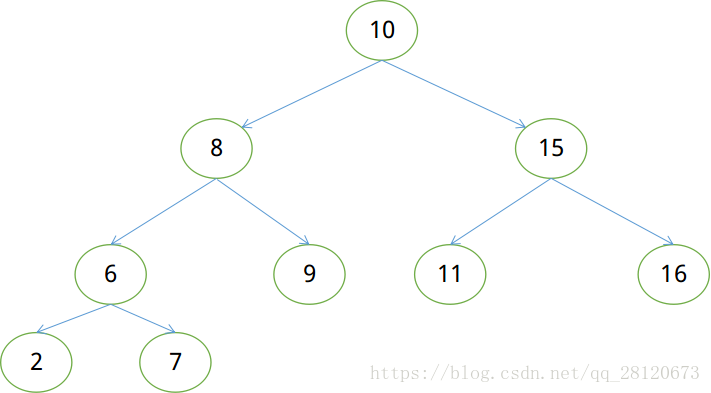
在二叉搜索树中查找和插入操作都从树的顶端开始比较，如果比当前节点小则搜索左子树，比当前节点大则搜索右子树。最多比较此时为二叉树的高度。
在二叉搜索树中查询和插入比较简单，那么要怎么删除数据呢？
如果删除的是叶子节点，那么操作比较简单。
一般需要根据下面的情况进行处理：

• 要删除的节点没有左孩子，那么把右孩子提上去
• 需要删除的节点的左孩子没有右孩子，那么把左孩子提上去，右孩子作为左孩子的左孩子的右孩子
• 以上都不满足的话，就把做左儿子的子孙中最大的节点提到需要删除的节点上

二叉搜索树的复杂度

二叉搜索树的搜索时间与层数成正比，如果有n个元素，品均每次操作的时间为$O(logn)$。

二叉搜索树的实现

代码如下：

#include <iostream>

using namespace std;

struct node {
    int val;
    node *lch, *rch;
};

//插入数值
node *insert(node *p, int x) {
    if (p == nullptr) {
        node *q = new node;
        q->val = x;
        q->lch = nullptr;
        q->rch = nullptr;
        return q;
    } else {
        if (p->val > x) {
            p->lch = insert(p->lch, x);
        } else if (p->val < x) {
            p->rch = insert(p->rch, x);
        }
    }
    return p;
}

//删除数值
node *remove(node *p, int x) {
    if (p == nullptr) {
        return nullptr;
    } else if (x < p->val) p->lch = remove(p->lch, x);
    else if (x > p->val) p->rch = remove(p->rch, x);
    else if (p->lch == nullptr) {
        node *q = p->rch;
        delete p;
        return q;
    } else if (p->lch->rch == nullptr) {
        node *q = p->lch;
        node *u = p->rch;
        delete p;
        q->rch = u;
        return q;
    } else {
        node *q;
        for (q = p->lch; q->rch->rch != nullptr; q = q->rch);
        node *r = q->rch; //r为要移动的节点,r没有右孩子
        node *u = r->lch; //u为r的左孩子
        q->rch = u;          //将r的左孩子接在r的位置上
        r->lch = p->lch;
        r->rch = p->rch;
        return p;
    }
}

//查找
bool find(node *p, int x) {
    if (p == nullptr) {
        return false;
    }
    if (p->val == x) {
        return true;
    } else if (p->val > x) {
        return find(p->lch, x);
    } else {
        return find(p->rch, x);
    }

}

在实际的使用中我们一般不自己构造二叉搜索树，c++的STL标库中的set容器就是使用的二叉搜索树来实现的