归并排序法（Merge Sort）

归并排序法（Merge Sort）：归并排序是建立在归并操作上的一种有效的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有的子序列合并，得到完全有序的
序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为“二路归并”。

归并排序是“稳定的排序”，即相等的元素的顺序不会发生改变。
特点：
1. 归并排序速度“仅次于“快速排序（不稳定）””，为稳定排序算法，一般用于对总体无序，但各子项相对有序的数列。
2. 归并排序的比较次数小于快速排序的比较次数，移动次数一般多于快速排序的移动次数！！！

归并排序的时间复杂度为：nlogn, 最好和最差都是nlogn。 //稳定的！！！！

归并排序的思路：
1. 对于一组数列，先将相邻两个数字进行归并操作（merge），形成floor(n/2)个序列，排序后每个序列包含两个元素（可能也为1个元素）
2. 将1序列的子序列再次归并，形成floor(n/4)个序列，排序后每个序列包含4个元素(可能为3个元素（奇数数列时）)。
3. 重复2，知道所有子序列合并成一个序列

代码如下：
/*
Des: 归并算法： 用于归并两个子序列
Param: array 排列数组
Param: start_1 第一列子段的初始位置
Param: end_1 第一列子段的末位置
Param: start_2 第二列子段的初始位置
Param: end_2 第二列子段的末位置
Param: size 整个数组的长度
*/
template
void Merge(T array[], int start_1, int end_1, int start_2, int end_2, int size)
{
if (start_2 >= size)
{
return;
}

//定义一个临时的缓存数组，用于存放归并后的值
int length = end_2 - start_1 + 1;
T* tempArray = new T[length];
memset(tempArray, 0, length * sizeof(T));

//先定义一个数组，长度为end_1-start_1，用于存放排序后的值
memset(tempArray, 0, sizeof(T)*length);

//比较两子序列，将较小值先放于临时数组
int x = start_1;    //用于标记序列1中剩余元素的起始下标
int y = start_2;    //用于标记序列2中剩余元素的起始下标
int index_temp = 0;     //用于标记temp已记录的数量

while ((y <= end_2) && (y < size) && (x <= end_1))
{
    if (array[x] <= array[y])
    {
        tempArray[index_temp++] = array[x++];
    }
    else
    {
        tempArray[index_temp++] = array[y++];
    }
}

//检测是否还有未加到临时数组的元素，加入到临时数组中
if (x <= end_1)
{
    while (x <= end_1)
    {
        tempArray[index_temp++] = array[x++];
    }
}
else if (y <= end_2)
{
    while ((y <= end_2) && (y < size))
    {
        tempArray[index_temp++] = array[y++];
    }
}

//将排序好的临时数组的变量copy到array中
for (int i = start_1; i<=end_2; i++)
{
    if (i >= size)
    {
        break;
    }

    array[i] = tempArray[i - start_1];
}

delete[] tempArray;
tempArray = NULL;

}

/*
Des：Merge Sort
Param: array 排序数组
Param: size 要排序的长度
*/
template
void MergeSort(T array[], int size)
{
if ((array == NULL) || (size <= 1))
{
return;
}

//先进行最小子序列排序
int startIndex = 0;
int endIndex = startIndex + 1;
while (endIndex < size)
{
    if (array[startIndex] > array[endIndex])
    {
        T temp = array[startIndex];
        array[startIndex] = array[endIndex];
        array[endIndex] = temp;
    }

    startIndex = endIndex + 1;
    endIndex = startIndex + 1;
}

//合并子序列
int n = 2;  //子序列的长度
int start_1 = 0;
int end_1 = start_1 + n - 1;
int start_2 = end_1 + 1;
int end_2 = start_2 + n - 1;
while (start_2 < size)
{
    int tempStart_1 = start_1;
    int tempEnd_1 = end_1;
    int tempStart_2 = start_2;
    int tempEnd_2 = end_2;
    while (tempStart_2 < size)
    {
        Merge(array, tempStart_1, tempEnd_1, tempStart_2, tempEnd_2, size);

        tempStart_1 = tempEnd_2 + 1;
        tempEnd_1 = tempStart_1 + n - 1;
        tempStart_2 = tempEnd_1 + 1;
        tempEnd_2 = tempStart_2 + n - 1;
    }

    n = n * 2;
    start_1 = 0;
    end_1 = start_1 + n - 1;
    start_2 = end_1 + 1;
    end_2 = start_2 + n - 1;
}

}

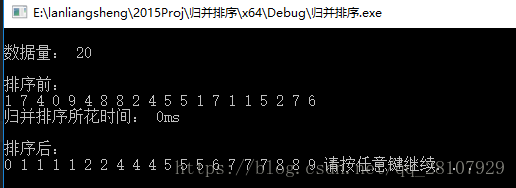
实现结果：