众包中的上下文感知结果推理

作者

Yili Fang${}^{a,b}$, Hailong Sun${}^{a,b}$, ∗, Guoliang Li${}^c$ , Richong Zhang${}^{a,b}$, Jingpeng Huai${}^{a,b}$
${}^a$SKLSDE Lab, School of Computer Science and Engineering, Beihang University, Beijing 100191, China
${}^b$Beijing Advanced Innovation Center for Big Data and Brain Computing, Beijing 100191, China
${}^c$Department of Computer Science, Tsinghua University, Beijing, China

摘要

针对众包质量控制问题，提出了多种结果推理方法。然而，现有的方法对于上下文敏感任务（Context-Sensitive Task，CST）无效，例如手写识别、翻译、语音转录，因为两个原因不能忽略任务中的上下文关联。首先，由于要正确完成一个复杂的任务相当困难，因此将整个$\mathrm{C}\mathrm{S}\mathrm{T}$（如识别手写文本）挤在一起并使用任务级推理方法来推理答案是无效的。其次，虽然$\mathrm{C}\mathrm{S}\mathrm{T}$由一组原子子任务组成（例如，识别手写字），但不适合将其拆分为多个子任务，并采用子任务级推理算法来推理结果，因为这样会丢失子任务之间的上下文关联性（例如，短语），增加完成任务的难度。因此，它需要一种处理$\mathrm{C}\mathrm{S}\mathrm{T}$的新方法。本文研究了$\mathrm{C}\mathrm{S}\mathrm{T}$的结果推理问题，提出了一种上下文感知的推理算法。结合上下文信息，设计了一种推理算法。此外，我们还引入了一种迭代的方法来提高质量。在实际$\mathrm{C}\mathrm{S}\mathrm{T}$上的实验结果表明，我们的方法与目前最先进的方法相比具有优越性。

1 介绍

众包旨在利用群体的智慧来解决计算机难以解决的问题[2]。在许多应用中，特别是在数据管理[25]领域，其成功表现在从简单任务（如图像标记[10,21]和实体分辨[38]）到复杂任务（如文本编辑[4]和软件开发[19]）的各种应用中。

由于工人可能返回噪音结果，众包的核心问题是确保结果质量[25]。结果推理是一种广泛采用的控制质量的方法，它首先将每个任务分配给多个工人，然后使用推理算法对分配的工人的结果进行汇总。以图像标签为例。图像被分配给多个工人，他们将提供描述图像内容的标签。最后的结果是通过投票[40]或其他推理方法[41]从所有收集的标签中选择标签的子集。

在众包中，有一个重要的任务类别，由一组上下文关联的子任务组成，例如手写识别[7]、翻译[47]、路线规划[45]和音频转录[34]。在这项工作中，我们称这种众包任务为上下文敏感的任务（即$\mathrm{C}\mathrm{S}\mathrm{T}$）。例如，图1(a)显示了手写识别的示例，要求工人识别由多个单词组成的手写句子。一个句子中的词在对应句子所确定的一致语义环境中有着密切的联系。因此手写识别是一种典型的$\mathrm{C}\mathrm{S}\mathrm{T}$。然而，对于结果推理，现有的方法对于上下文敏感任务（$\mathrm{C}\mathrm{S}\mathrm{T}$）并不有效。一方面，$\mathrm{C}\mathrm{S}\mathrm{T}$相当困难，每个工人都无法正确回答整个任务（例如，正确识别一个句子中的所有单词用于手写识别任务）。图1(b)说明了三个工人给出的答案，每个答案都是完全或部分被认可的句子。任何工人都不能正确识别这个句子。因此，对于任务级推理算法[18,38,48]，它将每个完整任务分配给不同的工人，并汇总每个任务的答案，很难从单个工人那里获得高质量的答案。另一方面，每个任务在其子任务之间都有内部上下文关联。例如，一个句子中的单词不是独立的，它们在上下文中相互关联。显然，在结果推理中不能忽略上下文。例如，单词3-5的第二个答案是“misspelled several words”，而第三个答案是“misspelled several works”。显然，第二个答案更为合理，因为“misspelled”与“several words”比“several works”更为密切关联。此外，假设另一个工人将单词3-5识别为“拼写错误的多个作品”。如果忽略上下文关联，基于投票的推理可能会将“misspelled several works”视为最终结果，这显然是错误的。因此，子任务级推理算法[4,38,44]将每个任务拆分为多个子任务，并从工作人员那里聚合每个子任务的答案，也不有效。因此，这两种方法都不适用于$\mathrm{C}\mathrm{S}\mathrm{T}$，因为它们不使用上下文关联来共同考虑结果推理中已识别的答案。

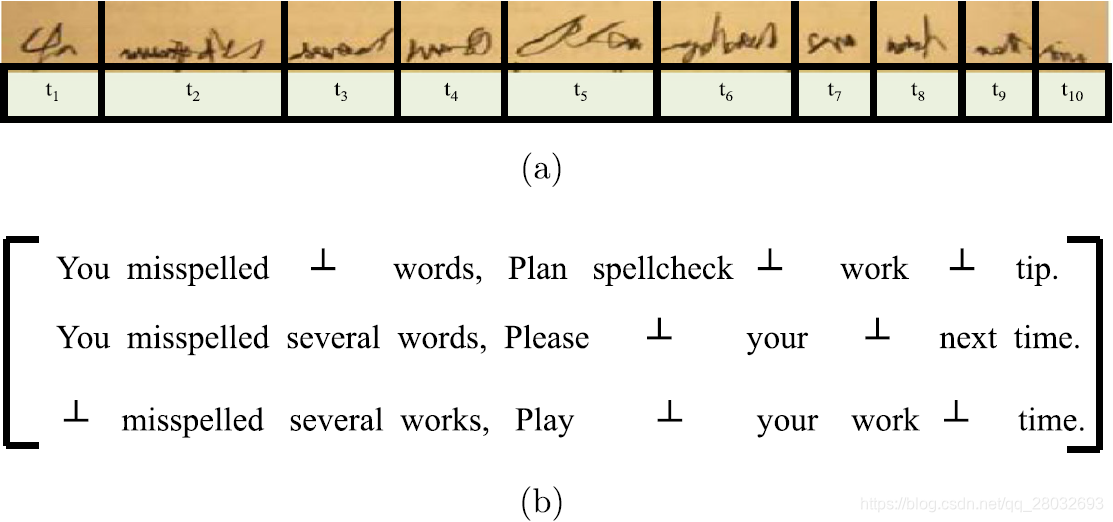
图1. CST任务 (a)手写识别任务 (b)三名工人提供的答案

处理$\mathrm{C}\mathrm{S}\mathrm{T}$有两个主要挑战。

• 首先，捕获上下文关联是非常重要的，因为$\mathrm{C}\mathrm{S}\mathrm{T}$通常不包含足够的信息。这就带来了一个挑战，即对上下文关联进行建模，用稀疏信息解决模型，并推理出高质量的答案。
• 第二，$\mathrm{C}\mathrm{S}\mathrm{T}$比简单的任务更复杂，一次迭代通常无法获得高质量的结果。为了解决这两个难题，

我们研究了两个问题：结果推理和迭代决策。前者的目的是从工人提交的答案中推理出最佳结果，后者主要检查推理结果是否可以进一步改进：如果结果足够好，迭代过程将终止；否则将开始新的迭代。

在这项工作中，我们提出了一种上下文感知的推理方法来提高$\mathrm{C}\mathrm{S}\mathrm{T}$的质量。首先，我们使用隐马尔可夫模型（HMM）[15,33]来描述上下文关联和设计上下文感知推理算法（Context-Inf）。特别是，我们结合外部知识来解决缺乏上下文关联信息的挑战。然后，我们建议使用上下文信息支持众包的迭代改进。综上所述，我们做出如下贡献：

• 我们确定了众包任务的一个重要类别，即上下文敏感任务（$\mathrm{C}\mathrm{S}\mathrm{T}$）。据我们所知，这是第一次尝试研究上下文感知推理。
• 我们建立了一个描述$\mathrm{C}\mathrm{S}\mathrm{T}$众包过程的概率模型，提出了将HMM与外部知识结合到MLE和EM算法中的上下文信息来推理结果。
• 对于复杂的$\mathrm{C}\mathrm{S}\mathrm{T}$，我们设计了一个基于$\mathrm{P}\mathrm{O}\mathrm{M}\mathrm{D}\mathrm{P}$的迭代决策模型来提高质量。
• 我们对两种$\mathrm{C}\mathrm{S}\mathrm{T}$进行了广泛的实验：手写识别和音频转录。实验结果表明了该方法的优越性。

2 问题公式化

在本节中，我们首先介绍表1中所用的符号，并将本文研究的主要问题公式化。上下文敏感任务（$\mathrm{C}\mathrm{S}\mathrm{T}$）包含多个子任务，这些子任务与特定上下文关联。关键问题是尽可能地推理出高质量$\mathrm{C}\mathrm{S}\mathrm{T}$的结果。如果拆分（$\mathrm{C}\mathrm{S}\mathrm{T}$）的这些子任务，则上下文将丢失。例如，图1(a)显示了一个上下文敏感的任务，即手写识别。如果将手写句子拆分为10个子任务（如单词），则由于上下文关联性的丢失，识别难度会增加。

表1.符号说明

符号	描述
$\mathcal{A}$	HMM的状态转移矩阵
$\mathcal{B}$	HMM的输出概率矩阵
$\pi$	HMM的初始状态概率
$\lambda$	隐马尔可夫模型$\lambda =(\mathcal{A},\mathcal{B},\pi )$
$\mathrm{T}$	一个上下文敏感任务
${\mathrm{T}}^{\prime }$	一个带有真值标签的测试任务
$o_{ij}^{\mathrm{T}}$	工人$i$提交的$\mathrm{T}$的子任务$j$的输出
$O^{\mathrm{T}}$	$\mathrm{C}\mathrm{S}\mathrm{T}\mathrm{T}$的输出矩阵 O T = { o i j T } O^T=\{o_{ij}^T\} OT={oijT​}
$K_j^{\mathrm{T}}$	子任务$j$的候选回答集合
$k_{ij}^{\mathrm{T}}$	子任务$j$在$\mathrm{T}$中的第$i$个候选答案
$z_j^{\mathrm{T}}$	子任务$j$的真值标签
$Z^{\mathrm{T}}$	$\mathrm{C}\mathrm{S}\mathrm{T}\mathrm{T}$的真值标签
$\Gamma$	测试任务集合 Γ = { ( T ′ , Z T ′ ) } \Gamma=\{(\mathrm{T'},Z^{\mathrm{T'}})\} Γ={(T′,ZT′)}
${\mathrm{C}}_{\mathrm{T}}$	$\mathrm{C}\mathrm{S}\mathrm{T}\mathrm{T}$的一个候选输出向量
${\mathcal{C}}^{\mathrm{T}}$	所有可能$\mathrm{C}\mathrm{O}\mathrm{V}$的集合 C T = { C T } \mathcal{C}^\mathrm{T}=\{\mathrm{C_T}\} CT={CT​}
$d_j^{\mathrm{T}}$	子任务的难度$d_j^{\mathrm{T}}\in [0,1]$
$D^{\mathrm{T}}$	$\mathrm{C}\mathrm{S}\mathrm{T}$的难度 D T = { d j T } D^\mathrm{T}=\{d_j^\mathrm{T}\} DT={djT​}
$w_i^{\mathrm{T}}$	准确度参数$w_i\in [1,+\infty ]$
$W^{\mathrm{T}}$	回答$\mathrm{T}$的工人准确度参数集合
$c_{\mathrm{T}}^l$	$\mathrm{C}\mathrm{S}\mathrm{T}\mathrm{T}$的第$l$个$\mathrm{C}\mathrm{O}\mathrm{V}$
$sim(k_{ij}^{\mathrm{T}},k_{i^{\prime }j}^{\mathrm{T}})$	候选结果$k_{ij}^{\mathrm{T}}$和$k_{i^{\prime }j}^{\mathrm{T}}$之间的原始相似度
$\theta (k_{i^{\prime \prime }j}^{\mathrm{T}},k_{i^{\prime }j}^{\mathrm{T}})$	两个错误结果$k_{i^{\prime \prime }j}^{\mathrm{T}}$和$k_{i^{\prime }j}^{\mathrm{T}}$之间的归一化距离
$\delta$	一个克罗内克函数（Kronecker Delta Function）
$l_{{\mathrm{T}}^{\prime }}$	一个测试任务${\mathrm{T}}^{\prime }$的对数似然函数
$L_{\Gamma }$	一个测试任务集合$\Gamma$的对数似然函数
$P^{k_{ij}^{\mathrm{T}}}$	$k_{ij}^{\mathrm{T}}$是正确结果的概率
$Q$	EM算法的辅助函数
$b_{k_{ij}}(O_{\ast j})$	$\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$模型的输出概率

给定一个带有$m$个子任务的$\mathrm{C}\mathrm{S}\mathrm{T}\mathrm{T}$，每个子任务分配给$n$个工人，我们使用一个输出矩阵来表示这些工人的答案。

定义1（输出矩阵，Output Matrix)。$n$个工人对于$\mathrm{T}$的回答表示为一个$n\times m$矩阵，$O^{\mathrm{T}}=(o_{ij}^{\mathrm{T}}{)}_{n\times m}$，其中$o_{ij}^{\mathrm{T}}$是工人$i$对子任务$j$的输出，如果工人$i$没有提供子任务$j$输出，则$o_{ij}^{\mathrm{T}}=\perp$，我们用$O_{\ast j}^{\mathrm{T}}$表示子任务$j$的输出向量，用$O_{i\ast }^{\mathrm{T}}$表示工人$i$的输出向量。

注意，当且仅当工人$i$无法处理子任务$j$时$o_{ij}^{\mathrm{T}}$是$\perp$。例如，图1(b)说明了图1(a)中手写识别$\mathrm{C}\mathrm{S}\mathrm{T}\mathrm{T}$的输出矩阵。$o_{31}^{\mathrm{T}}=\perp$因为第三个工人不能识别第一个词。为了生成$\mathrm{T}$的推理结果，我们定义了候选输出向量来表示推理结果。

定义2（候选输出向量，Candidate Output Vector–COV)。$O_{\ast j}^{\mathrm{T}}$表示子任务$j$的输出向量。 K j T = { k i j T = o i j T ∣ o i j T ∈ O ∗ j T } K_j^\mathrm{T}=\{ k_{ij}^\mathrm{T}=o_{ij}^\mathrm{T}|o_{ij}^\mathrm{T}\in O_{*j}^\mathrm{T}\} KjT​={kijT​=oijT​∣oijT​∈O∗jT​}表示子任务$j$的不同结果的集合。${\mathrm{C}}_{\mathrm{T}}=⟨k_{i_{1}1}^{\mathrm{T}},...k_{i_{j}j}^{\mathrm{T}},...,k_{i_{m}m}^{\mathrm{T}}⟩$表示一个候选输出向量，其中$k_{i_{j}j}^{\mathrm{T}}\in K_j^{\mathrm{T}}$是子任务$j$的一个结果。

注意，$O_{\ast j}^{\mathrm{T}}$是子任务$j$的结果向量,$K_j^{\mathrm{T}}$是子任务$j$的不同结果的集合，表2说明了图1(b)中输出矩阵$O^{\mathrm{T}}$的所有12个$\mathrm{C}\mathrm{O}\mathrm{V}$，其中$c_{\mathrm{T}}^l$是$\mathrm{C}\mathrm{S}\mathrm{T}\mathrm{T}$（手写识别）的第$l$个$\mathrm{C}\mathrm{O}\mathrm{V}$.接下来，我们将$\mathrm{C}\mathrm{S}\mathrm{T}$的结果推理问题转化为识别最佳$\mathrm{C}\mathrm{O}\mathrm{V}$的问题。

表2.一个手写识别任务的COV

$c_{\mathrm{T}}^1$	You misspelled several work, Plan spellcheck your work next tip.
$c_{\mathrm{T}}^2$	You misspelled several work, Plan spellcheck your work next time.
$c_{\mathrm{T}}^3$	You misspelled several work, Please spellcheck your work next tip.
$c_{\mathrm{T}}^4$	You misspelled several work, Please spellcheck your work next time.
$c_{\mathrm{T}}^5$	You misspelled several work, Play spellcheck your work next tip.
$c_{\mathrm{T}}^6$	You misspelled several work, Play spellcheck your work next time.
$c_{\mathrm{T}}^7$	You misspelled several words, Plan spellcheck your work next tip.
$c_{\mathrm{T}}^8$	You misspelled several words, Plan spellcheck your work next time.
$c_{\mathrm{T}}^9$	You misspelled several words, Please spellcheck your work next tip.
$c_{\mathrm{T}}^{10}$	You misspelled several words, Please spellcheck your work next time.
$c_{\mathrm{T}}^{11}$	You misspelled several words, Play spellcheck your work next tip.
$c_{\mathrm{T}}^{12}$	You misspelled several words, Play spellcheck your work next time.

定义3（识别最佳COV，Identifying the Best COV–ICOV）。 设$\mathrm{T}$为$\mathrm{C}\mathrm{S}\mathrm{T}$，$O^{\mathrm{T}}$为$\mathrm{T}$的输出矩阵，${\mathcal{C}}^{\mathrm{T}}$为所有可能的$\mathrm{C}\mathrm{O}\mathrm{V}$的集合，设 p { C T ∣ T , O T } p\{\mathrm{C_T}|\mathrm{T},O^\mathrm{T}\} p{CT​∣T,OT}表示${\mathrm{C}}_{\mathrm{T}}$为正确输出的概率，则问题是从${\mathrm{C}}_{\mathrm{T}}$中找到最佳$\mathrm{C}\mathrm{O}\mathrm{V}$，如下所示：

C T ′ = arg ⁡ max ⁡ C T ∈ C T p { C T ∣ T , O T } . (1) \mathrm{C'_T}={\arg\max}_{\mathrm{C_T}\in \mathcal{C}^\mathrm{T}}p\{\mathrm{C_T}|\mathrm{T},O^\mathrm{T}\}.\tag{1} CT′​=argmaxCT​∈CT​p{CT​∣T,OT}.(1)

例如，用图1(b)中的$O^{\mathrm{T}}$装配最佳结果等于从表2中的$\mathrm{C}\mathrm{O}\mathrm{V}$集合中选择最佳$\mathrm{C}\mathrm{O}\mathrm{V}$。我们将讨论如何计算概率 p { C T ∣ T , O T } p\{\mathrm{C_T}|\mathrm{T},O^\mathrm{T}\} p{CT​∣T,OT}，并在第4节中确定最佳$\mathrm{C}\mathrm{O}\mathrm{V}$。

为了提高推理质量，广泛采用迭代法来决定何时终止众包过程。

定义4（迭代决策问题，Iterative Decision Problem–IDP）。 设$\mathrm{T}$为$\mathrm{C}\mathrm{S}\mathrm{T}$，$O^{\mathrm{T}}$为$\mathrm{T}$的输出矩阵，$c_{\mathrm{T}}$和$c_{\mathrm{T}}^{\prime }$分别为当前迭代和上一次迭代的推理结果。IDP问题是确定是否终止迭代过程。

定义4定义了一个迭代地获得满意的CST推理结果的决策问题，我们在第5节描述了我们的方法。

讨论。 根据定义2，在最坏的情况下，可以有$n^m$个$\mathrm{C}\mathrm{O}\mathrm{V}$。理论上，$\mathrm{C}\mathrm{O}\mathrm{V}$集的大小随子任务的数量呈指数增长，定义3中的$\mathrm{I}\mathrm{C}\mathrm{O}\mathrm{V}$问题是一个NP难问题[52]。然而，正如在[7]中提到的，由于$\mathrm{C}\mathrm{S}\mathrm{T}$的大小有限，并且工人重复子任务结果，$\mathrm{C}\mathrm{O}\mathrm{V}$的状态空间很小。例如，在表2中，手写识别任务的$\mathrm{C}\mathrm{O}\mathrm{V}$大小仅为12，远远小于理论值（即310）。

3 上下文感知的众包框架

在本节中，我们概述了我们的CST上下文感知众包框架，如图2所示，其中任务生成、结果推理和迭代决策是三个主要步骤。

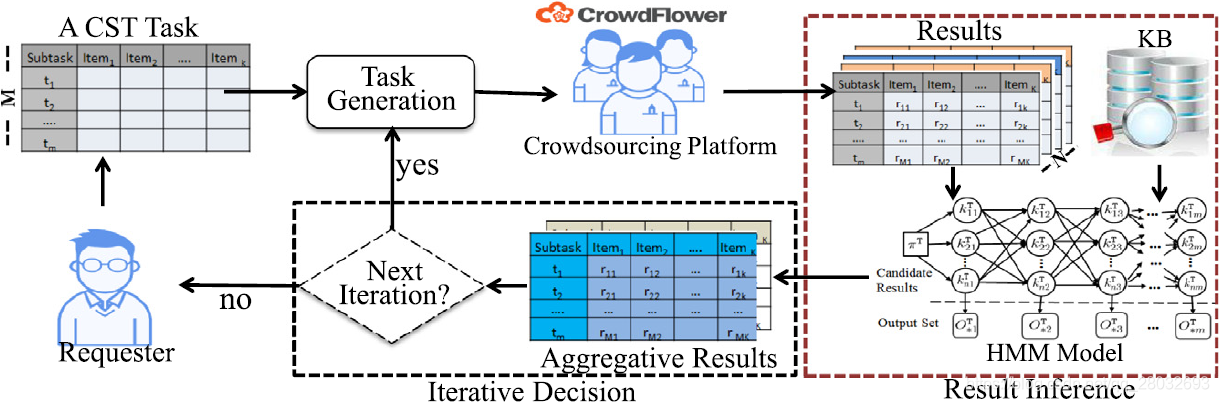
图2. 我们的上下文感知众包概述

任务生成。 我们首先将每个任务分成一系列子任务。例如，我们可以使用OpenCV${}^1$将手写识别任务拆分为单词序列，如图1(a)所示。然后，我们将整个任务众包给人群，并要求工人按顺序回答子任务的顺序，最后，我们收集答案。

结果推理。 此步骤旨在对每个$\mathrm{C}\mathrm{S}\mathrm{T}$进行结果推理。我们建立了一个概率模型来描述工人的绩效。然后，我们用HMM模型[15]对上下文关联进行建模，并将HMM推理算法引入到EM算法中。为了了解HMM的参数，我们从外部知识库中获取信息。

迭代决策。 我们使用迭代改进方法，在下一轮中，工人将改进当前轮的结果。

我们认为，这种框架一般用于处理各种$\mathrm{C}\mathrm{S}\mathrm{T}$，也可用于两种典型的众包场景：有和无黄金测试（Golden Tests）。对于没有黄金测试的情况，请求者提交一组任务$\mathcal{T}$集合；对于有黄金测试，除了$\mathcal{T}$之外，请求者还提交一组具有已知真值标签$\Gamma$的任务，其中 Γ = { ( T ′ , Z T ′ ) ∣ T ′ \Gamma=\{(\mathrm{T'},Z^{\mathrm{T'}})|\mathrm{T'} Γ={(T′,ZT′)∣T′是黄金测试任务，$Z^{{\mathrm{T}}^{\prime }}$是${\mathrm{T}}^{\prime }$的真值标签$\}$。我们主要使用EM算法和MLE算法来学习未知参数。因为在EM算法中，推理结果与实际情况不绝对完全一致。最大似然估计（MLE）中的真值标签是预先知道的。因此，EM算法得到的参数精度低于MLE算法得到的参数精度。因此，在我们的工作中，$\Gamma$和$\mathcal{T}$是混合在一起的，工人不知道哪些是黄金测试任务。$\Gamma$用MLE估计工人的准确度，然后用EM算法推理出$\mathrm{T}\in \mathcal{T}$的最佳$\mathrm{C}\mathrm{O}\mathrm{V}$和任务难度。每项任务$\mathrm{T}\in \mathcal{T}$和${\mathrm{T}}^{\prime }\in \Gamma$将分配给$N$个工人。一旦工人完成了他们的任务，根据对测试任务的评估，将淘汰质量较低的输出。不同之处在于对$\Gamma$，我们可以使用MLE来推理参数。

4 CST的上下文感知推理

本节主要介绍两种解决$\mathrm{I}\mathrm{C}\mathrm{O}\mathrm{V}$问题的方法。

4.1 模拟子任务的众包过程

本小节模拟了子任务的众包过程。基于上述讨论，受Whitehill等人[46]的启发，我们给出了图3所示的图形模型。

工人$i$在$\mathrm{T}$中提交子任务$j$的输出$o_{ij}^{\mathrm{T}}$主要取决于三个因素：

1. 子任务的难度$d_j^{\mathrm{T}}\in [0,1]$。一般来说，$d_j^{\mathrm{T}}$越高任务越难。
2. 工人$i$提交的结果的准确度：$w_i^{\mathrm{T}}\in [1,+\infty ](1/w_i^{\mathrm{T}}\in [0,1])$，表示准确度的倒数，较小的$w_i^{\mathrm{T}}$是指工人$i$提交的结果更准确；（请注意，为了简明地模拟我们的模型，我们使用准确度的倒数，见公式(2)）。
3. 子任务$j$的真值标签$z_j^{\mathrm{T}}$。然后，我们可以给出一个概率模型来模拟回答过程。

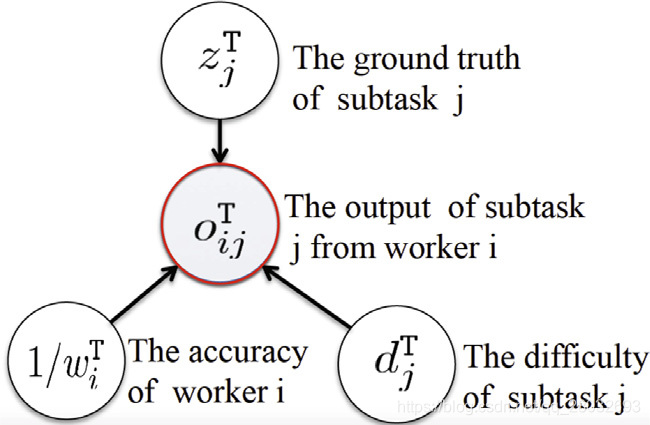
图3. $\mathrm{C}\mathrm{S}\mathrm{T}\mathrm{T}$的子任务$j$的概率图模型

首先，我们建立工人回答正确的概率模型。我们的直觉是，生成正确答案的概率取决于三个因素：任务难度、工人的准确度以及在候选答案集中正确答案的分布。假设$k_{i^{\prime }j}^{\mathrm{T}}\in K_j^{\mathrm{T}}$是子任务$j$的正确答案。如果工人$i$给出了子任务$j$的正确答案，即$o_{ij}^{\mathrm{T}}=k_{i^{\prime }j}^{\mathrm{T}}$，那么工人i的输出$o_{ij}^{\mathrm{T}}$是子任务$j$的正确答案的概率定义如下：

$$P(o_{ij}^{\mathrm{T}}=k_{i^{\prime }j}^{\mathrm{T}}|z_j^{\mathrm{T}}=k_{i^{\prime }j}^{\mathrm{T}},w_i^{\mathrm{T}},d_j^{\mathrm{T}})=(a_{ij}^{\mathrm{T}}{)}^{d_j^{\mathrm{T}}{w}_i^{\mathrm{T}}}.\text{\hspace{1em}(2)}$$

其中，$a_{ij}^{\mathrm{T}}=\frac{sim(k_{i^{\prime }j}^{\mathrm{T}},k_{i^{\prime }j}^{\mathrm{T}})}{{\sum }_{i^{\prime \prime }=1}^{|K_j^{\mathrm{T}}|}sim(k_{i^{\prime \prime }j}^{\mathrm{T}},k_{i^{\prime }j}^{\mathrm{T}})}$表示$K_j^{\mathrm{T}}$中$k_{i^{\prime }j}^{\mathrm{T}}$的辨别度，用$k_{i^{\prime }j}^{\mathrm{T}}$与候选结果集$K_j^{\mathrm{T}}$之间的归一化相似度计算，$sim(k_{i^{\prime \prime }j}^{\mathrm{T}},k_{i^{\prime }j}^{\mathrm{T}})$表示候选结果$k_{i^{\prime \prime }j}^{\mathrm{T}}$和$k_{i^{\prime }j}^{\mathrm{T}}$之间的原始相似度。例如，在手写识别中，$sim(k_{i^{\prime \prime }j}^{\mathrm{T}},k_{i^{\prime }j}^{\mathrm{T}})$表示两个单词（两个字符序列）的相似度对应它们对应外形的相似度。如果$k_{ij}^{\mathrm{T}}$与未知的真值标签$z_j^{\mathrm{T}}$非常相似，那么很可能由工人给出$k_{ij}^{\mathrm{T}}$作为候选答案，这也意味着$sim(k_{i^{\prime \prime }j}^{\mathrm{T}},k_{i^{\prime }j}^{\mathrm{T}})$应接近1（特别是$sim(k_{ij}^{\mathrm{T}},k_{ij}^{\mathrm{T}})=1$）。

其次，如果工人$i$给出的答案与正确答案$k_{i^{\prime }j}^{\mathrm{T}}$不同，即$o_{ij}^{\mathrm{T}}=k_{i^{\prime \prime }j}^{\mathrm{T}}\ne k_{i^{\prime }j}^{\mathrm{T}}$，那么候选回答$k_{i^{\prime \prime }j}^{\mathrm{T}}\in K_j^{\mathrm{T}}$被工人$i$错误地确定为是正确答案的概率是：

$$P(o_{ij}^{\mathrm{T}}=k_{i^{\prime \prime }j}^{\mathrm{T}}|z_j^{\mathrm{T}}=k_{i^{\prime }j}^{\mathrm{T}},w_i^{\mathrm{T}},d_j^{\mathrm{T}})=(1-(a_{ij}^{\mathrm{T}}{)}^{d_j^{\mathrm{T}}{w}_i^{\mathrm{T}}})\theta (k_{i^{\prime \prime }j}^{\mathrm{T}},k_{i^{\prime }j}^{\mathrm{T}}).\text{\hspace{1em}(3)}$$

其中，$\theta (k_{i^{\prime \prime }j}^{\mathrm{T}},k_{i^{\prime }j}^{\mathrm{T}})=\frac{sim(k_{i^{\prime \prime }j}^{\mathrm{T}},k_{i^{\prime }j}^{\mathrm{T}})}{{\sum }_{i=1}^{|K_j^{\mathrm{T}}|}sim(k_{i^{\prime }j}^{\mathrm{T}},k_{ij}^{\mathrm{T}})-1}$表示两个错误结果$k_{i^{\prime \prime }j}^{\mathrm{T}}$和$k_{i^{\prime }j}^{\mathrm{T}}$与所有错误结果的归一化距离比。这有助于更好地捕捉工人的表现，这与现有的模型（如GLAD模型[46]和Dawid-Skene模型[9]）有着明显的区别。

为了化简的公式(2)和(3)，我们定义$\sigma (o_{ij}^{\mathrm{T}})=(a_{ij}^{\mathrm{T}}{)}^{d_j^{\mathrm{T}}{w}_i^{\mathrm{T}}}$和$\delta (o_{ij}^{\mathrm{T}},z_j^{\mathrm{T}})$表示克罗内克函数（Kronecker Delta Function）[37]，进一步简化为$\delta$。然后我们有了

$$P(o_{ij}^{\mathrm{T}}|z_j^{\mathrm{T}},w_i^{\mathrm{T}},d_j^{\mathrm{T}})=\sigma (o_{ij}^{\mathrm{T}}{)}^{\delta }((1-\sigma (o_{ij}^{\mathrm{T}}))\theta (o_{ij}^{\mathrm{T}}){)}^{1-\delta }.\text{\hspace{1em}(4)}$$

在众包中，从已知的先验分布中抽取真值标签$z_j^{\mathrm{T}}$、工人精度参数$w_i^{\mathrm{T}}$和子任务难度$d_j^{\mathrm{T}}$。如果给定了$O_{\ast j}^{\mathrm{T}}$，则可由$O_{\ast j}^{\mathrm{T}}$求出$K_j^{\mathrm{T}}$，我们可用公式(4)通过一些推理方法推理出$z_j^{\mathrm{T}}$在$K_j^{\mathrm{T}}$中的最可能值。

4.2 贝叶斯推理（Bayes-Inf）:不捕获上下文关联

本小节给出了不考虑上下文关联的结果推理的$\mathrm{B}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{s}-\mathrm{I}\mathrm{n}\mathrm{f}$。在定义4的基础上，将替代答案之间的相似度引入到结果推理中，并给出$\mathrm{B}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{s}-\mathrm{I}\mathrm{n}\mathrm{f}$来推理真值标签。最后，我们使用MLE算法和EM算法来估计$\mathrm{B}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{s}-\mathrm{I}\mathrm{n}\mathrm{f}$的参数，并按照[46]中使用的方法来描述EM算法的过程。

4.2.1 Bayes-Inf概述

我们从$\mathrm{C}\mathrm{S}\mathrm{T}$中的子任务$j$的推理模型开始，然后将所有子任务的结果作为$\mathrm{C}\mathrm{S}\mathrm{T}$的最终结果合并到$\mathrm{C}\mathrm{O}\mathrm{V}$中。

对于$\mathrm{C}\mathrm{S}\mathrm{T}$的每个子任务$j$（无真值标签），给出观测数据$O_{\ast j}^{\mathrm{T}}$，并生成候选结果集$K_j^{\mathrm{T}}$。完成子任务$j$的所有工人的准确度参数表示为 W j T = { w i T ∣ w i T W_j^\mathrm{T}=\{w_i^\mathrm{T}|w_i^\mathrm{T} WjT​={wiT​∣wiT​表示回答子任务$j$的工人$i$的准确度$\}$，回答$\mathrm{C}\mathrm{S}\mathrm{T}$的所有工人的准确度参数表示为 W T = { W j T ∣ 0 ≤ j ≤ m } W^\mathrm{T}=\{ W_j^\mathrm{T}|0\leq j\leq m\} WT={WjT​∣0≤j≤m}。然后，子任务$j$的最佳结果如下：

$$k_{i_{j}j}^{\mathrm{T}}={\arg \max }_{k_{i^{\prime }j}^{\mathrm{T}}\in K_j^{\mathrm{T}}}P(z_j^{\mathrm{T}}=k_{i^{\prime }j}^{\mathrm{T}}|O_{\ast j}^{\mathrm{T}},W_j^{\mathrm{T}},d_j^{\mathrm{T}}),\text{\hspace{1em}(5)}$$

其中

$$\begin{array}{rl}P(z_j^{\mathrm{T}}=k_{i^{\prime }j}^{\mathrm{T}}|O_{\ast j}^{\mathrm{T}},W_j^{\mathrm{T}},d_j^{\mathrm{T}})& =\frac{P(z_j^{\mathrm{T}}=k_{i^{\prime }j}^{\mathrm{T}}|W_j^{\mathrm{T}},d_j^{\mathrm{T}})P(O_{\ast j}^{\mathrm{T}}|z_j^{\mathrm{T}}=k_{i^{\prime }j}^{\mathrm{T}},W_j^{\mathrm{T}},d_j^{\mathrm{T}})}{P(O_{\ast j}^{\mathrm{T}}|W_j^{\mathrm{T}},d_j^{\mathrm{T}})}\\ & \propto P(z_j^{\mathrm{T}}=k_{i^{\prime }j}^{\mathrm{T}}|W_j^{\mathrm{T}},d_j^{\mathrm{T}})P(O_{\ast j}^{\mathrm{T}}|z_j^{\mathrm{T}}=k_{i^{\prime }j}^{\mathrm{T}},W_j^{\mathrm{T}},d_j^{\mathrm{T}})\\ & \propto P(z_j^{\mathrm{T}}=k_{i^{\prime }j}^{\mathrm{T}})\prod _{i=1,o_{ij}^{\mathrm{T}}\ne \varphi }^{n}P(o_{ij}^{\mathrm{T}}|z_j^{\mathrm{T}}=k_{i^{\prime }j}^{\mathrm{T}},w_i^{\mathrm{T}},d_j^{\mathrm{T}}).\end{array}\text{\hspace{1em}(6)}$$

注意$p(z_j^{\mathrm{T}})=p(z_j^{\mathrm{T}}=k_{i^{\prime }j}^{\mathrm{T}}|W_j^{\mathrm{T}},d_j^{\mathrm{T}})$是根据我们的图形模型中的条件独立性假设得出的。由于从候选答案中选择正确答案的概率是相同的，所以我们得到$p(z_j^{\mathrm{T}})=1/|K_j^{\mathrm{T}}|$。

利用公式(5)，我们得到每个子任务j的$k_{i_{j}j}^{\mathrm{T}}$。不考虑输出矩阵中的上下文关联，我们可以生成一个$\mathrm{C}\mathrm{O}\mathrm{V}{\mathrm{C}}_{\mathrm{T}}^{\prime }=⟨k_{i_{1}1}^{\mathrm{T}},...k_{i_{j}j}^{\mathrm{T}},...,k_{i_{m}m}^{\mathrm{T}}⟩$，这是定义3中$\mathrm{C}\mathrm{S}\mathrm{T}$的最佳$\mathrm{C}\mathrm{O}\mathrm{V}$。

4.2.2 参数学习

$\mathrm{B}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{s}-\mathrm{I}\mathrm{n}\mathrm{f}$模型的过程包含两个参数集，即工作能力集$W$和任务难度集$D$。每个工人的能力不因任务的不同而不同。因此，我们根据黄金任务的结果使用MLE方法来评估每个工人的能力。因为任务的难度不同。使用基于黄金任务的方法无法获得任务（黄金任务除外）的难度级别。因此，我们使用EM算法来估计没有真值标签的$\mathrm{C}\mathrm{S}\mathrm{T}$的难度，并推理出最终结果，类似于[46]。

(1). 黄金测试任务参数学习

对于一组测试任务 Γ = { ( T ′ , Z T ′ ) } \Gamma=\{(\mathrm{T'},Z^{\mathrm{T'}})\} Γ={(T′,ZT′)}，$O^{{\mathrm{T}}^{\prime }}$是测试任务${\mathrm{T}}^{\prime }$的输出矩阵，$W^{{\mathrm{T}}^{\prime }}$表示完成${\mathrm{T}}^{\prime }$的工人对应的准确度参数，$Z^{{\mathrm{T}}^{\prime }}$是真值标签。未观察到的变量是不同的工人准确度 W T ′ = { w i T ′ } W^\mathrm{T'}=\{w_i^\mathrm{T'}\} WT′={wiT′​}和子任务难度参数 D T ′ = { d j T ′ } D^\mathrm{T'}=\{d_j^\mathrm{T'}\} DT′={djT′​}。对于每个测试任务${\mathrm{T}}^{\prime }$，我们将似然函数$l_{{\mathrm{T}}^{\prime }}$介绍如下：

$$l_{{\mathrm{T}}^{\prime }}(W^{{\mathrm{T}}^{\prime }},D^{{\mathrm{T}}^{\prime }})=\prod _{ij}P(o_{ij}^{{\mathrm{T}}^{\prime }}|z_j^{{\mathrm{T}}^{\prime }},w_i^{{\mathrm{T}}^{\prime }},d_j^{{\mathrm{T}}^{\prime }}).\text{\hspace{1em}(7)}$$

在实践中，我们经常使用多个测试任务作为黄金测试。根据公式(7)，我们得到对数似然函数

$$L_{\Gamma }(W^{{\mathrm{T}}^{\prime }},D^{{\mathrm{T}}^{\prime }})=\ln \prod _{{\mathrm{T}}^{\prime }\in \Gamma }{l}_{{\mathrm{T}}^{\prime }}(W^{{\mathrm{T}}^{\prime }},D^{{\mathrm{T}}^{\prime }}).\text{\hspace{1em}(8)}$$

为了使$L_{\Gamma }(W^{{\mathrm{T}}^{\prime }},D^{{\mathrm{T}}^{\prime }})$最大化，我们可以对函数$L_{\Gamma }$进行区分，得到梯度：

$$\frac{\partial L_{\Gamma }}{\partial w_i^{{\mathrm{T}}^{\prime }}}=\sum _{{\mathrm{T}}^{\prime }\in \Gamma }\sum _j\frac{\delta (o_{ij}^{{\mathrm{T}}^{\prime }},z_j^{{\mathrm{T}}^{\prime }})-\sigma (o_{ij}^{{\mathrm{T}}^{\prime }})}{1-\sigma (o_{ij}^{{\mathrm{T}}^{\prime }})}{d}_j^{{\mathrm{T}}^{\prime }}\ln a_{ij}^{{\mathrm{T}}^{\prime }}.\text{\hspace{1em}(9)}$$

和

$$\frac{\partial L_{\Gamma }}{\partial d_j^{{\mathrm{T}}^{\prime }}}=\sum _i\frac{\delta (o_{ij}^{{\mathrm{T}}^{\prime }},z_j^{{\mathrm{T}}^{\prime }})-\sigma (o_{ij}^{{\mathrm{T}}^{\prime }})}{1-\sigma (o_{ij}^{{\mathrm{T}}^{\prime }})}{w}_i^{{\mathrm{T}}^{\prime }}\ln a_{ij}^{{\mathrm{T}}^{\prime }}.\text{\hspace{1em}(10)}$$

其中符号$\sigma$、$\delta$和$a_{ij}^{{\mathrm{T}}^{\prime }}$在第4.1节中进行了讨论。用公式(9)和(10)，我们可以使用梯度上升法[46]获得$W^{{\mathrm{T}}^{\prime }}$和$D^{{\mathrm{T}}^{\prime }}$。

(2). 用EM算法进行推理

本部分介绍了学习子任务难度参数的EM算法。与黄金测试的情况不同，很难获得工人的真实准确度，即$W^{\mathrm{T}}$未知。对于$\mathrm{C}\mathrm{S}\mathrm{T}\mathrm{T}\in \mathcal{T}$，让$O^{\mathrm{T}}$表示$\mathrm{T}$的输出矩阵，$W^{\mathrm{T}}$表示准确度参数集， D T = { d j ∣ 0 ≤ j ≤ m } D^\mathrm{T}=\{d_j|0\leq j\leq m\} DT={dj​∣0≤j≤m}为$\mathrm{C}\mathrm{S}\mathrm{T}$的难度。由于在加工不同的$\mathrm{C}\mathrm{S}\mathrm{T}$时，工人的准确度参数可以被视为常数，因此我们可以用$W^{{\mathrm{T}}^{\prime }}$来估计$W^{\mathrm{T}}$，即$W^{\mathrm{T}}=W^{{\mathrm{T}}^{\prime }}$。由于$\mathrm{C}\mathrm{S}\mathrm{T}$的不同子任务具有不同的难度参数，因此$\mathrm{T}$的$D^{\mathrm{T}}$仍然未知，我们研究如何学习这些参数。

观测数据$O_{\ast j}^{\mathrm{T}}$是输出矩阵$O^{\mathrm{T}}$的每个子任务样本。未观察到的变量是真值标签$z_j^{\mathrm{T}}$和子任务的难度参数$d_j^{\mathrm{T}}$。$\mathrm{B}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{s}-\mathrm{I}\mathrm{n}\mathrm{f}$的目的是利用观测数据$O_{\ast j}^{\mathrm{T}}$和$w_i^{\mathrm{T}}\in W$有效地搜索不可观测变量 Z T = { z j T } Z^\mathrm{T}=\{z_j^\mathrm{T}\} ZT={zjT​}和$d_j^{\mathrm{T}}$的最可能值。在这里，我们使用期望最大化算法（EM）来获得参数的最大似然估计。

E-步骤： 让$K_j^{\mathrm{T}}$表示具有$m$个子任务的$\mathrm{C}\mathrm{S}\mathrm{T}\mathrm{T}$子任务$j$的候选结果集，$z_j^{\mathrm{T}}$被视为潜在变量。参加$\mathrm{C}\mathrm{S}\mathrm{T}$的工人不能总是完成$\mathrm{C}\mathrm{S}\mathrm{T}$的所有子任务，那么$|O_{\ast j}^{\mathrm{T}}|\le n$。利用最后一个M-步骤计算的$d_j^{\mathrm{T}}$，观察到的输出$O_{\ast j}^{\mathrm{T}}$和$W^{\mathrm{T}}=W^{{\mathrm{T}}^{\prime }}$，候选结果$k_{i^{\prime }j}^{\mathrm{T}}$是子任务$j$正确答案的后验概率可计算如下：

$$P^{k_{i^{\prime }j}^{\mathrm{T}}}=P(z_j^{\mathrm{T}}=k_{i^{\prime }j}^{\mathrm{T}}|O_{\ast j}^{\mathrm{T}},W_j^{\mathrm{T}},d_j^{\mathrm{T}}),\text{\hspace{1em}(11)}$$

其中$P(z_j^{\mathrm{T}}=k_{i^{\prime }j}^{\mathrm{T}}|O_{\ast j}^{\mathrm{T}},W_j^{\mathrm{T}},d_j^{\mathrm{T}})$可以由公式(6)获得。

M-步骤： 最大化辅助函数$Q$，即观测数据和未观测数据 Z T = { z j T } Z^\mathrm{T}=\{z_j^\mathrm{T}\} ZT={zjT​}的联合对数似然期望值，可从$D_{old}^{\mathrm{T}}$参数中获得。根据E-步骤计算的$Z^{\mathrm{T}}$的后验概率，我们定义了辅助函数$Q$：

$$\begin{array}{rl}Q(D^{\mathrm{T}},D_{old}^{\mathrm{T}})& =E(\ln (P(O^{\mathrm{T}},Z^{\mathrm{T}}|W^{{\mathrm{T}}^{\prime }},D_{old}^{\mathrm{T}})))\\ & =E(\ln (\prod _j(P(z_j^{\mathrm{T}})\prod _{i}P(o_{ij}^{\mathrm{T}}|z_j^{\mathrm{T}},w_i^{\mathrm{T}},d_j^{\mathrm{T}})))\\ & =\sum _j\sum _{i^{\prime }=1}^{|K_j^{\mathrm{T}}|}{P}^{k_{i^{\prime }j}^{\mathrm{T}}}\ln P(z_j^{\mathrm{T}}=k_{i^{\prime }j}^{\mathrm{T}})+\sum _{i,j}\sum _{i^{\prime }=1}^{|K_j^{\mathrm{T}}|}{P}^{k_{i^{\prime }j}^{\mathrm{T}}}\ln P(o_{ij}^{\mathrm{T}}|z_j^{\mathrm{T}}=k_{i^{\prime }j}^{\mathrm{T}},w_i^{\mathrm{T}},d_j^{\mathrm{T}}),\end{array}\text{\hspace{1em}(12)}$$

其中$p^{k_{i^{\prime }j}^{\mathrm{T}}}$和$k_{i^{\prime }j}^{\mathrm{T}}$可以用E-步骤中已经估计的$D_{old}^{\mathrm{T}}$得到。

为了最大化$Q(D^{\mathrm{T}},D_{old}^{\mathrm{T}})$，我们可以区分$Q$来获得梯度：

$$\frac{\partial Q}{\partial d_j^{\mathrm{T}}}=\sum _i\sum _{i^{\prime }=1}^{|K_j^{\mathrm{T}}|}{P}^{k_{i^{\prime }j}^{\mathrm{T}}}\frac{\delta (o_{ij}^{\mathrm{T}},k_{i^{\prime }j}^{\mathrm{T}})-\sigma (o_{ij}^{\mathrm{T}})}{1-\sigma (o_{ij}^{\mathrm{T}})}{w}_i^{\mathrm{T}}\ln a_{ij}^{\mathrm{T}},\text{\hspace{1em}(13)}$$

其中，符号$\sigma$、$\delta$和$a_{ij}^{\mathrm{T}}$在第4.1节中进行了讨论。与[46]相似，我们使用$D_{old}^{\mathrm{T}}$通过梯度上升更新新的$D^{\mathrm{T}}$，在当前步骤中局部最大化$Q$。然后，我们迭代地应用E-步骤和M-步骤来获得$D^{\mathrm{T}}$，并使似然最大化。

4.3 Context-Inf（上下文推理）：捕获上下文关联

本小节介绍一个上下文感知推理模型$\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$，它用HMM模型对子任务之间的上下文关联进行建模。接下来，我们给出我们的推理模型来估计参数，其过程也类似于[46]。

4.3.1 CST中的上下文关联

在本小节中，我们给出了两个子任务的候选结果之间上下文关联的定义。例如，对于手写识别，上下文关联可以通过2-gram语言模型获得。我们构造了一个上下文图，其中节点是子任务的候选结果，边是每对的上下文关联。图4显示了一个$\mathrm{C}\mathrm{O}\mathrm{V}$的示例，所有$\mathrm{C}\mathrm{O}\mathrm{V}$都显示在表2中。然后，引入$f(k_{i^{\prime }{j}^{\prime }}^{\mathrm{T}}|k_{ij}^{\mathrm{T}})$来量化$k_{ij}^{\mathrm{T}}$和$k_{i^{\prime }{j}^{\prime }}^{\mathrm{T}}$之间的上下文关联：

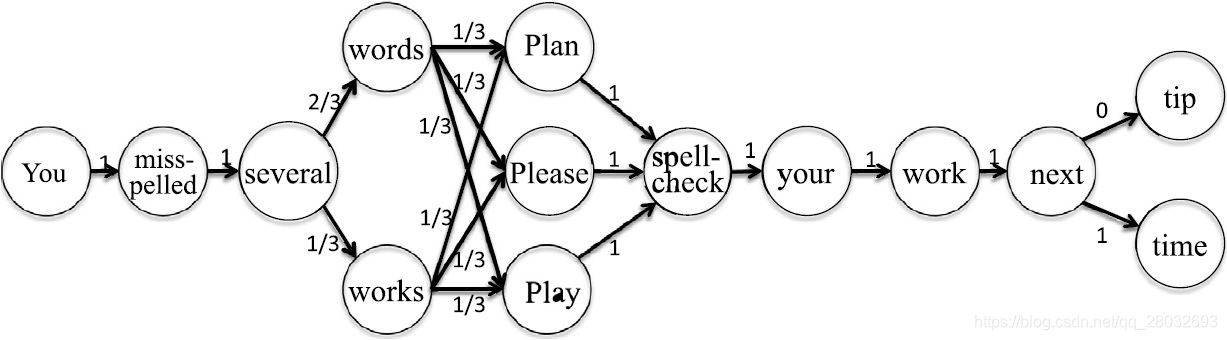
图4. 上下文关联的示例

$$f(k_{i^{\prime }{j}^{\prime }}^{\mathrm{T}}|k_{ij}^{\mathrm{T}})=\frac{weight(k_{ij}^{\mathrm{T}},k_{i^{\prime }{j}^{\prime }}^{\mathrm{T}})}{{\sum }_{l=1}^{n}weight(k_{ij}^{\mathrm{T}},k_{l{j}^{\prime }}^{\mathrm{T}})},\text{\hspace{1em}(14)}$$

其中$j\ne j^{\prime }$，权重$weight(k_{ij}^{\mathrm{T}},k_{i^{\prime }{j}^{\prime }}^{\mathrm{T}})$表示子任务$j$的候选结果$k_{ij}^{\mathrm{T}}$与另一个子任务$j^{\prime }$的$k_{i^{\prime }{j}^{\prime }}^{\mathrm{T}}$之间的上下文关联度，可从外部知识库中获得。例如，我们可以量化手写识别每对子任务的两个候选结果之间的上下文关联，如下所示：

$$f(k_{i^{\prime }{j}^{\prime }}^{\mathrm{T}}|k_{ij}^{\mathrm{T}})=\{\begin{array}{cc}\frac{N(k_{ij}^{\mathrm{T}},k_{i^{\prime }{j}^{\prime }}^{\mathrm{T}})}{{\sum }_{l=0}^{n}N(k_{ij}^{\mathrm{T}},k_{l{j}^{\prime }}^{\mathrm{T}})}& j^{\prime }=j+1\\ 0& j^{\prime }\ne j+1\end{array}.\text{\hspace{1em}(15)}$$

其中$N(k_{ij}^{\mathrm{T}},k_{l{j}^{\prime }}^{\mathrm{T}})$表示两个词在文本语料库中共现的频率，如英国国家语料库、谷歌n-gram语料库。

为了便于在结果推理中使用，我们将输出矩阵的上下文图的邻接矩阵指定为$C^{\mathrm{T}}$，一个表示$\mathrm{C}\mathrm{S}\mathrm{T}$中所有上下文关联的上下文矩阵。

4.3.2 上下文感知推理模型

我们描述上下文信息来推理$\mathrm{C}\mathrm{S}\mathrm{T}$最可能的$\mathrm{C}\mathrm{O}\mathrm{V}$（没有真值标签），考虑上下文关联。

给定候选结果集 { K j T ∣ 0 ≤ j ≤ m } \{ K_j^\mathrm{T}|0\leq j\leq m\} {KjT​∣0≤j≤m}从工人的输出矩阵$O^{\mathrm{T}}$中获得。$\mathrm{C}\mathrm{S}\mathrm{T}$的上下文矩阵 C T = { f ( k i j T ∣ k i ′ j ′ T ) } C^\mathrm{T}=\{f(k_{ij}^\mathrm{T}|k_{i'j'}^\mathrm{T})\} CT={f(kijT​∣ki′j′T​)}可由公式(14)计算。子任务的推理结果取决于三个因素：难度、工人的准确度和每对答案之间的上下文相关性。我们使用图5所示的隐马尔可夫模型[15] $\lambda =(\mathcal{A},\mathcal{B},\pi )$来捕获$\mathrm{T}$子任务之间的上下文相关性，并将每个$k_{ij}^{\mathrm{T}}$作为HMM的隐态； π T = { π i T = E ( z 1 T = k i 1 T ) } \pi^\mathrm{T}=\{ \pi_i^\mathrm{T}= E(z_1^\mathrm{T}=k_{i1}^\mathrm{T})\} πT={πiT​=E(z1T​=ki1T​)}是$k_{i1}^{\mathrm{T}}$作为$\mathrm{C}\mathrm{S}\mathrm{T}\mathrm{T}$中第一个子任务的答案的先验概率；${\mathcal{A}}^{\mathrm{T}}=C^{\mathrm{T}}$是HMM的状态转换概率矩阵； B T = { b k i j T ( O ∗ j T ) } \mathcal{B}^\mathrm{T}=\{ b_{k_{ij}^\mathrm{T}}(O_{*j}^\mathrm{T})\} BT={bkijT​​(O∗jT​)}是HMM的输出概率矩阵，$b_{k_{ij}^{\mathrm{T}}}(O_{\ast j}^{\mathrm{T}})$描述观测$O_{\ast j}^{\mathrm{T}}$与隐态$k_{ij}^{\mathrm{T}}$之间的关系，定义如下：

$$\begin{array}{rl}{b}_{k_{ij}^{\mathrm{T}}}(O_{\ast j}^{\mathrm{T}})& =P(O_{\ast j}^{\mathrm{T}}|z_j^{\mathrm{T}}=k_{ij}^{\mathrm{T}},W_j^{\mathrm{T}},d_j^{\mathrm{T}})\\ & =\frac{P(W_j^{\mathrm{T}},O_{\ast j}^{\mathrm{T}}|z_j^{\mathrm{T}}=k_{ij}^{\mathrm{T}},d_j^{\mathrm{T}})}{P(W_j^{\mathrm{T}}|z_j^{\mathrm{T}}=k_{ij}^{\mathrm{T}},d_j^{\mathrm{T}})}\\ & =\frac{P(W_j^{\mathrm{T}}|O_{\ast j}^{\mathrm{T}},z_j^{\mathrm{T}}=k_{ij}^{\mathrm{T}},d_j^{\mathrm{T}})P(O_{\ast j}^{\mathrm{T}}|z_j^{\mathrm{T}}=k_{ij}^{\mathrm{T}},d_j^{\mathrm{T}})}{P(W_j^{\mathrm{T}}|z_j^{\mathrm{T}}=k_{ij}^{\mathrm{T}},d_j^{\mathrm{T}})}\\ & =\frac{{\prod }_{w_{i^{\prime }}\in W_j^{\mathrm{T}}}P(w_{i^{\prime }}^{\mathrm{T}}|O_{\ast j}^{\mathrm{T}},z_j^{\mathrm{T}}=k_{ij}^{\mathrm{T}},d_j^{\mathrm{T}}){\prod }_{w_{i^{\prime }}\in W_j^{\mathrm{T}}}P(o_{ij}^{\mathrm{T}}|z_j^{\mathrm{T}}=k_{ij}^{\mathrm{T}},d_j^{\mathrm{T}})}{{\prod }_{w_{i^{\prime }}\in W_j^{\mathrm{T}}}P(w_{i^{\prime }}^{\mathrm{T}}|z_j^{\mathrm{T}}=k_{ij}^{\mathrm{T}},d_j^{\mathrm{T}})}\\ & =\prod _{w_{i^{\prime }}\in W_j^{\mathrm{T}}}P(o_{i^{\prime }j}^{\mathrm{T}}|z_j^{\mathrm{T}}=k_{ij}^{\mathrm{T}},w_{i^{\prime }}^{\mathrm{T}},d_j^{\mathrm{T}}).\end{array}\text{\hspace{1em}(16)}$$

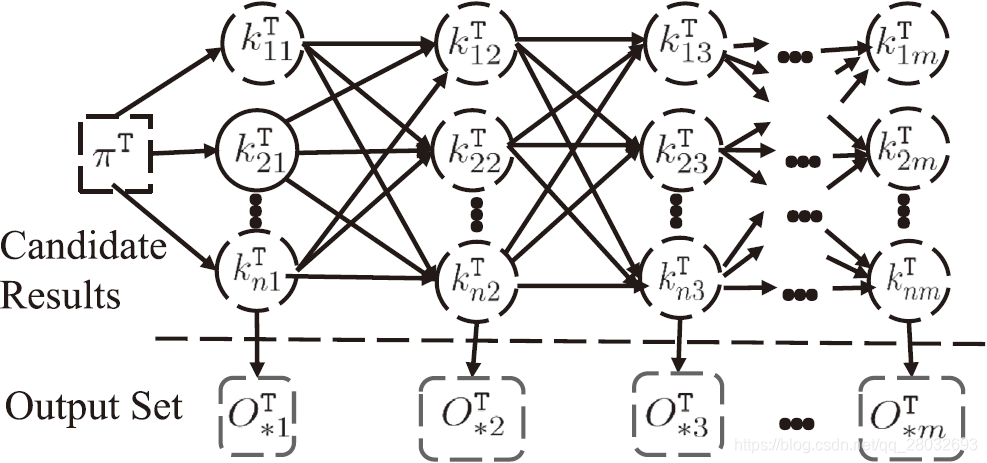
图5. HMM用于结果推理

这里，如$P(W_j^{\mathrm{T}}|O_{\ast j}^{\mathrm{T}},z_j^{\mathrm{T}}=k_{ij}^{\mathrm{T}},d_j^{\mathrm{T}})P(O_{\ast j}^{\mathrm{T}}|z_j^{\mathrm{T}}=k_{ij}^{\mathrm{T}},d_j^{\mathrm{T}})=P(W_j^{\mathrm{T}},O_{\ast j}^{\mathrm{T}}|z_j^{\mathrm{T}}=k_{ij}^{\mathrm{T}},d_j^{\mathrm{T}})$，第三步可以从第二步推理出来。由于在上下文信息中假定工人彼此独立，第四步可以直接获得。

为了简单起见，我们假设子任务的候选输出遵循$K_j^{\mathrm{T}}$中的统一分布，即$p(z_j^{\mathrm{T}})=\frac{1}{|K_j^{\mathrm{T}}|}$。注意，候选输出的其他分布也可以同样应用。

对于没有真值标签的$\mathrm{C}\mathrm{S}\mathrm{T}$，可以用公式(14)计算状态转移矩阵$\mathcal{A}$，用公式(16)给出输出概率，并设置两个参数$D^{\mathrm{T}}$和$W^{\mathrm{T}}$，从而将$\mathrm{I}\mathrm{C}\mathrm{O}\mathrm{V}$问题转化为在隐马尔可夫模型${\lambda }^{\mathrm{T}}$中搜索最可能的隐态序列的问题。换句话说，给定$O$和$\lambda$，目标是找到解释$O$的最佳状态序列$\mathrm{C}\mathrm{O}\mathrm{V}$，其目的是使$P(c_{\mathrm{T}}|{\lambda }^{\mathrm{T}},O^{\mathrm{T}})$最大化。这是与HMM相关的基本问题之一[35]。因此，我们有：

$$\begin{array}{rl}{c}_{\mathrm{T}}^{\prime }& ={\arg \max }_{c_{\mathrm{T}}\in {\mathcal{C}}^{\mathrm{T}}}P(c_{\mathrm{T}}|{\lambda }^{\mathrm{T}},O^{\mathrm{T}})\\ & ={\arg \max }_{c_{\mathrm{T}}\in {\mathcal{C}}^{\mathrm{T}}}\frac{P(O^{\mathrm{T}},c_{\mathrm{T}}|{\lambda }^{\mathrm{T}})}{P(O^{\mathrm{T}}|{\lambda }^{\mathrm{T}})}\\ & ={\arg \max }_{c_{\mathrm{T}}\in {\mathcal{C}}^{\mathrm{T}}}\frac{P(O^{\mathrm{T}},c_{\mathrm{T}}|{\lambda }^{\mathrm{T}})}{{\sum }_{c_{\mathrm{T}}\in C}P(O^{\mathrm{T}},c_{\mathrm{T}}|{\lambda }^{\mathrm{T}})}\\ & ={\arg \max }_{c_{\mathrm{T}}\in {\mathcal{C}}^{\mathrm{T}}}P(O^{\mathrm{T}},c_{\mathrm{T}}|{\lambda }^{\mathrm{T}})\\ & ={\arg \max }_{c_{\mathrm{T}}\in {\mathcal{C}}^{\mathrm{T}}}{\pi }_{o_{i1}^{\mathrm{T}}}\prod _{k_{ij}^{\mathrm{T}}\in c_{\mathrm{T}}}{b}_{k_{ij}^{\mathrm{T}}}(O_{\ast j}^{\mathrm{T}})f(k_{ij+1}^{\mathrm{T}}|k_{ij}^{\mathrm{T}}).\end{array}\text{\hspace{1em}(17)}$$

如果提供了参数集$D^{\mathrm{T}}$和$W^{\mathrm{T}}$，我们可以用维特比算法（Viterbi Algorithm）[5,36]计算$c_{\mathrm{T}}^{\prime }$来确定HMM的最可能隐藏状态序列。但是，${\lambda }^{\mathrm{T}}$有两个未知的参数集$W^{\mathrm{T}}$和$D^{\mathrm{T}}$，我们将在下一小节中描述如何学习参数。

4.3.3 参数学习

在本节中，我们讨论了$\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$的参数学习（即$\mathrm{C}\mathrm{S}\mathrm{T}$的HMM模型），目的是找到${\lambda }^{\prime }={\arg \max }_{\lambda }p(O|{\lambda }^{\prime })$。这里${\lambda }^{\mathrm{T}}=({\mathcal{A}}^{\mathrm{T}},{\mathcal{B}}^{\mathrm{T}},{\pi }^{\mathrm{T}})$。从外部知识库中直接得到$({\mathcal{A}}^{\mathrm{T}}$，通过计算工人的答案得到${\pi }^{\mathrm{T}}$，用$b_{k_{ij}^{\mathrm{T}}}(O_{\ast j}^{\mathrm{T}})$得到$\mathcal{B}$，$b_{k_{ij}^{\mathrm{T}}}(O_{\ast j}^{\mathrm{T}})$包含两个参数集$(D,W)$。对于参数集$W$，我们将使用最大似然估计和黄金测试任务。参数集$D$可以通过使用EM来学习HMM[36]的参数，这类似于我们前面提到的$\mathrm{B}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{s}-\mathrm{I}\mathrm{n}\mathrm{f}$中的参数学习和文献[46]中的EM算法。

(1). 黄金测试任务参数学习

本小节介绍了如何使用黄金测试的最大似然估计（MLE）算法估计准确度参数$W$。

对于测试任务${\mathrm{T}}^{\prime }$，上下文矩阵$C^{{\mathrm{T}}^{\prime }}$、真值标签$Z^{{\mathrm{T}}^{\prime }}$和观测变量$O_{\ast j}^{{\mathrm{T}}^{\prime }}$都是已知的。与4.3.2节类似，我们使用隐马尔可夫模型${\lambda }^{{\mathrm{T}}^{\prime }}=({\mathcal{A}}^{{\mathrm{T}}^{\prime }},{\mathcal{B}}^{{\mathrm{T}}^{\prime }},{\pi }^{{\mathrm{T}}^{\prime }})$来捕获测试任务$\mathrm{T}$子任务之间的上下文相关性，其中HMM ${\lambda }^{{\mathrm{T}}^{\prime }}$的最可能隐藏状态序列是$Z^{\mathrm{T}}$，${\mathcal{A}}^{{\mathrm{T}}^{\prime }}=C^{\mathrm{T}}$和${\mathcal{B}}^{{\mathrm{T}}^{\prime }}=b_{z_j^{{\mathrm{T}}^{\prime }}}(O_{\ast j}^{{\mathrm{T}}^{\prime }})$，其中$b_{z_j^{{\mathrm{T}}^{\prime }}}(O_{\ast j}^{{\mathrm{T}}^{\prime }})$由公式(16)定义，有两个未知参数集$W^{{\mathrm{T}}^{\prime }}$和$D^{{\mathrm{T}}^{\prime }}$。为了学习参数$W^{{\mathrm{T}}^{\prime }}$,$D^{{\mathrm{T}}^{\prime }}$，我们给出了测试任务${\mathrm{T}}^{\prime }$的似然函数$l_{{\mathrm{T}}^{\prime }}$：

$$\begin{array}{rl}{l}_{{\mathrm{T}}^{\prime }}(W^{{\mathrm{T}}^{\prime }},D^{{\mathrm{T}}^{\prime }})& =\ln P(C^{{\mathrm{T}}^{\prime }},Z^{{\mathrm{T}}^{\prime }}|{\lambda }^{{\mathrm{T}}^{\prime }})\\ & =\ln ({\pi }_{z_1}^{{\mathrm{T}}^{\prime }}\prod _{j=1}^{m}f(z_{j+1}^{{\mathrm{T}}^{\prime }}|z_j^{{\mathrm{T}}^{\prime }})b_{z_j^{{\mathrm{T}}^{\prime }}}(O_{\ast j}^{{\mathrm{T}}^{\prime }}))\\ & =\ln {\pi }_{z_1}^{{\mathrm{T}}^{\prime }}+\sum _{j=1}^m\ln f(z_{j+1}^{{\mathrm{T}}^{\prime }}|z_j^{{\mathrm{T}}^{\prime }})+\sum _{j=1}^m\ln b_{z_j^{{\mathrm{T}}^{\prime }}}(O_{\ast j}^{{\mathrm{T}}^{\prime }}).\end{array}\text{\hspace{1em}(18)}$$

利用公式(18)，我们希望最大化$l_{{\mathrm{T}}^{\prime }}$。因为第一项和第二项是常数，所以似然函数$l_{{\mathrm{T}}^{\prime }}$的最大值取决于第三项。第三项与输出函数$b_{z_j^{{\mathrm{T}}^{\prime }}}(O_{\ast j}^{{\mathrm{T}}^{\prime }})$相关，独立于黄金测试任务中的子任务。因此，输出函数的参数学习与$\mathrm{B}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{s}-\mathrm{I}\mathrm{n}\mathrm{f}$的参数学习是相同的。

(2). 用EM算法进行推理

对于没有真值标签的$\mathrm{C}\mathrm{S}\mathrm{T}$，类似于$\mathrm{B}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{s}-\mathrm{I}\mathrm{n}\mathrm{f}$，我们可以通过测试任务得到参数值$W^{\mathrm{T}}=W^{{\mathrm{T}}^{\prime }}$。$\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$包含一个需要学习的参数集 D T = { d j T } D^\mathrm{T}=\{d_j^\mathrm{T}\} DT={djT​}。

在HMM[5]的学习过程之前，我们首先回顾了前面的过程。我们定义

$${\alpha }_j(k_{ij})=P(O_{\ast 1},...,O_{\ast j},k_{ij}|\lambda ),$$

这是看到部分序列$O_{\ast 1},...,O_{\ast j}$的概率，在时间$j$处结束于状态$i$。我们可以有效地将${\alpha }_i(t)$递归定义为：

• ${\alpha }_j(k_{i1})={\pi }_i^{\mathrm{T}}{b}_{k_{ij}^{\mathrm{T}}}(O_{\ast j}^{\mathrm{T}})$
• ${\alpha }_j(k_{ij}^{\mathrm{T}})=[{\sum }_{i^{\prime }=1}^{|K_{j-1}^{\mathrm{T}}|}{\alpha }_j(f(k_{ij}^{\mathrm{T}}|k_{i^{\prime }j-1}^{\mathrm{T}}))]b_{k_{ij}^{\mathrm{T}}}(O_{\ast i}^{\mathrm{T}})$
• $P(O|\lambda )={\sum }_{j=1}^N{\alpha }_j(T)$

反向过程类似：${\beta }_j(t)=P(O_{\ast t+1},...,O_{\ast T}|k_{it},\lambda )$，这是看到部分序列$O_{\ast t+1},...,O_{\ast T}$的概率，并在时间$t$从状态$i$开始。我们可以有效地将${\beta }_j(t)$递归定义为：

• ${\beta }_j(k_{i1})=1$
• ${\beta }_j(k_{ij}^{\mathrm{T}})={\sum }_{i^{\prime }=1}^{|K_{j+1}^{\mathrm{T}}|}f(k_{i^{\prime }j+1}^{\mathrm{T}}|k_{ij}^{\mathrm{T}}){\beta }_{ij}(k_{i^{\prime }j+1}^{\mathrm{T}})b_{k_{ij}^{\mathrm{T}}}(O_{\ast j}^{\mathrm{T}})$
• $P(O|\lambda )={\sum }_{j=1}^N{\beta }_j(1){\pi }_i{b}_j(O_{\ast 1})$

基于HMM中描述的马尔可夫性质的条件独立性，我们将概率$p^{k_{ij}^{\mathrm{T}}}$定义为：

$$\begin{array}{rl}{P}^{k_{ij}^{\mathrm{T}}}& =P(O^{\mathrm{T}},k_{ij}^{\mathrm{T}}|{\lambda }^{\mathrm{T}})\\ & =P(O_{\ast 1},...,O_{\ast j},k_{ij}^{\mathrm{T}}|{\lambda }^{\mathrm{T}})P(O_{\ast j+1},...,O_{\ast m}|k_{ij}^{\mathrm{T}},{\lambda }^{\mathrm{T}})\\ & ={\alpha }_j(k_{ij}^{\mathrm{T}}){\beta }_j(k_{ij}^{\mathrm{T}}),\end{array}\text{\hspace{1em}(19)}$$

E-步骤： 让$c^{\mathrm{T}}=<k_{i_{1}1}^{\mathrm{T}},...,k_{i_{j}j}^{\mathrm{T}},...,k_{i_{m}m}^{\mathrm{T}}>$是$\mathrm{C}\mathrm{S}\mathrm{T}$的$\mathrm{C}\mathrm{O}\mathrm{V}$。$C_{\mathrm{T}}$是$\mathrm{C}\mathrm{S}\mathrm{T}$正确答案的后验概率可以得到：

$$P(O^{\mathrm{T}},c^{\mathrm{T}}|{\lambda }_{old}^{\mathrm{T}})={\pi }_{k_{i_{l}1}^{\mathrm{T}}}\prod _{j=0}^{m}f(k_{i_{j}j}^{\mathrm{T}}|k_{i_{j-1}j-1}^{\mathrm{T}})b_{k_{i_{j}j}^{\mathrm{T}}}(O_{\ast j}^{\mathrm{T}}),\text{\hspace{1em}(20)}$$

M-步骤：
设${\mathcal{C}}^{\mathrm{T}}$为所有可能的$\mathrm{C}\mathrm{O}\mathrm{V}$的集合，对数似然函数$Q$定义如下：

$$\begin{array}{rl}Q({\lambda }^{\mathrm{T}},{\lambda }_{old}^{\mathrm{T}})& =\sum _{c_{\mathrm{T}}\in {\mathcal{C}}^{\mathrm{T}}}\ln P(O^{\mathrm{T}},c_{\mathrm{T}}|{\lambda }^{\mathrm{T}})p(O^{\mathrm{T}},c_{\mathrm{T}}|{\lambda }_{old}^{\mathrm{T}})\\ & \begin{array}{rl}=& \sum _{c_{\mathrm{T}}\in {\mathcal{C}}^{\mathrm{T}}}\ln {\pi }_{k_{i_{1}1}^{\mathrm{T}}}P(O^{\mathrm{T}},c_{\mathrm{T}}|{\lambda }_{old}^{\mathrm{T}})\\ & +\sum _{c_{\mathrm{T}}\in {\mathcal{C}}^{\mathrm{T}}}(\sum _{j=1}^m\ln (f(k_{i_{j}j}^{\mathrm{T}}|k_{i_{j-1}j-1}^{\mathrm{T}})))P(O^{\mathrm{T}},c_{\mathrm{T}}|{\lambda }_{old}^{\mathrm{T}})\\ & +\sum _{c_{\mathrm{T}}\in {\mathcal{C}}^{\mathrm{T}}}(\sum _{j=1}^m\ln (b_{k_{i_{j}j}^{\mathrm{T}}}(O_{\ast j}^{\mathrm{T}})))P(O^{\mathrm{T}},c_{\mathrm{T}}|{\lambda }_{old}^{\mathrm{T}}).\end{array}\end{array}\text{\hspace{1em}(21)}$$

因此，我们可以区分$Q$来得到梯度：

$$\frac{\partial Q}{\partial d_j^{\mathrm{T}}}=\sum _{i_j=0}^{|K_j^{\mathrm{T}}|}{P}^{k_{i_{j}j}^{\mathrm{T}}}\sum _{i=1}^n\frac{\delta (o_{ij}^{\mathrm{T}},k_{i_{j}j}^{\mathrm{T}})-\sigma (k_{i_{j}j}^{\mathrm{T}})}{1-\sigma (k_{i_{j}j}^{\mathrm{T}})}{w}_i^{\mathrm{T}}\ln (a_{i_{j}j}^{\mathrm{T}}),\text{\hspace{1em}(22)}$$

其中$P^{k_{i_{j}j}^{\mathrm{T}}}$是根据最后一个E-步骤估计的参数值${\lambda }^{old}$推理得出的。这里，与$\mathrm{B}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{s}-\mathrm{I}\mathrm{n}\mathrm{f}$类似，我们使用$D_{old}^{\mathrm{T}}\in {\lambda }^{old}$通过梯度上升更新新的$D^{\mathrm{T}}\in \lambda$，从而在当前步骤中局部最大化$Q$。然后采用E-步骤和M-步骤迭代法，通过最大化$Q$来计算$D^{\mathrm{T}}$。

5 POMDP迭代决策

本节研究$\mathrm{I}\mathrm{D}\mathrm{P}$问题以确定是否终止迭代过程。迭代改进方法如图2所示。当前轮次中的工人将被显示上一轮的结果，并要求对其进行改进。这个过程具有马尔可夫的性质。形式上，让$q_c\in [0,1]$和$q_{c+1}\in [0,1]$分别表示$c_{\mathrm{T}}^{\prime }$和$c_{\mathrm{T}}$的质量，我们知道工人有$1-q_{c+1}$选择$c_{\mathrm{T}}^{\prime }$的概率。由于$(q_c,q_{c+1})$只是部分可观测的，而当前迭代的结果只依赖于先前的迭代，因此我们可以将此问题表述为部分可观测的马尔可夫决策问题（Partially Observable Markov Decision Problem，$\mathrm{P}\mathrm{O}\mathrm{M}\mathrm{D}\mathrm{P}$）。

定义5（CST的POMDP）。 $\mathrm{C}\mathrm{S}\mathrm{T}$的$\mathrm{P}\mathrm{O}\mathrm{M}\mathrm{D}\mathrm{P}$是一个六元组$⟨\mathcal{S},\Lambda ,\mathcal{R},\mathcal{T},\mathcal{O},\mathcal{P}⟩$，其中

• S = { ⟨ q c + 1 , q c ⟩ } \mathcal{S}=\{ \langle q_{c+1},q_c\rangle\} S={⟨qc+1​,qc​⟩}是一组有限的离散状态，$q_{c+1}$和$q_c$分别是$c_{\mathrm{T}}^{\prime }$和$c_{\mathrm{T}}$的质量；
• Λ = { \Lambda=\{ Λ={创建新的众包任务，提交推理输出$\}$是动作集；
• $\mathcal{R}={\mathcal{R}}_0+{\mathcal{R}}_S$是奖励函数，${\mathcal{R}}_0$是为工人参与而向其支付的固定金额，${\mathcal{R}}_S$是基于工人贡献质量$q$的动态奖励；
• $\mathcal{T}$：$\mathcal{S}\times \mathcal{O}\times \mathcal{S}\to [0,1]$为转换函数，具体如下：
• O = { c T ′ , c T } \mathcal{O}=\{ c'_\mathrm{T},c_\mathrm{T}\} O={cT′​,cT​}是一组有限的观察结果，$c_{\mathrm{T}}^{\prime }$和$c_{\mathrm{T}}$在我们的$\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$模型中定义；
• $\mathcal{P}$：$\mathcal{S}\times \mathcal{O}\to [0,1]$是观测函数。

转换函数。 当一个新的推理结果生成并且当前状态$(q_c,q_{c+1})$未知时，就会调用问题中的状态转换。$c_{\mathrm{T}}$的质量取决于对所有的工人$(1,2,...,n)$。由于每个工人都是独立的，每个工人都可以改进$\mathrm{C}\mathrm{O}\mathrm{V}$，推理结果遵循条件分布$f(q_{c+1}|q_c,i)$，我们可以计算转换函数，即$f(q_{c+1}|q_c,i_1=1,i_2=2,...,i_n=n)$，

$$f(q_{c+1}|q_c,i_1,i_2,...,i_n)=\sum _{i=1}^n{\gamma }_i\cdot f(q_{c+1}|q_c,i),\text{\hspace{1em}(23)}$$

其中${\gamma }_i$是转换函数混合条件分布的参数，${\sum }_{i=1}^n{\gamma }_i=1$-。我们可以计算${\gamma }_i=\frac{\frac{1}{w_i}}{{\sum }_{i^{\prime }=1}^n\frac{1}{w_{i^{\prime }}}}$，其中$w_i$由EM算法计算（见第4节）。

置信度更新。 在我们的模型中，基于子任务的难度和工人的准确度，可以改变对先前聚合结果质量的置信度。如果输出质量已经很高，而且所有子任务都不容易改进，那么我们应该增加$c_{\mathrm{T}}^{\prime }$的质量估计。同样，如果大多数工人都同意当前的结果$c_{\mathrm{T}}$而不是上一步的结果$c_{\mathrm{T}}^{\prime }$，那么很可能我们可以显著提高$c_{\mathrm{T}}^{\prime }$，并且质量应该反映出这些知识。为了更新其对每个改进步骤质量的了解，$\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$首先使用子任务的质量估计来估计子任务的难度，并且可以给出改进的难度$d_i^c$。对于所有子任务，我们可以给出向量$⟨d_1^c,d_2^c,...,d_m^c⟩$，计算$\mathrm{C}\mathrm{S}\mathrm{T}$的难度如下：

$$d_T^c=\prod _j^m{d}_j^c.\text{\hspace{1em}(24)}$$

观测函数。虽然我们不确定新的聚合结果是否优于旧的结果。我们给出了同样的场景：我们为员工提供$\mathrm{C}\mathrm{S}\mathrm{T}$和候选人答案，并要求员工选择最佳结果。我们根据$\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$评估每个$\mathrm{C}\mathrm{O}\mathrm{V}$的质量。在结果推理中，当前聚合结果的$\mathrm{C}\mathrm{O}\mathrm{V}{c}_{\mathrm{T}}$和先前聚合结果的$\mathrm{C}\mathrm{O}\mathrm{V}{c}_{\mathrm{T}}^{\prime }$的全局评估指标$Pr(c_{\mathrm{T}})=p(O,c_{\mathrm{T}}|\lambda )$，我们可以计算观测函数：

$$Pr(q_{c+1}>q_c|c_{\mathrm{T}},c_{\mathrm{T}}^{\prime })=\frac{Pr(c_{\mathrm{T}})}{Pr(c_{\mathrm{T}}^{\prime })+Pr(c_{\mathrm{T}})}.\text{\hspace{1em}(25)}$$

定义5描述了处理CST的控制模型，我们的目标是获得更好的效用，所以我们定义了效用估计。

效用估计。 然后我们讨论如何估计众包任务的效用。在这一点上，我们已经收到k工人的n个输出。基于我们的$\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$模型，我们可以得到装配结果及其质量$q_c$。设$\Delta (q)=q_c-q_{c-1}$，${\mathcal{R}}_s={\mu }_{\mathcal{S}}(q_c)=\frac{e^{\Delta q}-1}{e-1}$表示当前迭代的效用。如果是$\Delta q=0$，${\mu }_{\mathcal{S}}(\Delta q)=0$；否则是（如果是$\Delta q=1$），${\mu }_{\mathcal{S}}(\Delta q)={\mathcal{R}}_s$，它表示工人在第一次迭代中完全和准确地完成任务的概率。那么我们的效用估计方程如下：

$$\mathcal{V}(\mathcal{S})=-{\mathcal{R}}_0\ast k+{\mu }_{\mathcal{S}}(\Delta q).\text{\hspace{1em}(26)}$$

考虑到当前状态$\mathcal{S}$和下一个状态${\mathcal{S}}^{\prime }$，如果${\mathcal{S}}^{\prime }>\mathcal{S}$，我们转到${\mathcal{S}}^{\prime }$；否则我们保持当前状态$\mathcal{S}$。

利用定义5和效用估计函数（公式(26)），我们可以迭代地利用众包提高CST过程的质量。当成本达到请求者提供的奖励预算，或者随着迭代次数的增加质量不能进一步提高时，迭代过程将终止。注意，与现有方法不同，我们的模型具有较少的状态数，从而降低了决策复杂性。

6 实验评估

我们在两组具有代表性的$\mathrm{C}\mathrm{S}\mathrm{T}$上进行了大量的实际实验，并与最先进的方法进行了比较。在本节中，我们将介绍我们的模型和算法的评估结果。

6.1. 实验评估

在我们的实验中，我们选择了两组任务：手写识别和音频转录。它们都包含了$\mathrm{C}\mathrm{S}\mathrm{T}$的典型特征，其中每个任务都由一组子任务组成，子任务之间的上下文关联对于从人群中获得高质量的结果至关重要。所有的任务都发表在CrowdFlower上。我们将在后面详细描述每一组任务的众包流程。

评估从三个方面进行：

1. 任务分割策略如何影响结果质量；
2. 上下文关联对结果推断的重要性；
3. 迭代众包如何提高结果质量。

对于第二次评估，运行以下四种推理方法进行比较：

• Task-Inf： 这种推理方法是任务导向方法（即多投票）的一种实现，并在文献[40]中提出。
• SAM： 这是我们在[17]中提出的方法，在这里我们考虑了$\mathrm{C}\mathrm{S}\mathrm{T}$的内部结构以及工人在一个子任务中的表现对其他子任务结果推断的影响。我们已经在[17]中证明了SAM优于现有方法[9,40,46]。
• Bayes-Inf： 这是第4.2节中描述的面向子任务方法的实现。
• Context-Inf： 这是第4.2节中描述的面向子任务方法的实现。

我们实现了上述四种方法的相应迭代版本，分别表示为$\mathrm{i}\mathrm{T}\mathrm{a}\mathrm{s}\mathrm{k}-\mathrm{I}\mathrm{n}\mathrm{f}$、$\mathrm{i}\mathrm{S}\mathrm{A}\mathrm{M}$、$\mathrm{i}\mathrm{B}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{s}-\mathrm{I}\mathrm{n}\mathrm{f}$和$\mathrm{i}\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$，并运行它们进行第三次评估。

对于这两组任务，我们使用谷歌n-gram Viewer计算子任务之间的上下文关联。为了简单起见，我们使用2-gram根据等式(15)计算上下文相关。

为了获得$\mathrm{C}\mathrm{S}\mathrm{T}\mathrm{T}$中子任务$j$的两个候选结果的：$k_{ij}^{\mathrm{T}}$和$k_{i^{\prime }j}^{\mathrm{T}}$相似度，我们直接计算了手写识别任务中两个单词（字符串）的外观相似度。对于音频识别任务，我们使用两个单词（字符串）对应的语音符号的外观来计算它们的相似度。最后，我们得到了下面的公式来计算公式(3)中使用的两个候选输出的相似度：

$$sim(k_{ij}^{\mathrm{T}},k_{i^{\prime }j}^{\mathrm{T}})=\frac{{\sum }_{i=1}^N{s}_i}{N}.\text{\hspace{1em}(27)}$$

这里，$N$表示字符串的长度，$s_i$表示两个字符的外观相似性，由OpenCV软件计算。

6.2 手写识别结果

6.2.1 数据集和准备工作

对于手写识别任务，向工人展示两张包含手写文本的图像，并要求他们转录文本。数据集是从IAM数据库[30,31]获取的。我们从500位不同作者提供的1500幅包含手写文本的图片中随机选取30幅。每幅图像有5-11行文本，其中最大包含8个句子。我们将手写文本分成句子，然后总共得到130个句子。我们把每一句话都看作是在CrowdFlower上发表的一项任务。每一页包含10个任务，每个任务的成本为4美分，由5名来自CrowdFlower的3级质量工人处理。完成任务的最后期限设置为1天。

6.2.2 任务分割策略

正如我们所讨论的，很难定义$\mathrm{C}\mathrm{S}\mathrm{T}$的一般任务分割策略。因此，我们通过观察字迹识别任务随任务粒度变化的结果质量，对这一问题进行了实证研究。在本实验中，我们使用五幅图像，每幅包含8个句子，来生成不同粒度的众包任务。我们设计了8个策略，通过改变$\mathrm{C}\mathrm{S}\mathrm{T}$中包含的最大句子数。例如，策略5定义了2个$\mathrm{C}\mathrm{S}\mathrm{T}$：一个有5个句子，另一个有3个句子。对于每个策略，我们将相应的$\mathrm{C}\mathrm{S}\mathrm{T}$发布到CrowdFlower，并使用$\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$进行结果推理。如图6(a)所示，当一个任务中有更多的句子时，平均结果质量从65%下降到近40%，这证实了我们的推测，工作量的增加会影响整体工人的准确性。因此，在下面的实验中，我们将$\mathrm{C}\mathrm{S}\mathrm{T}$定义为只识别一个句子。

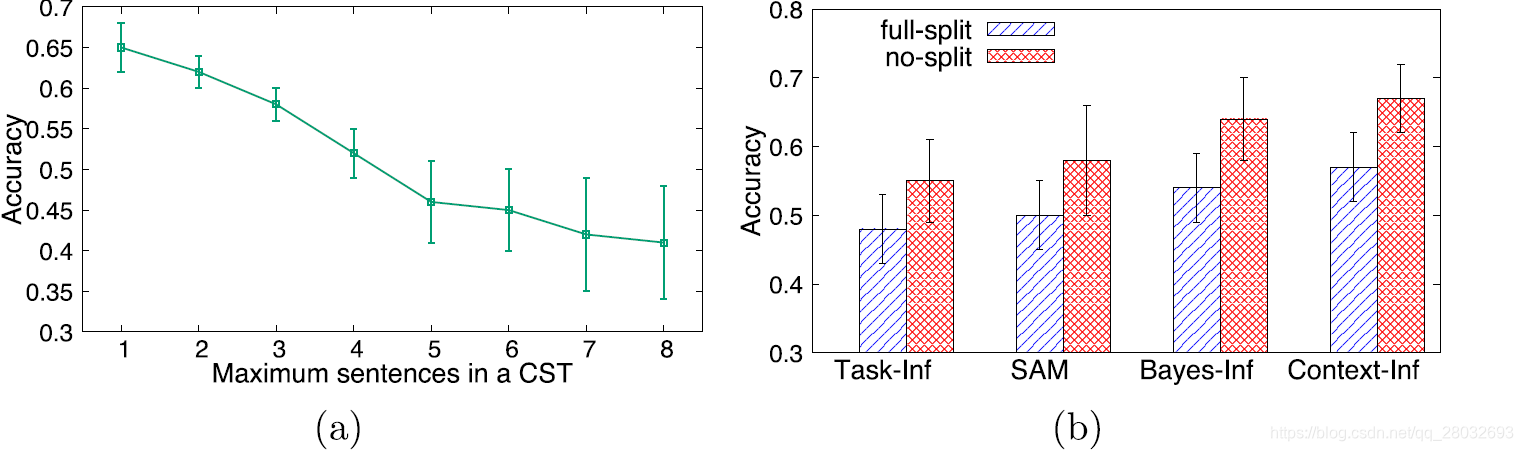
图6. 任务分割的评估；(a)不同任务分割策略的结果；(b)上下文关联的重要性

我们还进行了一项实验，以验证上下文相关是影响众包结果质量的一个重要因素。我们随机选取4张图片，共有19个句子由标点符号决定。我们比较了两种任务分割策略：无分割和完全分割。前者将每个句子作为任务发布，而后者将每个句子作为任务拆分为单独的单词。完全分割后，任务是识别图像中的一个词，所有任务都以随机顺序发布，这使得句子的上下文关联丢失。如图6(b)所示，与$\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$、$\mathrm{B}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{s}-\mathrm{I}\mathrm{n}\mathrm{f}$、$\mathrm{S}\mathrm{A}\mathrm{M}$和$\mathrm{T}\mathrm{a}\mathrm{s}\mathrm{k}-\mathrm{I}\mathrm{n}\mathrm{f}$的完全拆分相比，没有任何拆分的精确度分别提高17.54%、18.52%、16%和14.6%。

6.2.3 结果推理的有效性

接下来，我们评估了这四种推理方法在30张图像中的所有任务的性能，共有130个$\mathrm{C}\mathrm{S}\mathrm{T}$被分为6组。结果5组有20个任务，1组有30个任务。为了消除低质量工人，我们将每组任务与5个黄金任务分别混合。如果一个工人未能对5项黄金任务提供至少一个正确答案，她将被忽略。为了确保结果质量，每项任务需要得到5个答案。

图7(a)说明了用四种比较方法得到的每个任务的结果精度，图7(b)显示了每个图像的结果。我们可以看到$\mathrm{T}\mathrm{a}\mathrm{s}\mathrm{k}-\mathrm{I}\mathrm{n}\mathrm{f}$执行得最差，因为它既不考虑影响结果质量的因素，也不考虑子任务之间的上下文关联。相比之下，$\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$优于其他三种方法，因为它将上下文关联合并到$\mathrm{B}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{s}-\mathrm{I}\mathrm{n}\mathrm{f}$使用的概率模型中。$\mathrm{S}\mathrm{A}\mathrm{M}$表现优于$\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$的原因是$\mathrm{S}\mathrm{A}\mathrm{M}$可以通过考虑员工的表现更好地评估员工的能力。图7©显示了这四种方法的性能，显示$\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$比$\mathrm{B}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{s}-\mathrm{I}\mathrm{n}\mathrm{f}$、$\mathrm{S}\mathrm{A}\mathrm{M}$和$\mathrm{T}\mathrm{a}\mathrm{s}\mathrm{k}-\mathrm{I}\mathrm{n}\mathrm{f}$分别强7.76%、12.62%和43.01%。

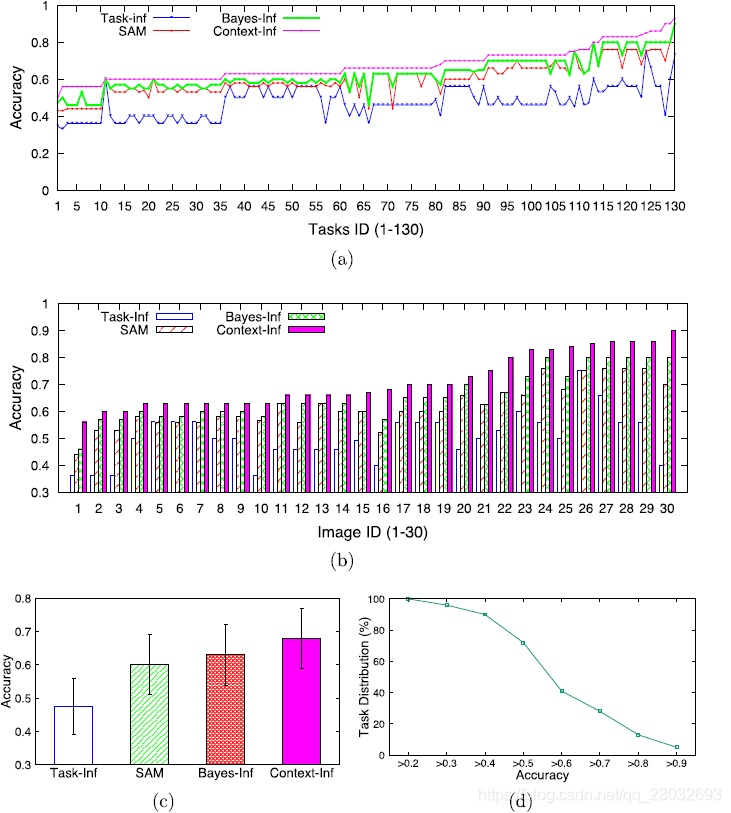
图7. 结果与结果推理；(a)所有130个任务的结果；(b)按每个图像的结果统计；(c )四种方法的总体结果；(d)处理精度的概率分布

6.2.4 迭代众包结果

图7(d)使用$\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$绘制了不同结果精度值下的任务分布。我们可以看到，超过80%的任务精度低于0.75，这意味着任务需要多轮处理。

图8描绘了$\mathrm{i}\mathrm{T}\mathrm{a}\mathrm{s}\mathrm{k}-\mathrm{I}\mathrm{n}\mathrm{f}$、$\mathrm{i}\mathrm{S}\mathrm{A}\mathrm{M}$、$\mathrm{i}\mathrm{B}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{s}-\mathrm{I}\mathrm{n}\mathrm{f}$和$\mathrm{i}\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$的实验结果。由于任务特征的不同，每个任务的迭代过程与其他任务的迭代过程有很大的不同。难度较高的任务比难度较低的任务需要更多迭代才能收敛。因此，我们首先随机选择一个$\mathrm{C}\mathrm{S}\mathrm{T}$和一个具有3个$\mathrm{C}\mathrm{S}\mathrm{T}$的图像来显示迭代处理的有效性，结果分别如图8(a)和(b)所示。我们可以观察到，众包的迭代次数越多，每个方法的结果质量就越好，经过一定次数的迭代，结果质量就不能再进一步提高。我们的方法（$\mathrm{i}\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$）比其他三种方法在迭代次数较少的情况下获得更好的质量。由于更多的迭代意味着更多的成本，我们认为以性能成本比$PCR=\frac{q_{\mathrm{T}}}{l_{\mathrm{T}}}$来衡量一种方法的有效性是公平的，其中$q_T$表示$\mathrm{C}\mathrm{S}\mathrm{T}$输出的准确性，$l_{\mathrm{T}}$表示迭代次数。图8©绘制了四种迭代方法在所有130个任务中的$PCR$。我们的$\mathrm{i}\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$仍然优于其他四个。图8(d)给出了四种迭代方法的性能$\mathrm{i}\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$的精度分别比$\mathrm{i}\mathrm{B}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{s}-\mathrm{I}\mathrm{n}\mathrm{f}$、$\mathrm{i}\mathrm{S}\mathrm{A}\mathrm{M}$和$\mathrm{i}\mathrm{T}\mathrm{a}\mathrm{s}\mathrm{k}-\mathrm{I}\mathrm{n}\mathrm{f}$高6%、8.39%和13.51%。然后，我们分别用肯德尔相关系数（Kendall Correlation Coefficients）和伦道夫系数（Randolph’s Coefficients）进行了统计检验，以显示结果的统计意义。对于130个任务，$\mathrm{i}\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$和其他三种方法（即$\mathrm{i}\mathrm{T}\mathrm{a}\mathrm{s}\mathrm{k}-\mathrm{I}\mathrm{n}\mathrm{f}$、$\mathrm{i}\mathrm{S}\mathrm{A}\mathrm{M}$和$\mathrm{i}\mathrm{B}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{s}-\mathrm{I}\mathrm{n}\mathrm{f}$）之间的肯德尔相关系数分别为0.528、0.5358和0.5765，$\mathrm{i}\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$和其他三种方法（即$\mathrm{i}\mathrm{T}\mathrm{a}\mathrm{s}\mathrm{k}-\mathrm{I}\mathrm{n}\mathrm{f}$、$\mathrm{i}\mathrm{S}\mathrm{A}\mathrm{M}$和$\mathrm{i}\mathrm{B}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{s}-\mathrm{I}\mathrm{n}\mathrm{f}$）之间的伦道夫系数分别为0.7683、0.8613和D分别为0.8986，这意味着$\mathrm{i}\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$始终优于这三种比较方法。

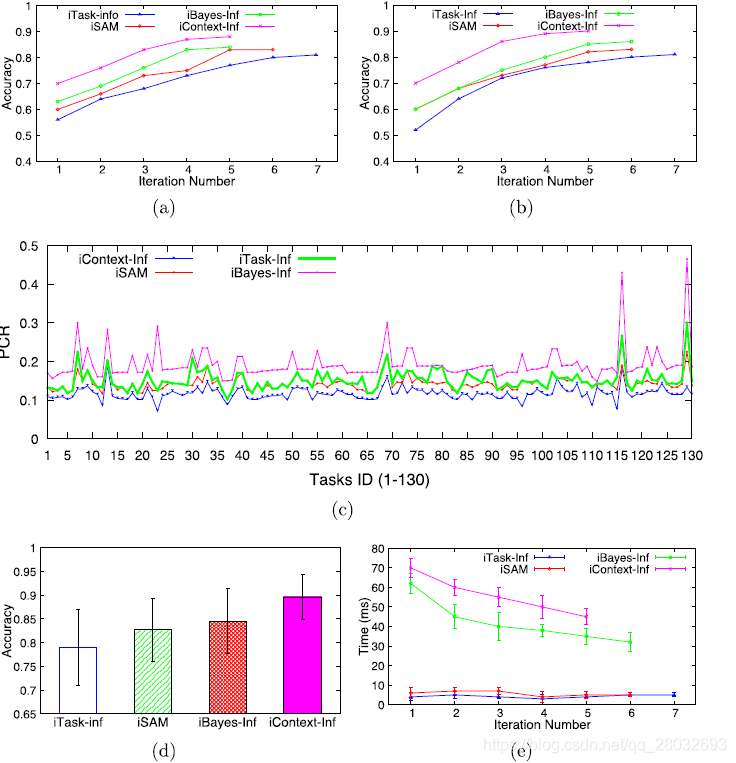
图8. 结果推断的有效性：(a)CST结果质量的迭代改进；(b)具有3个CST的图像结果质量的迭代改进；(c )迭代众包的性能成本比；(d)迭代众包的总体性能；(e)迭代众包的执行时间

图8(e)给出了四种迭代方法的执行时间。随着迭代次数的增加，要处理的子任务更少，因此所有推理方法的执行时间都缩短了。由于上下文关联计算，我们的方法在所有方法中的时间开销最大。然而，经过的时间仍在一秒钟内，这在实际应用中是可以接受的。即使花费更多的时间，我们的方法仍然可行，因为任务推断是离线执行的。

6.3 音频转录实验

6.3.1 数据集和准备工作

数据集是从CMU_ARCTIC数据库中获得的，该数据库由卡内基梅隆大学语言技术研究所构建，用于单元选择语音合成研究。我们选择了一个名为cmu-us-bdl-arctic的数据库，该数据库包含了一个特定风格的发言者发出的1200句话，共有1132个音频片段。每个剪辑包含一个句子，我们从数据库中随机选择35个剪辑，其中5个被认为是黄金测试任务。

与手写识别任务的实验设置类似，本实验每页包含10个任务，每个任务花费4美分，由5名质量等级为3的CrowdFlower工人处理。与音频剪辑相对应的子任务不能像手写任务那样直接获得，我们用OpenCV实现了这一点。当然，单词或成语之间会有停顿，这些停顿与接近零音量的部分相对应。在OpenCV中，我们分析了视频剪辑的波形，并将接近零音量的部分作为分割音频剪辑的分隔符。与手写识别实验相似，我们排除了那些无法对5个测试任务提供至少一个正确答案的工人。每项任务直到都收到5个有效答案被认为是完成的。

6.3.2 结果

图9(a)显示了这四种方法在30个任务中的结果质量。我们可以观察到与手写识别任务相似的比较结果，即$\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$优于其他三个任务。根据图9(b)所示的总体结果，我们的$\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$分别比$\mathrm{B}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{s}-\mathrm{I}\mathrm{n}\mathrm{f}$、$\mathrm{S}\mathrm{A}\mathrm{M}$和$\mathrm{T}\mathrm{a}\mathrm{s}\mathrm{k}-\mathrm{I}\mathrm{n}\mathrm{f}$好5.88%、11.11%和15.39%。毫不奇怪，如图9©所示，$\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$在这四种方法中花费的时间最多。但是，与我们对手写识别任务的分析类似，由于任务推理是离线进行的，因此有必要用额外的时间成本获得更好的结果质量。最重要的是，推理时间很短，例如只有50毫秒，这是可以接受的。

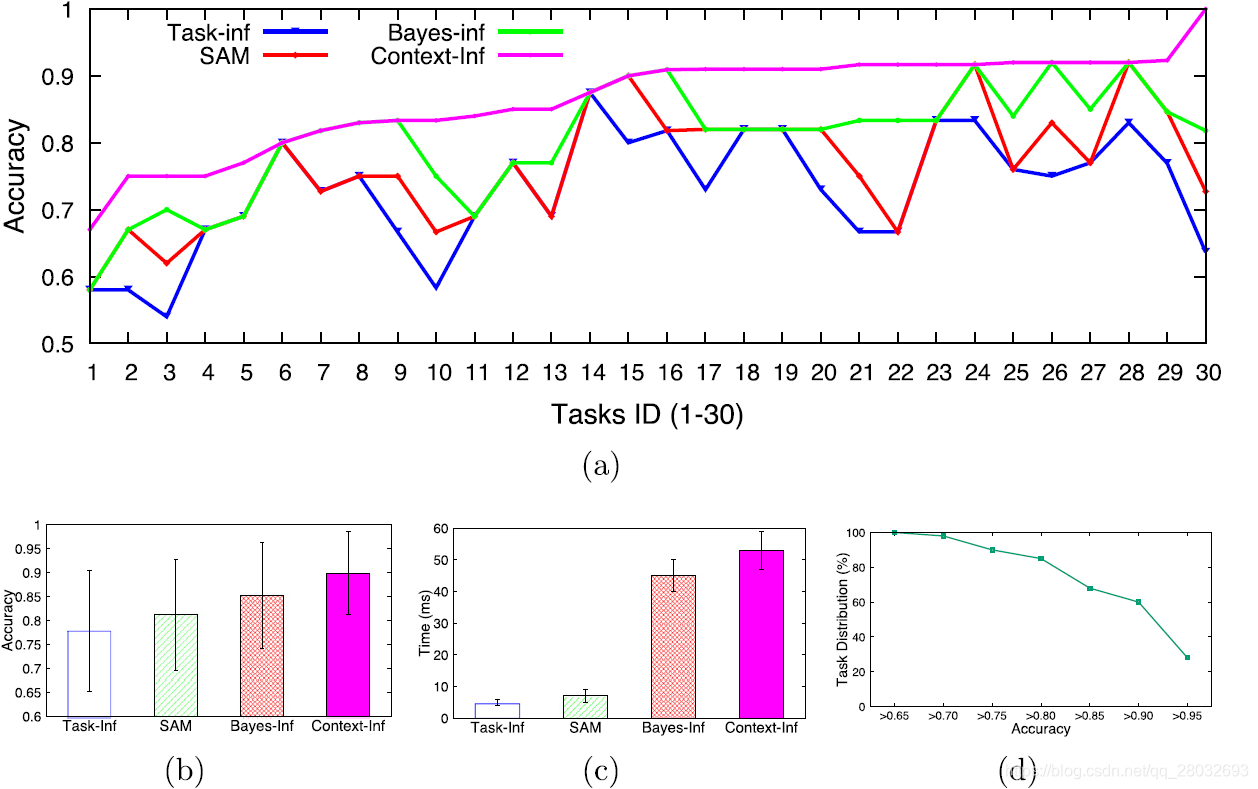
图9. 音频转录处理的结果；(2)按音频转录任务细分的结果；(b)四种方法的总体结果；(c )四种方法的执行时间；(d)具有处理精度的任务的概率分布

同时，我们给出了具有结果质量的任务的概率分布，如图9(d)所示。与手写识别任务不同，超过80%的音频转录任务的精度高达0.82。当我们继续用更多的迭代将任务众包起来时，大多数任务的结果质量不能得到很大的提高。原因是它已经达到了工人集体智慧的极限。

7 相关工作

上下文信息[6,11]是一种进化、结构化和共享的信息空间，旨在为特定目的服务，在许多不同领域的应用中发挥着重要作用。为了更好地处理任务，提出了许多考虑上下文相关的框架和模型（如[11,12,20,39]）。同样，在众包上下文中，信息主要涉及时间相关性、语义相关性、空间相关性[32]和结构化相关性。有各种各样的众包任务是上下文敏感的，例如手写识别[30]、音频描述[3]和针对人口贩运的微博[42]。然而，利用上下文信息来提高众包质量的工作很少。下面，我们从任务特征和结果推断两个方面对现有众包研究的现状进行了总结。

就结构特点而言，现有工作跨越了广泛的任务范围，可分为两大阵营：原子任务和复合任务。原子任务是指那些不能从工人那里分为子任务的任务，例如图像标记[22]、同行评分[8]和情绪分析。复合任务通常由多个原子任务组成。此外，我们将复合任务分为两个子类别：上下文敏感任务和上下文无关任务。在上下文无关的任务中，组件子任务是独立的，这意味着将其拆分为子任务或不影响质量。典型的上下文无关任务包括群组计数、群组投票和任何类型的原子任务分组。对于上下文敏感的任务，子任务之间存在着密切的关联，任务的拆分会丢失上下文关联，严重影响任务的质量。尽管大量的任务都属于这一范畴，如文本识别[26]、翻译[47]、计划[45]和音频转录[34]，但据我们所知，这并不是在结果推理中模拟上下文关联的工作。

为了进一步改进多数投票策略，有两个研究与众包任务的具体类型有关。对于孤立的任务，一些文献[18,38,48]提出了基于任务导向模型的结果推理方法（即，要求不同的工人执行相同的任务，直到对结果达成共识），以处理不准确并将成本降到最低；而对于复杂的任务，一些工作提出了基于子任务的其他推理方法。面向子任务的模型使用多阶段策略来处理任务[7,43]。CDAS[28]使用了质量敏感的回答模式。Askit[1]利用了熵样技术。Qasca研究了质量感知推理方法[52]。文献[14,16,29,50]的作者关注的是以提高结果准确性为目标的工人能力和任务主题的细粒度公式化。具体来说，为了提高推断结果的质量，Faitcrowd[29]给出了一种考虑到任务主题的更细粒度的源可靠性公式。为了提高结果的准确性，文献[14]提出了一种综合考虑源可靠性（即工人能力）和任务主题的通用细粒度方法。我们的初步工作[16]给出了一种概率方法，通过考虑备选答案之间的相似性来推断高质量的结果。文献[50]利用任务主题和工人可靠性，以外部知识库来模拟工人绩效。与这些系统相比，我们的方法考虑了任务中的上下文关联，取得了更好的结果质量。此外，为了获得工人的准确度或剔除低准确度的工人，也有许多算法通过资格考试和黄金考试来控制工人的质量，以获得匿名工人的准确度或通过考试剔除不良工人[23,38]。

与这些研究不同，我们关注的是上下文相关任务的结果推理。由于任务导向方法高估了员工处理复杂任务的能力，而子任务导向方法忽略了CST的上下文，因此无法获得高质量的结果。因此，我们提出了一种基于上下文感知的推理算法，该算法使用HMM模型来捕获任务中的上下文关联。此外，我们还提出了基于$\mathrm{P}\mathrm{O}\mathrm{M}\mathrm{D}\mathrm{P}$的迭代工作流程来改进众包的任务处理。

8 结论

本文研究了环境敏感任务的质量控制问题。我们对这类任务进行了识别，并提出了一种新的推理算法（$\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}-\mathrm{I}\mathrm{n}\mathrm{f}$），该算法结合了HMM模型来捕获结果推理的上下文相关性。利用上下文信息，利用隐马尔可夫模型进行子任务级聚合得到结果。我们还提出了一个面向众包迭代处理的$\mathrm{P}\mathrm{O}\mathrm{M}\mathrm{D}\mathrm{P}$模型。实际实验证明了该方法的优越性。

致谢

This work was supported partly by Natioanl Basic Research Program of China (2015CB358700, 2014CB340304), and NSFC program ( 61421003 ) and the State Key Laboratory of Software Development Environment under Grant No. SKLSDE-2017ZX- 14.

参考文献

[1] Y. Amsterdamer , D. Deutch , T. Milo , V. Tannen , On provenance minimization, ACM Trans. Database Syst. 37 (4) (2012) 30:1–30:36 .

[2] M. Avlonitis , I. Karydis , S. Sioutas , Early prediction in collective intelligence on video users activity, Inf. Sci. 298 © (2014) 315–329 .

[3] P.M. Baggenstoss , A modified baum-welch algorithm for hidden markov models with multiple observation spaces, Speech Audio Process., IEEE Trans. 9 (4) (2001) 411–416 .

[4] M.S. Bernstein , G. Little , R.C. Miller , B. Hartmann , M.S. Ackerman , D.R. Karger , D. Crowell , K. Panovich , Soylent: a word processor with a crowd inside, in: UIST2010, ACM, 2010, pp. 313–322 .

[5] J.A. Bilmes, et al., A gentle tutorial of the em algorithm and its application to parameter estimation for gaussian mixture and hidden markov models, ICSI TR-97-021 (1998).

[6] J. Coutaz , J.L. Crowley , S. Dobson , D. Garlan , Context is key, Commun. ACM 48 (3) (2005) 49–53 .

[7] P. Dai , C.H. Lin , Mausam , D.S. Weld , Pomdp-based control of workflows for crowdsourcing, Artif. Intell. 202 (2013) 52–85 .

[8] A. Dasgupta , A. Ghosh , Crowdsourced judgement elicitation with endogenous proficiency, in: WWW2013, ACM, 2013, pp. 319–330 .

[9] A.P. Dawid , A.M. Skene , Maximum likelihood estimation of observer error-rates using the em algorithm, Appl. Stat. (1979) 20–28 .

[10] J. Deng , W. Dong , R. Socher , L.J. Li , K. Li , L. Fei-Fei , Imagenet: a large-scale hierarchical image database, in: CVPR2009, 2009, pp. 248–255 .

[11] A.K. Dey , Understanding and using context, Pers. Ubiquitous Comput. 5 (1) (2001) 4–7 .

[12] A.K. Dey , G.D. Abowd , D. Salber , A conceptual framework and a toolkit for supporting the rapid prototyping of context-aware applications, Hum.-Comput. Interact. 16 (2) (2001) 97–166 .

[13] M. Dredze , P.P. Talukdar , K. Crammer , Sequence learning from data with multiple labels, in: ECML/PKDD, 2009, p. 39 .

[14] Y. Du , H. Xu , Y. Sun , L. Huang , A general fine-grained truth discovery approach for crowdsourced data aggregation, in: DASFAA 2017, 2017, pp. 3–18 .

[15] S.R. Eddy , Hidden markov models, Curr. Opin. Struct. Biol. 6 (3) (1996) 361 .

[16] Y. Fang , H. Sun , P. Chen , T. Deng , Improving the quality of crowdsourced image labeling via label similarity, J. Comput. Sci. Technol. 32 (5) (2017) 877–889 .

[17] Y. Fang , H. Sun , G. Li , R. Zhang , J. Huai , Effective result inference for context-sensitive tasks in crowdsourcing, in: DASFAA2016, 2016, pp. 33–48 .

[18] J. Feng , G. Li , H. Wang , J. Feng , Incremental quality inference in crowdsourcing, in: DASFAA2014, 2014, pp. 453–467 .

[19] H. Garcia-Molina , M. Joglekar , A. Marcus , A. Parameswaran , V.Verroios ,Challengesindatacrowdsourcing,IEEETrans.Knowl.DataEng.(2016) .

[20] T. Gu , H.K. Pung , D.Q. Zhang , A middleware for building context-aware mobile services, in: VTC 2004, 5, 2004, pp. 2656–2660Vol.5 .

[21] T. Han , H. Sun , Y. Song , Y. Fang , X. Liu , Incorporating external knowledge into crowd intelligence for more specific knowledge acquisition, in: IJCAI 2016„2016, pp. 1541–1547 .

[22] X. Hu, Y. Shan, G. Kesidis, S. Sarkar, R. Dhar, S. Fdida, Multiperiod subscription pricing for cellular wireless entrants (2016) 326–330.

[23] P.G. Ipeirotis , E. Gabrilovich , Quizz: targeted crowdsourcing with a billion (potential) users, in: WWW2014, 2014, pp. 143–154 .

[24] B. Lakshminarayanan, Y.W. Teh, Inferring ground truth from multi-annotator ordinal data: a probabilistic approach, arXiv: 1305.0015 (2013).

[25] G. Li , J. Wang , Y. Zheng , M.J. Franklin , Crowdsourced data management: a survey, IEEE Trans. Knowl. Data Eng. 28 (9) (2016) 2296–2319 .

[26] G. Little , L.B. Chilton , M. Goldman , R.C. Miller , Turkit: tools for iterative tasks on mechanical turk, in: Proceedings of the ACM SIGKDD Workshop on Human Computation, ACM, 2009, pp. 29–30 .

[27] Q. Liu , J. Peng , A.T. Ihler , Variational inference for crowdsourcing, in: NIPS, Curran Associates, Inc, 2012, pp. 692–700 .

[28] X. Liu , M. Lu , B.C. Ooi , Y. Shen , S. Wu , M. Zhang , CDAS: A crowdsourcing data analytics system, PVLDB 5 (10) (2012) 1040–1051 .

[29] F. Ma , Y. Li , Q. Li , M. Qiu , J. Gao , S. Zhi , L. Su , B. Zhao , H. Ji , J. Han , Faitcrowd: Fine grained truth discovery for crowdsourced data aggregation, in: SIGKDD2015, 2015, pp. 745–754 .

[30] U.V. Marti , H. Bunke , A full english sentence database for off-line handwriting recognition, in: Document Analysis and Recognition, 1999. ICDAR ’99. Proceedings of the Fifth International Conference on, 1999, pp. 705–708 .

[31] U.-V. Marti , H. Bunke ,The iam-database: an english sentence database for offline handwriting recognition, Int. J. Doc. Anal. Recogn. 5 (1) (2002) 39–46 .

[32] V.G. Motti , J. Vanderdonckt , A computational framework for context-aware adaptation of user interfaces, in: IEEE Seventh International Conference on Research Challenges in Information Science, 2013, pp. 1–12 .

[33] Y. Normandin , Maximum Mutual Information Estimation of Hidden Markov Models, Springer US, 1996 .

[34] G. Parent , M. Eskenazi , Toward better crowdsourced transcription: transcription of a year of the let’s go bus information system data, SLT, 2010 .

[35] L.R. Rabiner , A tutorial on hidden markov models and selected applications in speech recognition, Proc. IEEE 77 (2) (1989) 257–286 .

[36] L.R. Rabiner , Readings in Speech Recognition, Morgan Kaufmann Publishers Inc., 1990 .

[37] R.A. Robb , Biomedical Imaging, Visualization, and Analysis, John Wiley & Sons, Inc., 1999 .

[38] M. Salek , Y. Bachrach , P.Key ,Hotspotting–aprobabilisticgraphicalmodelforimageobjectlocalizationthroughcrowdsourcing,AAAI2013,2013 .

[39] W. Shen , J. Han , J. Wang , A probabilistic model for linking named entities in web text with heterogeneous information networks, in: SIGMOD2014, 2014, pp. 1199–1210 .

[40] V.S. Sheng , F. Provost , P.G. Ipeirotis , Get another label? improving data quality and data mining using multiple, noisy labelers, in: SIGKDD2008, ACM, 2008, pp. 614–622 .

[41] A. Sheshadri , M. Lease , Square: a benchmark for research on computing crowd consensus., in: B. Hartman, E. Horvitz (Eds.), HCOMP, AAAI, 2013 .

[42] K. Starbird , Delivering patients to sacrécoeur: collective intelligence in digital volunteer communities, in: CHI2013, ACM, 2013, pp. 801–810 .

[43] L. Tran-Thanh , T.D. Huynh , A. Rosenfeld , S.D. Ramchurn , N.R. Jennings , Crowdsourcing complex workflows under budget constraints, in: AAAI2015, 2015, pp. 1298–1304 .

[44] L. Von Ahn , B. Maurer , C. McMillen , D. Abraham , M. Blum , recaptcha: human-based character recognition via web security measures, Science 321 (5895) (2008) 1465–1468 .

[45] Y. Wang , J. Jiang , T. Mu ,Context-aware and energy-driven route optimization for fully electric vehicles via crowdsourcing, IEEE Trans. Intell. Transp. Syst. 14 (3) (2013) 1331–1345 .

[46] J. Whitehill , P. Ruvolo , T. Wu , J. Bergsma , J. Movellan , Whose vote should count more: optimal integration of labels from labelers of unknown expertise, in: NIPS2009, 2009, pp. 2035–2043 .

[47] O.F. Zaidan , C. Callison-Burch , Crowdsourcing translation: professional quality from non-professionals, in: HLT ’2011, 2011, pp. 1220–1229 .

[48] J. Zhang , V.S. Sheng , Q. Li , J. Wu , X. Wu , Consensus algorithms for biased labeling in crowdsourcing, Inf. Sci. 382383 (2017) 254–273 .

[49] J. Zhang , X. Wu , V.S. Sheng , Learning from crowdsourced labeled data: a survey, Artif. Intell. Rev. 46 (2016) 1–34 .

[50] Y. Zheng , G. Li , R. Cheng , DOCS: domain-aware crowdsourcing system, PVLDB 10 (4) (2016) 361–372 .

[51] Y. Zheng , G. Li , Y. Li , C. Shan , R. Cheng , Truth inference in crowdsourcing: is the problem solved? PVLDB 10 (5) (2017) 541–552 .

[52] Y. Zheng , J. Wang , G. Li , R. Cheng , J. Feng , QASCA: a quality-aware task assignment system for crowdsourcing applications, in: SIGMOD2015, 2015, pp. 1031–1046 .