二分查找 & 二叉搜索树 & 平衡二叉搜索树（AVL树）

1. 二分查找

定义：基于有序顺序表的查找，时间复杂度O(logN)

//非递归
int binarySearch(int a[], int key)
{
	int left=0, right = a.size()-1;
	while(left<=right)
	{
		int mid = left + (right-left)/2;
		if(a[mid] == key) return mid;
		else if(a[mid]>key) right =  mid-1;
		else left = mid+1;
	}
	return -1;
}
//递归
int BinarySearch(int left, int right)
{
	if(left > right) return -1;
	int mid = left+(right-left)/2;
	if(a[mid]==key) return mid;
	else if(a[mid]>key) return BinarySearch(left, mid-1);
	else return BinarySearch(mid+1, right);
}

2. 二叉搜索树

（1） 定义

左子树的所有结点小于根结点，右子树的所有结点大于根结点。左子树和右子树也是二叉搜索树。

（2）性质

二叉搜索树的中序遍历为从小到大排列的。

（3）搜索

//递归搜索
TreeNode* search(TreeNode* root, int key)
{
	if(root == NULL) return NULL; //没有找到
	if(root->val == key) return root;
	else if(root->val > key) search(root->right, key);
	else search(root->left, key);
}

（4）插入

从根节点出发，查找要插入的位置。若已经存在，则退出；否则，插入到该位置。

//递归插入
void insert(TreeNode* &root, int k) //注意root为引用
{
	if(root == NULL) //找到插入的位置
	{
		root = new TreeNode(k);
		return;
	}
	else if(root->val == k) return; //已有该元素
	else if(root->val > k) insert(root->left, k);
	else insert(root->right, k);
}

（4）删除

3. 平衡二叉搜索树(AVL树)

（1）定义

左子树和右子树的高度差不超过1，且左子树和右子树也为AVL树。
平衡因子：每个结点有一个平衡因子，等于右子树的高度-左子树的高度。

（2）插入

插入操作和二叉搜索树一致。但是在插入后，要从插入位置向上回溯，检查各节点的平衡因子，若绝对值大于1，则要进行平衡化旋转。

（3）平衡化旋转

• 左旋

void rotateL(TreeNode* &root)
{
	TreeNode* subL = root;
	root = root->right;
	subL->right = root->left;
	root->left = subL;
	root->bf = subL->bf = 0;
}

• 右旋

void rotateR(TreeNode* &root)
{
	TreeNode* subR = root;
	root = root->left;
	subR->left = root->right;
	root->right = subR;
	root->bf = subR->bf = 0;
}

• 左右旋
  左孩子的右子树中插入节点导致的不平衡。

void rotateLR(TreeNode* &root)
{
	TreeNode* subR = root;
	TreeNode* subL = root->left;
	root = subL->right;
	subL->right = root->left;
	root->left = subL;
   if(root->bf <=0) subL->bf=0;
   else subL->bf = -1;
   subR->left = root->right; 
   root->right = subR;
   if(root->bf==-1) subR->bf = 1;
   else subR->bf = 0;
   root->bf=0;
}

• 右左旋
  右孩子的左子树中插入结点导致的不平衡

void rotateRL(TreeNode* &root)
{
  TreeNode* subL = root;
  TreeNode* subR = root->right;
  root = subR->left;
  subR->left = root->right;
  root->right = subR;
  if(root->bf <=0) subR->bf=0;
  else subR->bf = -1;
  subL->right= root->left 
  root->left = subL;
  if(root->bf==-1) subL->bf = 1;
  else subL->bf = 0;
  root->bf = 0;
}

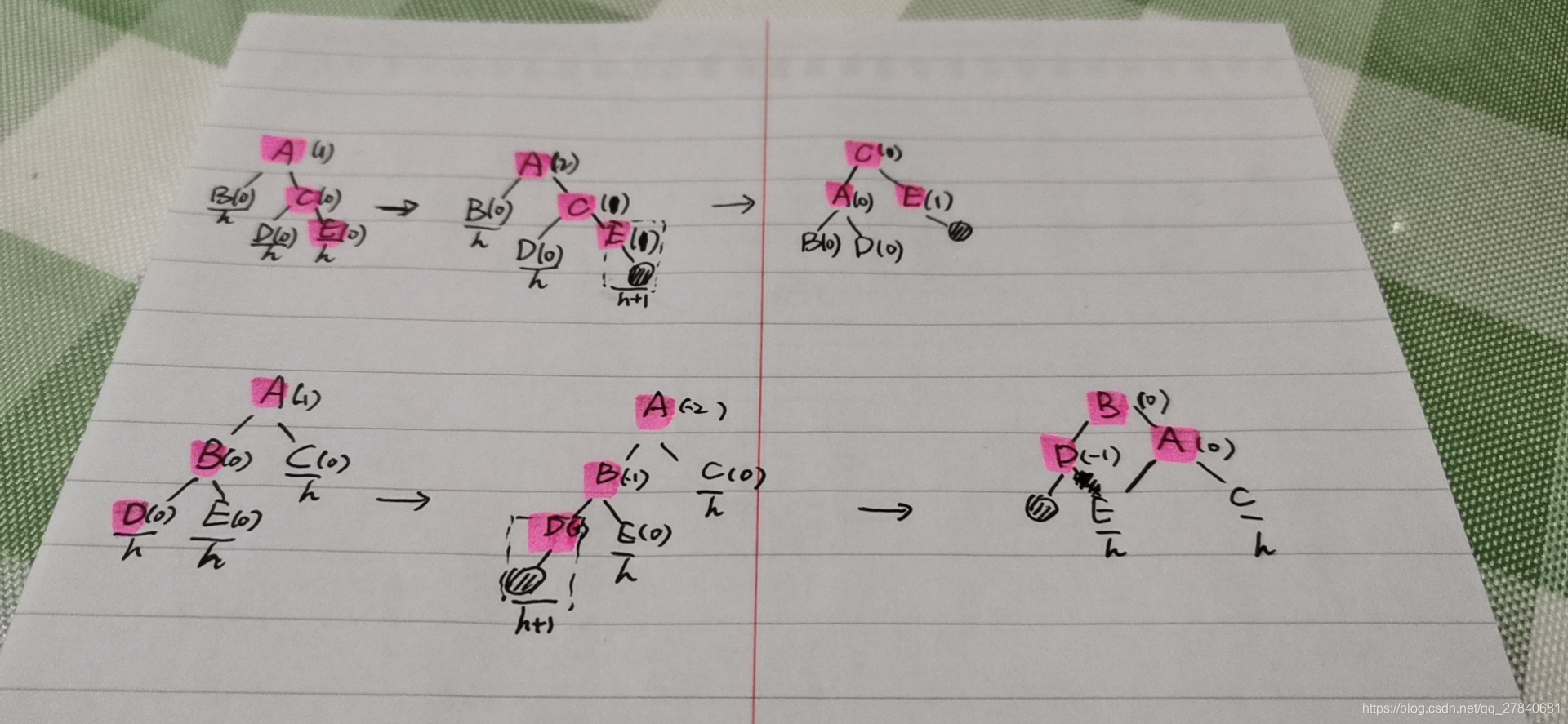
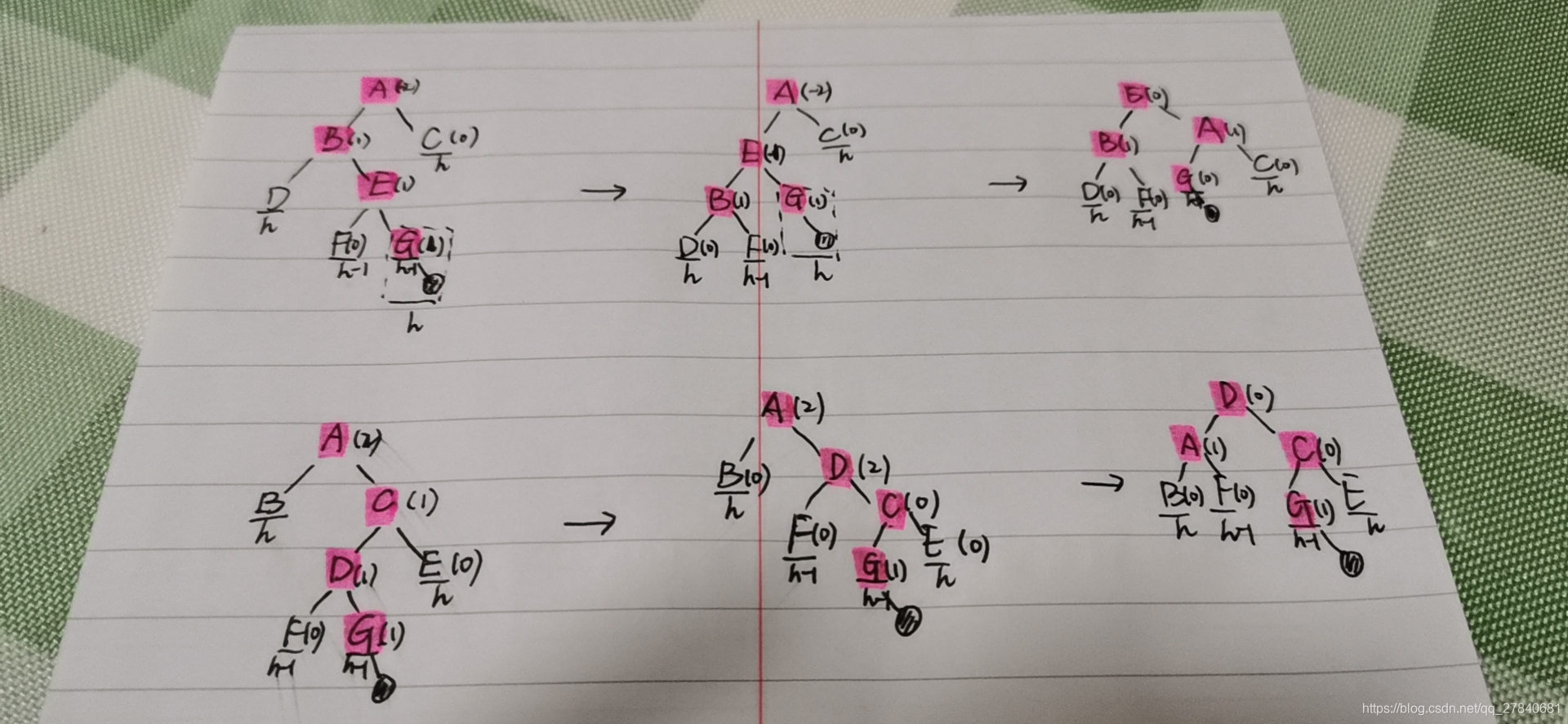
(4)删除

(5) 性质

• 插入和删除某个结点，并做平衡化旋转的时间复杂度为O(logN)。
• 对于频繁的插入和删除操作，平衡二叉搜索树不适合。
• 二叉搜索树适合于组织在内存中较小的索引（或目录）。
• 对于外存中较大的文件系统，用B树或B+树更合适。