数据结构与算法 | 7-顺序表

1 前言

在之前的一期博客中提到过线性表，具体见：数据结构与算法 | 6-线性表 ，里面提到线性表的概念为：

那本期要提到的顺序表和线性表有什么关系呢？

实际上，根据线性表的实际存储方式，分为两种实现模型：

• 顺序表。将元素顺序地存放在一块连续的存储区里，元素间的顺序关系由它们的存储顺序自然表示。
• 链表。将元素存放在通过链接构造起来的一系列存储块中。

2 什么是顺序表

2.1 顺序表的基本形式

根据元素的位置，顺序表的基本形式可以分为下面两种：

• 元素内置顺序表
• 元素外置顺序表

2.1.1 基本知识补充

• 整数占4个字节，即4个存储单元

• 字符占1个字节，即1个存储单元

• 1个字节是8位，4个字节是32位，也就是有32个小格子来存储数据，具体见下图：
  
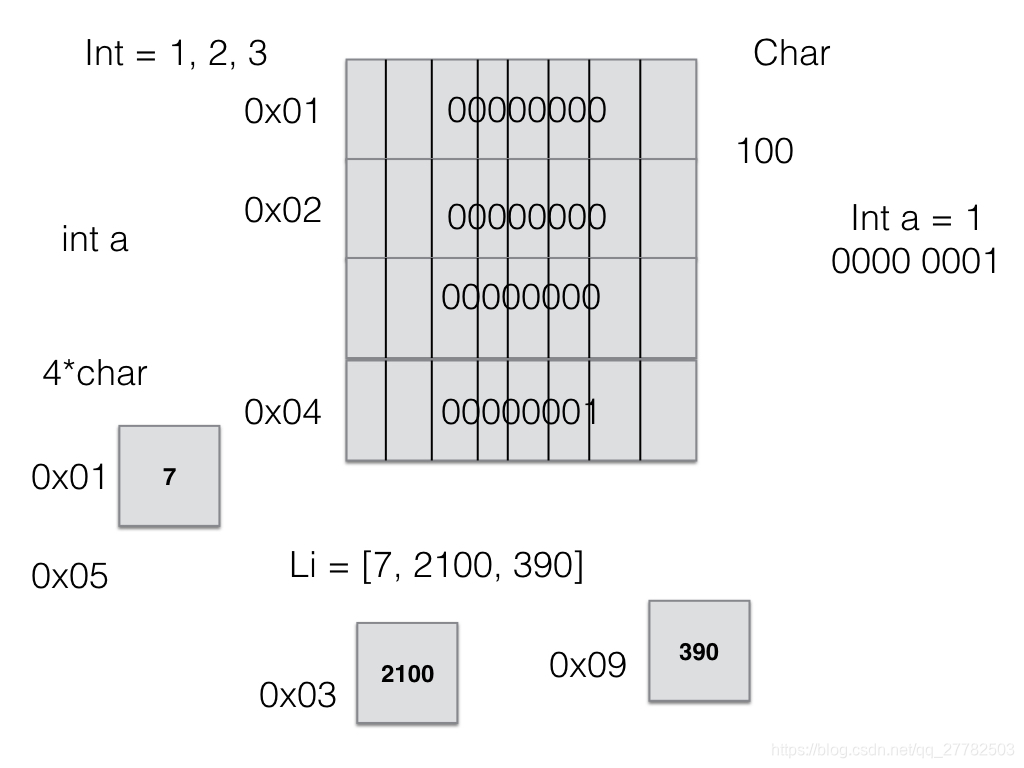
  上图这32个小格子（4*8）就代表了整数1在内存中的存储方式。

• 不论是整数还是字符，都属于变量的不同类型，那变量类型的本质是啥呢？

  • 一是变量类型决定了该变量占多少内存
  • 二是一开始存储该数据的时候就需要指定类型

2.1.2 元素内/外置顺序表

关于元素内/外置顺序表，具体见下图：

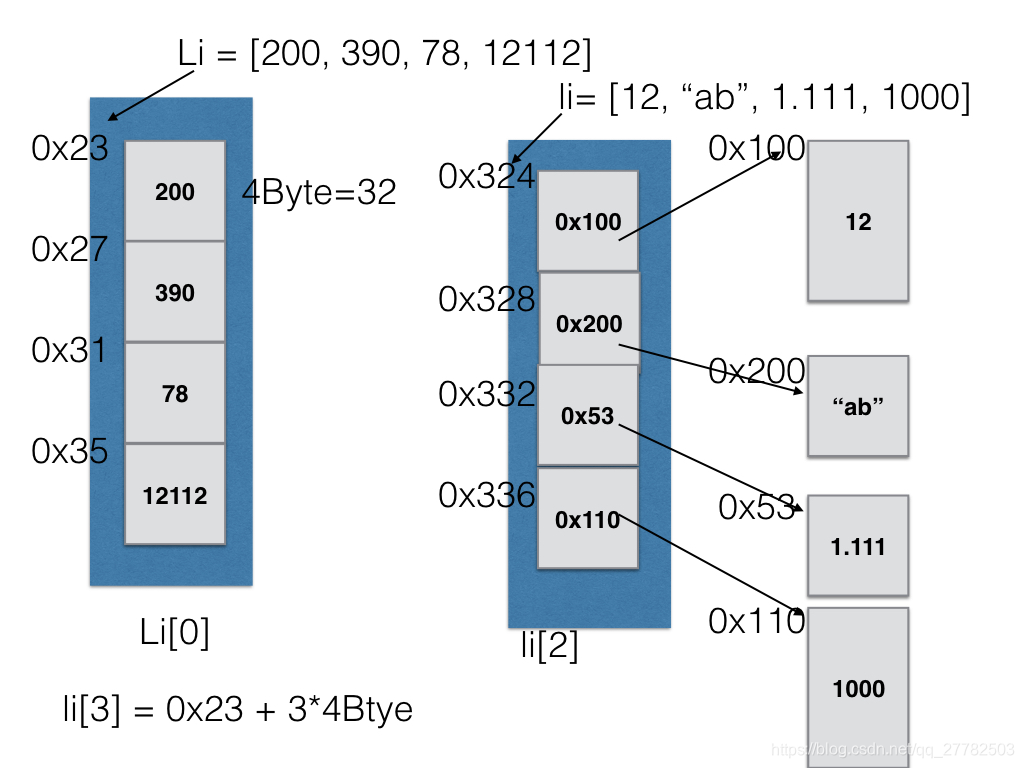
• 左边图形表示元素内置的顺序表，右边则是外置。

想必大家肯定会问，为什么会有这两种顺序表的差异呢？本质原因就是顺序表里存储的数据的类型是否一致导致的！如果不一致，就会出现右边的元素外置情形，如果顺序表中数据类型都一样，就可以直接使用左边的形式。

不懂就问，那为什么顺序表中数据类型不一致就不能使用左边的形式呢？因为不同类型数据
存储占得字节不一样，所以无法像左边一样按顺序来。

左边元素内置情况下：

数据查询时候的逻辑为：

• 第一个元素Li[0] = 200，对应位置OX23，如果想要查询第3个元素，直接就是：

位置：OX23 + 3 * Byte4 = OX35 对应的元素12112，即 Li[3] = 12112

• 上述公式中3表示偏移量。解释了为什么计算机从0开始计数，表示没有偏移量，i表示偏移量为i
• Byte4表示相应数据类型所占字节数！本例中由于是整数，所以占4个字节！
• 上述计算公式可以抽象为：
  

右边元素外置情况下：

先考虑为什么这么存储！

上面也提到过，由于顺序表中数据的类型不一致，所以无法像左边直接按照位置元素内置进行存储（此时元素位置不连续），那怎么考虑呢？比较自然的想法就是：

• 将此时顺序表中的元素的位置进行内置存储！即存储的不是元素，而是元素的位置了！
• 然后再对元素的位置按照左边的方式进行存储，此时位置连续！

此时数据查询时候的逻辑为：

• 第一个元素Li[0] = 12，对应位置OX324，内置存储的元素为OX100，而OX100对应的外置元素为12，查询完毕。
• 如果想要查询第3个元素，直接就是：OX324 + 3 * Byte4 = OX336，而OX336的内置元素为OX110，其对应的外置元素为1000，即Li[3] = 1000，查询完毕。

2.2 顺序表的结构和实现方式

2.2.1 结构

关于顺序表的结构，上面我们看到了主要的部分，也就是数据是如何存储的，那顺序表中是不是只有存储的数据呢？答案很显然不是，具体的结构包括两部分：

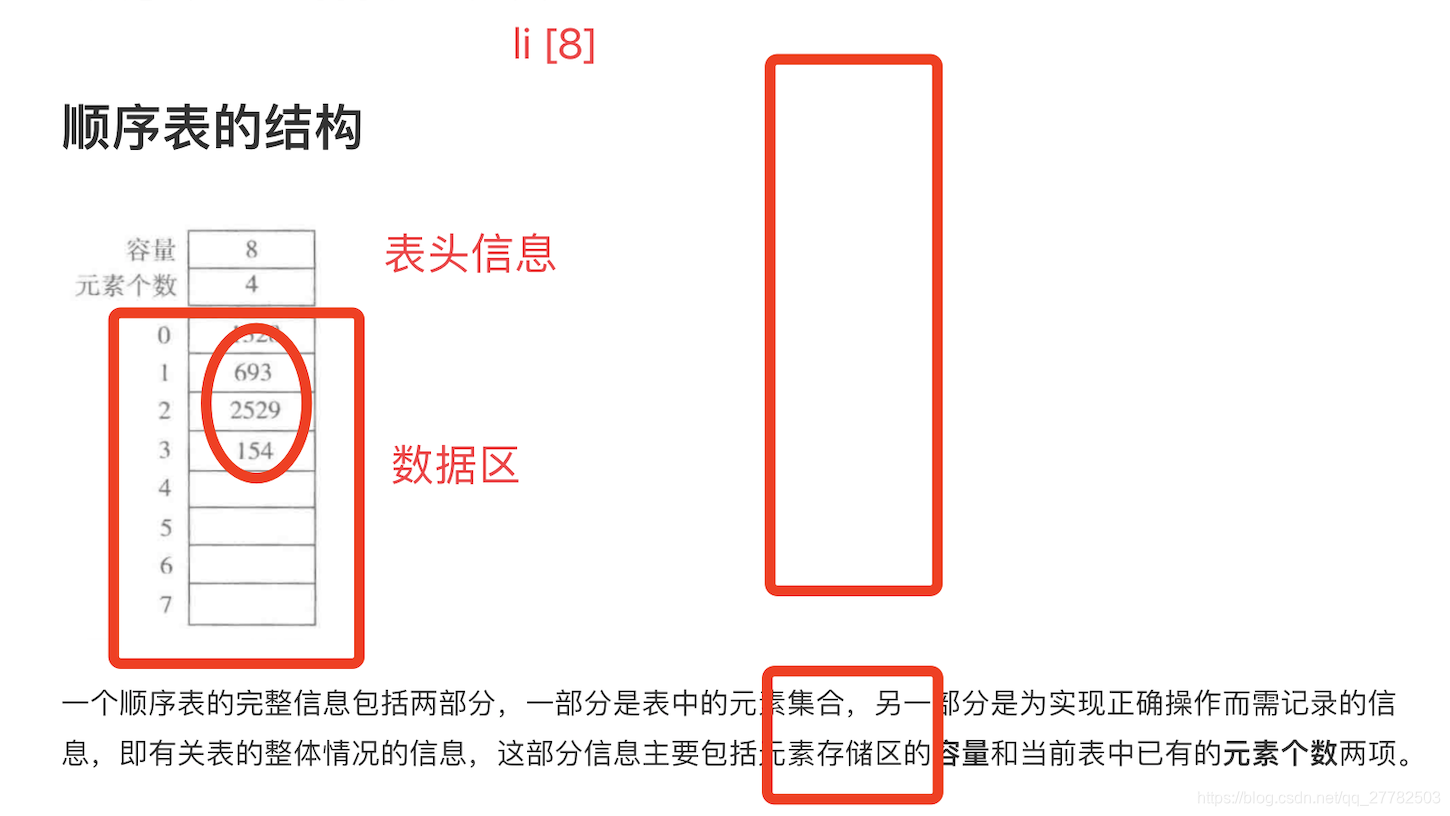
即表头信息+数据区！其中表头信息又包括两部分：

• 容量。即顺序表最多能存储多少个数据
• 元素个数。即顺序表现在已经存储了多少个数据了！

2.2.2 实现方式

什么叫实现方式？也就是表头信息和数据区如何组装在一起？是缠缠绵绵绕天涯还是分居两地？哈哈，分别对应的就是两种结构：

• 一体式结构。即表头信息和数据区在一块存储区里。

• 分离式结构。即顺序表中只存放表头信息，而数据放在独立的存储区中，通过顺序表中第三个位置信息，即链接实现和数据的关联。
  
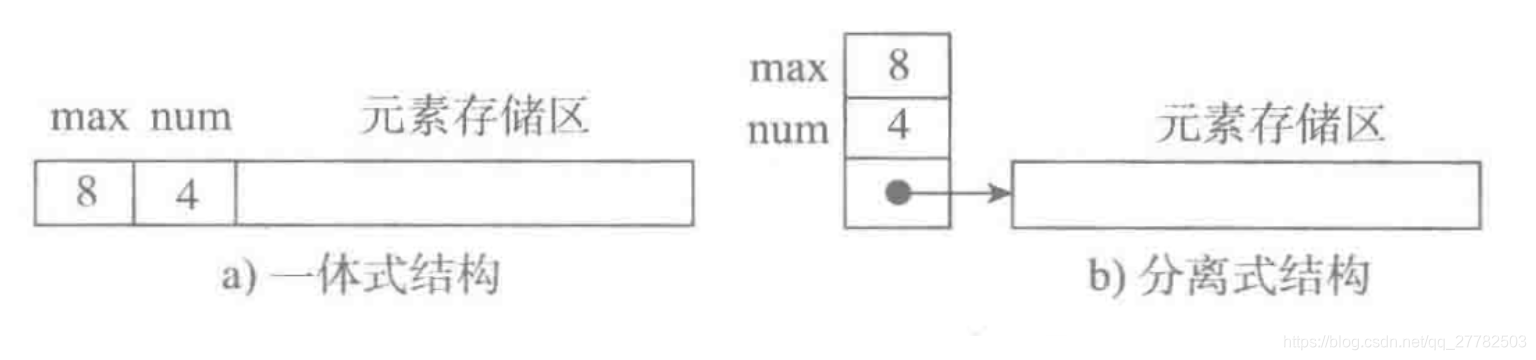
  那这两种实现方式哪一种更好呢？分离式结构！

• 存储区替换时，分离式结构直接改变存储区以及顺序表中第三个位置的链接即可，而对于一体式结构则只能整体搬迁，即整个顺序表对象（指存储顺序表的结构信息的区域）改变了。

• 存储区扩容时，分离式结构的表头信息不会发生变化，只需改变第三个位置的链接，即扩容后数据的首位置信息。而一体式结构需要改变所有的信息，无论是表头的还是数据区。
  

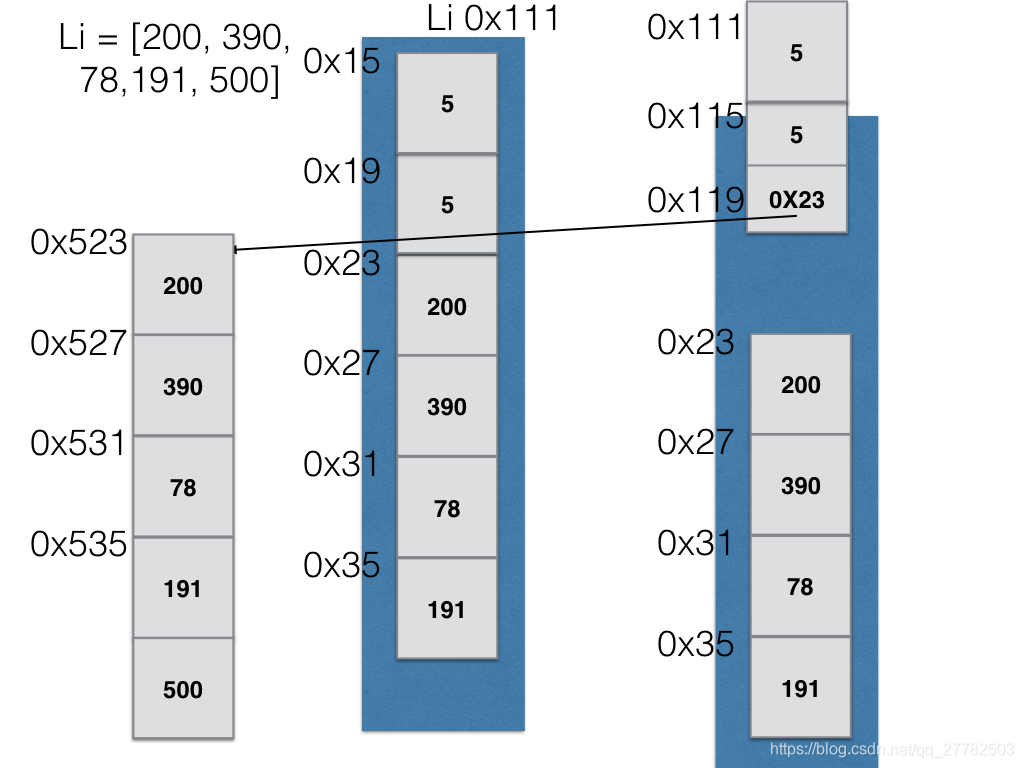
注1：在Python的官方实现中，list就是一种采用分离式技术实现的动态顺序表。

上面提到存储区扩容，对于扩容，有着两种不同的扩容策略！

• 策略1：固定数目扩容。
  • 优点：所需空间少
  • 缺点：如果频繁需要扩充而空间又每次不够的时候，需要消耗的时间成本较大。
• 策略2：加倍扩容。【一般采用】
  • 优点：时间成本较少，一次到位。4→8→16→32…
  • 缺点：空间换时间。空间成本较高，但一般都会选择这么做，保证时间效率！

注2：在Python的官方实现中，list实现采用了如下的策略：
在建立空表（或者很小的表）时，系统分配一块能容纳8个元素的存储区；在执行插入操作（insert或append）时，如果元素存储区满就换一块4倍大的存储区。但如果此时的表已经很大（目前的阀值为50000），则改变策略，采用加一倍的方法。引入这种改变策略的方式，是为了避免出现过多空闲的存储位置。

参考

• b站视频：https://www.bilibili.com/video/av53583801/?p=11