对Batch_Normalization的理解

大家都说batch normalization 具有

1)加快网络收敛

2)使训练更加稳定(即对参数的初始化和学习率不敏感)

的作用，但是在阅读BNs的原文之前，笔者对上面的两个作用的理解也只是停留在文字层面，在阅读完原文之后对BNs有了一个比较具体的认识，今天我们就来探究以下BNs是怎么实现上述的两个作用的。

在此之前，建议大家先看看知乎上对于BNs的高票回答，大佬们对于BNs的算法讲解的还是比较清晰的：

BNs的算法如下所示，

总结以上算法，就是:

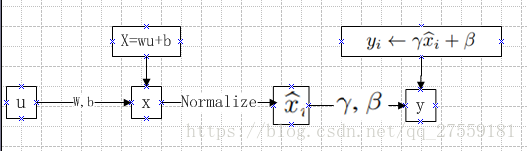
w,b在算法Algorithm 1中没有写出来，其实它是在x之前的。

对于上面的BNs我们会有下面几个问题：

1.为什么要做这个Normalize呢？

    这是因为，如果没有做Normalize，x(这里的x是指即将进入到神经网络下一层的输入)的绝对值很可能会大于1，这样的话，对于softmax激活函数，很可能会造成梯度弥散，这样一来训练速度就会变得非常慢，尤其是对靠前面的网络层。

2.为什么要加一个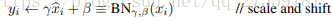，直接normalize不就完事了吗。

如果只把x归一化到(0,1)之间，会使得x都集中在softmax激活函数的线性区域：

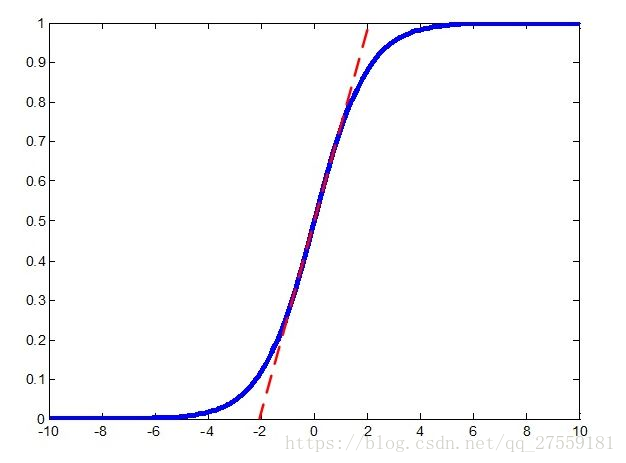
这样等价于没用非线性函数了，这样网络就难以拟合非线性函数了，原文的表述是这样的:

                             

    但是上面的解释还是不够充分，笔者有一个与知乎用户一样的问题：

对于上面的问题，答主的回答是：

但笔者认为这个回答还是没回答笔者的问题：

如果在非线性操作之前通过scale and shift又将均值为0的输入变为均值不为0(比如大于1的均值)，这不是又会使得在反向传播的时候导致梯度弥散吗？

而笔者的推断是：

事实上采用BNs之后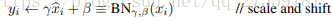中的y的分布仍然会比较接近0，即y的均值仍然会比较接近0，证据如下图：

(b,c)中的x分布是神经网络中最后一个隐层的输入，可以看到没有BNs，刚开始训练时，x的分布逐渐偏移原点，而加了BNs之后，x的均值都相对集中在0附近(这是一个非常好的性质,可以使得梯度不容易弥散)，

那有个问题，为什么没加BNs的话，开始训练时，x的分布会逐渐远离原点0呢？

原理如下图：

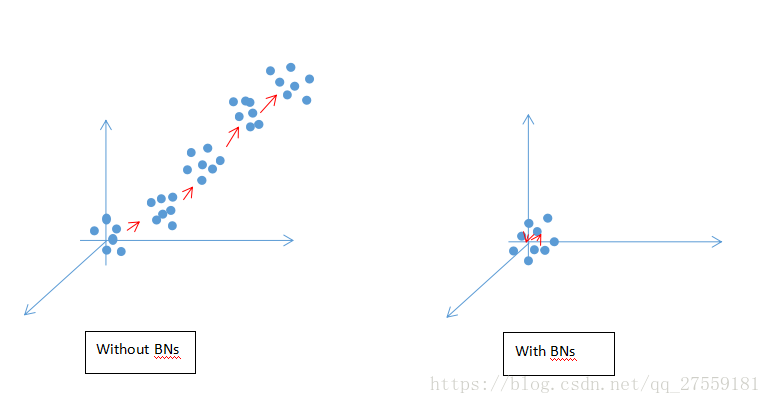
x的分布可能会因为训练参数w，b的一些微小变化而导致分布也朝着某个反向(图中红色箭头)发生微小的移动(就是论文中反复提到的Internal Covariance Shift)，而我们假设这个微小移动的方向是随机的，试想一下经过多次微小移动之后，x分布还在原点附近的概率更高，还是在偏离原点的位置的概率更高，很明显x分布还在原点附近的概率将会变得越来越低，而BNs则是在每次x输入到激活函数之前，做一个归一化，使得这个Internal Covariance Shift被eliminated，这样x的分布还在原点附近的概率将大大提升，从而使得反向传播中的梯度不易弥散，使得训练速度大幅提升。

事实上BNs还有一些很骚的作用(比如文章提到的可以取代dropout的一些性能等等)，具体大家可以看看原文。