【排序】图解归并排序

一、思想

一句话总结：先拆分，后按顺序合并。

归并排序是创建在归并操作上的一种有效的排序算法，该算法是采用分治法的一个非常典型的应用。主要的思想为「分而治之」，将大问题化解成一个个的小问题，逐个求解，最后将这些结果组合到一起。

二、图解过程

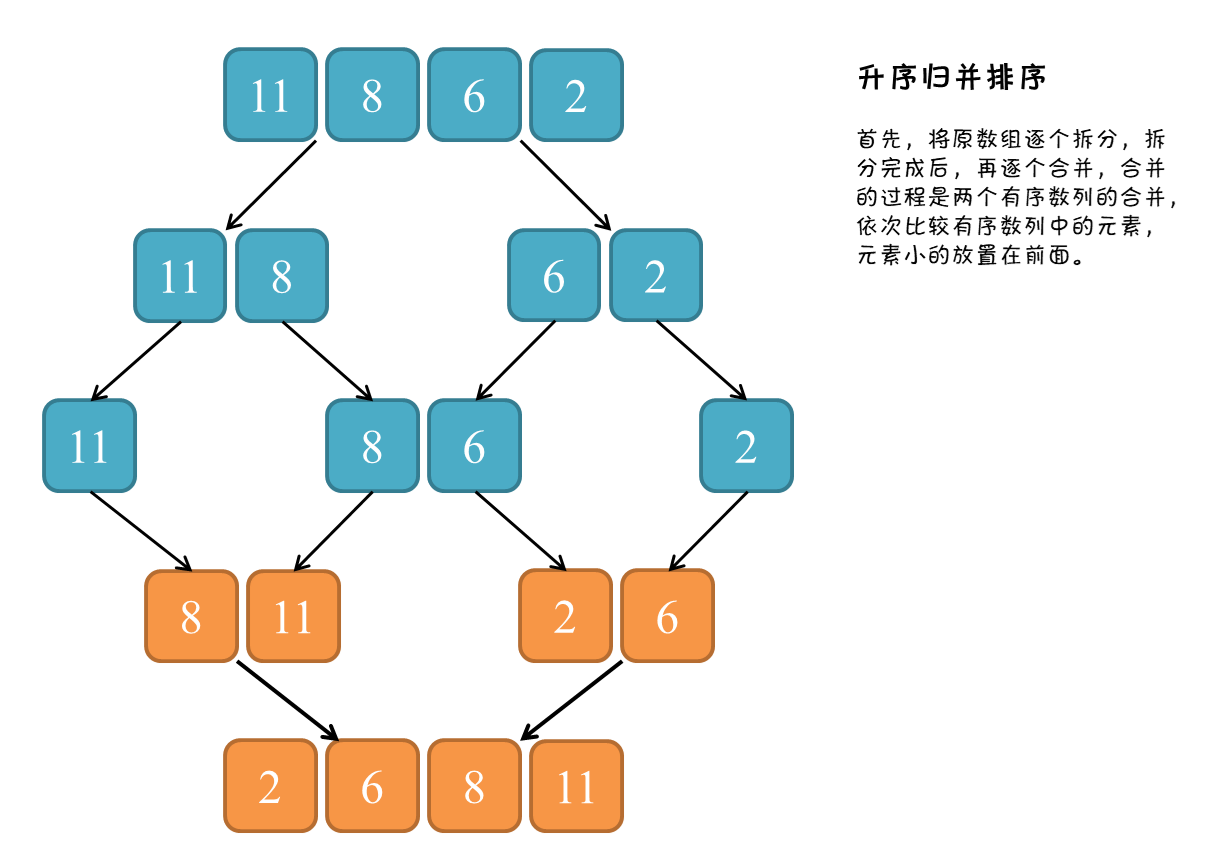
三、核心代码

//归并排序
public static void mergeSort(int[] arr) {
	if (arr == null || arr.length < 2) {
		return;
	}
	mergeSort(arr, 0, arr.length - 1);
}
//分治
public static void mergeSort(int[] arr, int l, int r) {
	if (l == r) {
		return;
	}
	int mid = l + ((r - l) >> 1);
	mergeSort(arr, l, mid);
	mergeSort(arr, mid + 1, r);
	merge(arr, l, mid, r);
}
//合并
public static void merge(int[] arr, int l, int m, int r) {
	int[] help = new int[r - l + 1];
	int i = 0;
	int p1 = l;
	int p2 = m + 1;
	while (p1 <= m && p2 <= r) {
		help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
	}
	while (p1 <= m) {
		help[i++] = arr[p1++];
	}
	while (p2 <= r) {
		help[i++] = arr[p2++];
	}
	for (i = 0; i < help.length; i++) {
		arr[l + i] = help[i];
	}
}

四、复杂度分析

1、时间复杂度：O(NlogN)

每次合并的操作时间复杂度为 $O(N)$，完全二叉树深度为 $lo{g}_{2}N$。最好、最坏、平均时间复杂度为均为 $O(NlogN)$。

平均速度比快速排序慢，虽然都是$O(NlogN)$，但是归并排序操作次数正比于数列长度，常数系数更大。

2、额外空间复杂度：O(N)

合并时借助了一个数组进行外排。

五、稳定性分析

每次归并确保相同的数，第一个数列的先加入，所以归并排序是稳定的，这是相对快速排序的一大优势。