基础知识-因果分析-dayfive-一元线性回归

当线性回归函数f(X)中只有一个变量时，称为一元线性回归。我们将关于两个随机变量X和Y的样本数据集(xi,yi)以散点图的形式画在以变量X为X轴、以需要预测的变量Y为Y轴的直角坐标平面上，用线性回归函数f(X)对预测变量Y进行近似，就是在该直角坐标平面上用一条直线对散点图进行拟合，如图2.1所示。假设回归函数为f(X)=a+bX，则根据回归函数得到的Y变量预测值

根据中心极限定理，Y与f(X)的误差ε通常服从正态分布，则当Y变量的预测值与实际值之差的平方和最小时，线性回归函数f(X)对预测变量Y有最好的近似，即下式最小化

将式(2.24)分别对a和b求偏导，并令其为零，则可以求得回归函数为Y=a+bX的具体表达式，该方法称为最小二乘法，这里不做详细介绍。

我们也可以求得回归函数中系数b与变量X和Y的数字特征的关系。根据线性回归假设，有

等式(2.25)两边对变量X做协方差，则有

cov(Y,X)=cov(a,X)+bcov(X,X)+cov(ε,X)

根据协方差的性质有cov(a,X)=0，根据前述假设有cov(ε,X)=0，故有cov(Y,X)=bcov(X,X)=bvar(X)

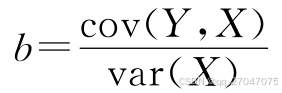
一般将b表示为RYX，称为回归系数，也就是拟合直线的斜率，则有

对等式(2.25)两边分别取期望，则有E(Y)=E(a)+E(bX)+E(ε)E(Y)=a+bE(X)+E(ε)则有a+E(ε)=E(Y)-bE(X)令E(ε)=0（ε均值的大小可以通过调整a的取值来体现）​，则有

一般情况下var(X)≠var(Y)，所以一般RYX≠RXY，即变量Y关于变量X回归的斜率不等于变量X关于变量Y回归的斜率。由于方差始终为正，而相关系数可为正、负或0，因此变量Y关于变量X回归（或相反）的斜率也可为正、负或0。若斜率为正，则两个变量正相关，当变量X增加时变量Y也会增加；若斜率为负，则两个变量负相关，当变量X增加时变量Y会减少；若斜率为0，即回归的直线为水平直线，则变量X和变量Y零线性相关，在做线性预测时，已知变量X的取值对于预测变量Y的取值没有任何帮助。两个变量无论是正相关还是负相关，它们都是相互依赖的。

多元线性回归

将线性回归从一个变量对另一个变量的预测推广到用多个变量对另一个变量的预测，称为多元线性回归，也称为一个变量相对多个变量做线性回归。我们主要以二元线性回归为例，对多元线性回归进行介绍。在二元线性回归中，我们希望根据变量X和Z的值来预测变量Y的值，相应的回归函数表达式如下：

这个回归函数表达式在X、Y、Z三维空间表现为一个倾斜的平面。如已知关于变量{X,Y,Z}的样本数据集，将这些样本表现为以X、Y和Z为坐标的三维空间的散点图形式，则用式(2.28)对变量Y进行近似，就是在以X、Y和Z为坐标轴的三维空间，用回归函数表达式所对应的倾斜平面对散点图进行拟合，如图2.2所示。

当我们在三维空间中将散点图按照不同的Z变量取值切片时，得到一个X-Y二维平面上的散点图，根据二维平面上的散点图将变量Y对变量X做回归，则问题转化为一元线性回归问题，相应斜率为式(2.28)

回归表达式中的r1，满足一元线性回归中的式(2.25)。同理，将三维散点图按不同的X变量取值切片，并在相应的Z-Y二维散点图上做回归，可以得到式(2.28)回归表达式中相应的斜率r2。上述在Z变量取值固定的条件下，变量Y相对变量X的回归系数称为偏回归系数，记为RYX-Z。值得注意的是，在同一个关于{X,Y,Z}的样本数据集下，可能出现这样的情况：当只分析X和Y两个变量数据的时候，对应的回归系数RYX为正；而当分析加上另外一个变量Z的数据且变量Z取值固定时，对应的偏回归系数RYX-Z为负。这就是辛普森悖论在数学上的表现：只分析X和Y两个变量的数据时，变量Y和变量X为正相关（负相关）​，但当分析加上第三个变量Z的数据且以变量Z取一定值为条件时，则结论相反，变量Y与变量X变为负相关（正相关）​。比如，在大学入学性别歧视的例子中，当只分析性别与录取率的数据时，我们发现女性录取率比男性明显要低，但当我们加上大学中具体学院的数据时，在具体各个学院的数据中，女性录取率反而更高，我们将在后面对相关内容做进一步介绍。多元线性回归中偏回归系数的计算类似于一元线性回归。假设变量Y相对变量X1,X2,…,Xi做线性回归，回归误差项为ε，则有

样本数据集中变量Y的实际值为y，变量Y的预测值为y′，则有整个样本数据集变量Y的实际值与预测值的均方差为

其中上标k表示第k个样本。将式(2.30)分别对r0，r1，…，ri求偏导，并令其为零，则可得到各偏回归系数r0，r1，…，ri。类似于一元线性回归，也可得到多元线性回归各偏回归系数与变量数字特征之间的关系，以二元线性回归为例，其预测变量Y为

分别对式(2.31)两边对变量X和变量Z取协方差，有cov(YX)=cov(r0X)+cov(r1XX)+cov(r2ZX)+cov(εX)cov(YZ)=cov(r0Z)+cov(r1XZ)+cov(r2ZZ)+cov(εZ)联立两个方程，且考虑cov(εX)=0和cov(εZ)=0，计算可得偏相关系数与数字特征关系式：

对于变量Y与变量X（或变量组X）​，无论它们之间是否存在线性相关关系，都可以在样本数据集上应用最小二乘法求得一个线性回归函数。但如果变量Y与变量X（或变量组X）之间根本不存在线性相关关系，则依据该线性回归函数对变量Y进行预测将有较大的误差，这样的线性回归函数没有实际意义。只有当变量Y与变量X（或变量组X）之间存在真正的线性相关关系时，依据该线性回归函数对变量Y进行预测的误差才小，求得的线性回归函数才能用于统计分析预测。因此，在做线性回归之前，应该先检验变量Y与变量X（或变量组X）之间是否存在线性相关关系，该检验通常通过假设检验来实现，具体可见回归分析相关资料，这里不做详细介绍。