Leetcode练习题

高频题参考列表

1、求两数之和

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 的那 两个 整数，并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是，数组中同一个元素不能使用两遍。你可以按任意顺序返回答案。

class Solution(object):
    def twoSum(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[int]
        """
        hashmap={}
        for index,num in enumerate(nums):
            if hashmap.get(target-num) is not None:
                #hashmap.get(target-num) 等价于hashmap[target-num]
                return [index, hashmap.get(target-num)]
            hashmap[num]=index

class Solution(object):
    def twoSum(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[int]
        """
		list1=[]
		for index, num in enumerate(nums):
		    if target-num in list1:
		        return [index, list1.index(target-num)]
		    list1.append(num)

执行结果

执行结果：
通过
显示详情
执行用时：
20 ms
, 在所有 Python 提交中击败了
68.71%
的用户
内存消耗：
13.2 MB
, 在所有 Python 提交中击败了
19.06%
的用户

2、最接近的三数之和

给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有和为 0 且不重复的三元组。
注意：答案中不可以包含重复的三元组。

• 解题思路
  

class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        n=len(nums)
        res=[]
        if(not nums or n<3 or nums[0] > 0):
            return res
        nums.sort()
        for i in range(n):
            if(nums[i]>0):
                return res
            if(i>0 and nums[i]==nums[i-1]):
                """跳过当前循环的剩余语句，然后继续进行下一轮循环,避免重复"""
                continue
            L=i+1
            R=n-1
            while(L<R):
                if(nums[i]+nums[L]+nums[R]==0):
                    res.append([nums[i],nums[L],nums[R]])
                    """下面的两个while为了避免重复的三元组出现"""
                    while(L<R and nums[L]==nums[L+1]):
                        L=L+1
                    while(L<R and nums[R]==nums[R-1]):
                        R=R-1
                    L=L+1
                    R=R-1
                elif(nums[i]+nums[L]+nums[R]>0):
                    """"如果相加大于零，说明最大的数太大，需要左移"""
                    R=R-1
                else:
                    """"如果相加小于零，说明最小的数太小，需要右移"""
                    L=L+1
        return res

• 执行结果
  

3、求众数

给定一个大小为 n 的整数数组，找出其中所有出现超过 ⌊ n/3 ⌋ 次的元素。
进阶：尝试设计时间复杂度为 O(n)、空间复杂度为 O(1)的算法解决此问题。

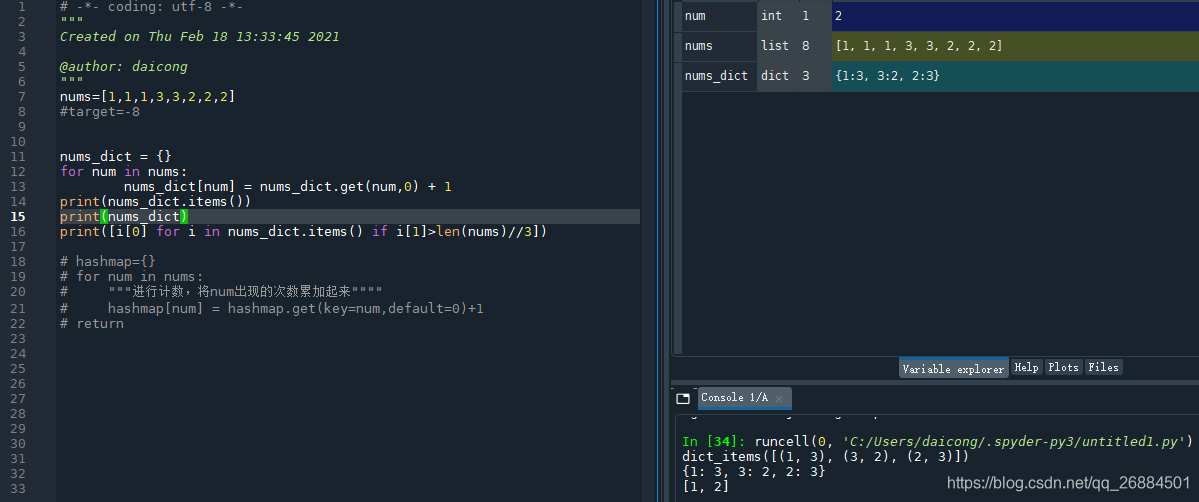
class Solution:
    def majorityElement(self, nums: List[int]) -> List[int]:
        nums_dict = {}
        for num in nums:
                """将num出现的次数以字典的value的形式存储起来"""
                nums_dict[num] = nums_dict.get(num,0) + 1
        """使用列表中的元组将次数大于要求的第一个元素打印出来"""
        return [i[0] for i in nums_dict.items() if i[1]>len(nums)//3]

• 运行结果
  
  拓展

dict.get(key, default=None)
#key -- 字典中要查找的键。
#default -- 如果没有传入key值时，则使用默认key=default=None。
dict.items()
#Python 字典(Dictionary) items() 函数以列表返回可遍历的(键, 值) 元组数组。

• 执行过程
  

总结：灵活的使用dic.get()和dic.item()真是事半功倍！！！

"""
因为有
for key, value in nums_dict.items():
     print([key,value])
所以为了便于理解，也可以写成下面这样，并且运行速度貌似更快了
"""
class Solution:
    def majorityElement(self, nums: List[int]) -> List[int]:
        nums_dict = {}
        for num in nums:
                """将num出现的次数以字典的value的形式存储起来"""
                nums_dict[num] = nums_dict.get(num,0) + 1
        """将字典中value次数大于要求的key打印出来"""
        return [key for key, value in nums_dict.items() if value > len(nums)//3]

4、判断快乐数字

编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」定义为：
对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
如果 可以变为 1，那么这个数就是快乐数。
如果 n 是快乐数就返回 true ；不是，则返回 false 。
示例 1：
输入：19
输出：true
解释：
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1

class Solution:
    def isHappy(self, n: int) -> bool:
        def get_next(n):
            total_sum = 0
            while n > 0 :
                """不断的对10进行整除进行取余操作，一旦n=0时，说明是个位数，跳出循环"""
                n, num2 = divmod(n,10)
                """将取余后的数进行累加，即将每一位的数字进行平方后累加"""
                total_sum += num2**2
            return total_sum
        seen = set()
        """设置seen集合，避免有重复的输出导致死循环"""
        while ( n != 1 and n not in seen):
            seen.add(n)
            """不断的往下迭代，直到满足n=1或者陷入死循环，再跳出循环"""
            n = get_next(n)
        """跳出循环的条件有两个，这里判断时候是因为n=1才跳出的循环"""
        return n == 1

5、求中位数

给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。
请你找出这两个有序数组的中位数，并且要求算法的时间复杂度为 O(log(m + n))。
你可以假设 nums1 和 nums2 不会同时为空

nums=[7,8,9,11,12]
nums2=[7,8,9,11]

nums+=nums2
nums.sort()
if len(nums)%2 ==0:
    print((nums[len(nums)//2]+nums[len(nums)//2-1])/2)
else:
    print(nums[len(nums)//2])
##print(11/2,11//2,11%2) 分别是5.5 ，5 ，1

6、最大连续1的个数 III（1004）

给定一个由若干 0 和 1 组成的数组 A，我们最多可以将 K 个值从 0 变成 1 。
返回仅包含 1 的最长（连续）子数组的长度。
示例
输入：A = [0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1], K = 3
输出：10
解释：
[0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1]
粗体数字从 0 翻转到 1，最长的子数组长度为 10。

参考动画

class Solution:
    def longestOnes(self, A: List[int], K: int) -> int:
        left,right,res,zeroCount = 0,0,0,0
        """设置两个指针，都是从index=0开始，进行右移"""
        while right < len(A):
            if (A[right] == 0):
            """一旦有0就统计下来"""
                zeroCount +=1
            """如果0的个数不满足要求，那么就左移指针，直到满足要求为止"""  
            while (zeroCount > K ):
                if A[left] == 0:
                    zeroCount -=1
                left +=1
             """统计在满足要求的情况下，最大的长度，因为从index=0开始的，所以长度需要+1"""
            res = max(res,right -left +1)
            """不断的右移直至最后一个元素满足条件"""
            right +=1
        return res

滑动窗口模板

《挑战程序设计竞赛》这本书中把滑动窗口叫做「虫取法」，我觉得非常生动形象。因为滑动窗口的两个指针移动的过程和虫子爬动的过程非常像：前脚不动，把后脚移动过来；后脚不动，把前脚向前移动。
我分享一个滑动窗口的模板，能解决大多数的滑动窗口问题：

def findSubArray(nums):
    N = len(nums) # 数组/字符串长度
    left, right = 0, 0 # 双指针，表示当前遍历的区间[left, right]，闭区间
    sums = 0 # 用于统计 子数组/子区间 是否有效，根据题目可能会改成求和/计数
    res = 0 # 保存最大的满足题目要求的 子数组/子串 长度
    while right < N: # 当右边的指针没有搜索到 数组/字符串 的结尾
        sums += nums[right] # 增加当前右边指针的数字/字符的求和/计数
        while 区间[left, right]不符合题意：# 此时需要一直移动左指针，直至找到一个符合题意的区间
            sums -= nums[left] # 移动左指针前需要从counter中减少left位置字符的求和/计数
            left += 1 # 真正的移动左指针，注意不能跟上面一行代码写反
        # 到 while 结束时，我们找到了一个符合题意要求的 子数组/子串
        res = max(res, right - left + 1) # 需要更新结果
        right += 1 # 移动右指针，去探索新的区间
    return res

7、盛最多水的容器(11）

给你 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

我自己做的代码，使用的是暴力破解，一听到暴力就知道，虽然能过了测试用例，但是一定会超时的

class Solution:
    def maxArea(self, nums: List[int]) -> int:
        if (not nums or len(nums) < 2 ):
            return []
        res = -1
        for i in range(len(nums)):
            R = len(nums) -1
            while (i < R ):
                if ((R - i) * min(nums[i],nums[R]) > res):
                    res = (R - i) * min(nums[i],nums[R])
                else:
                    R -= 1    
        return res
        
        """
        上面的if判断代码也可以优化，一行搞定
          while (i < R ):
               res = max((R - i) * min(nums[i],nums[R]),res)
               R -= 1  
        """

代码的改进版本，主要是计算方法上的优化：

参考动画

class Solution:
    def maxArea(self, nums: List[int]) -> int:
        res,left,right = 0,0,len(nums)-1
        while left < right:
            """使用高度来进行对比，如果高度高的话，则高的不动，使用低的计算面积，如果左边低，则左移"""
            if nums[left] < nums[right]:
                """更新最大面积"""
                res = max(res,nums[left]*(right - left))
                left += 1
            else:
                """右边低则右移"""
                res = max(res,nums[right]*(right - left))
                right -= 1
        return res

8、删除排序数组中的重复项

给定一个排序数组，你需要在 原地 删除重复出现的元素，使得每个元素只出现一次，返回移除后数组的新长度。
不要使用额外的数组空间，你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。

• 这个题首先删除重复的元素指的是相邻的元素不能重复，其次输出结果应该是列表而非长度。虽然返回值是长度，在测试时,结果输出的是列表，因为根据你的函数返回的长度, 它会打印出数组中该长度范围内的所有元素
• 使用双指针，行云流水，万能解法

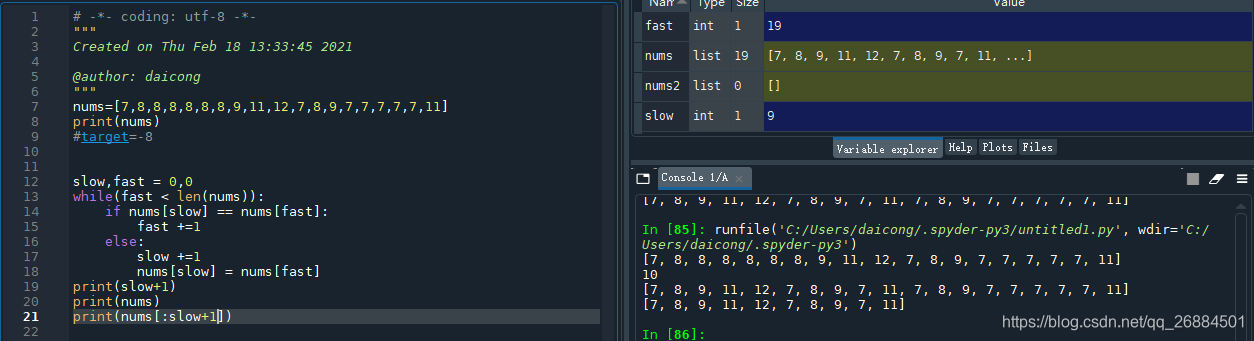
class Solution:
    def removeDuplicates(self, nums: List[int]) -> int:
        slow,fast = 0,0
        while(fast < len(nums)):
            if nums[slow] == nums[fast]:
                fast +=1
            else:
                slow +=1
                nums[slow] = nums[fast]
        return slow+1

9、搜索旋转排序数组

升序排列的整数数组 nums 在预先未知的某个点上进行了旋转（例如，[0,1,2,4,5,6,7] 经旋转后可能变为 [4,5,6,7,0,1,2] ）。
请你在数组中搜索 target ，如果数组中存在这个目标值，则返回它的索引，否则返回 -1 。

• 解题思路

数组从任意位置劈开后，至少有一半是有序的。
基于这个事实。我们可以先找到哪一段是有序的 (只要判断端点即可)，然后看 target 在不在这一段里，如果在，那么就把另一半丢弃。如果不在，那么就把这一段丢弃。

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        if not nums:
            return -1
        left = 0
        right = len(nums) - 1
        while left <= right:
            mid = (left + right) // 2
            if nums[mid] == target:
                return mid
            
            # 左半段有序
            if nums[mid] >= nums[left]:
                if nums[left] <= target <= nums[mid]:
                    right = mid - 1
                else:
                    left = mid + 1
            # 右半段有序
            else:
                if nums[mid] <= target <= nums[right]:
                    left = mid + 1
                else:
                    right = mid - 1
        return -1

貌似被算法得的复杂度限制了，使用下面的代码也能够通过测试

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        for index, num in enumerate(nums):
            if target == num:
                return index
        return -1

10、螺旋矩阵(54)

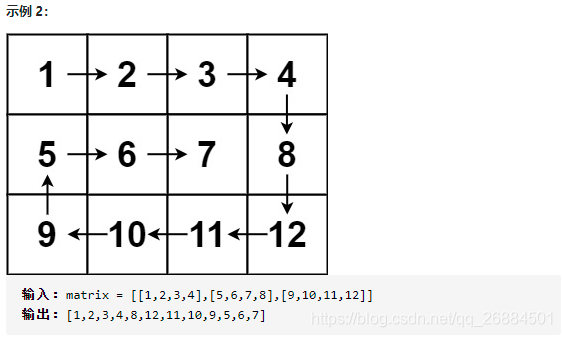
class Solution(object):
    def spiralOrder(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: List[int]
        row start row end
        column start column end
        """
        rs, cs = 0, 0       # 设置行的起始位置rs=0和列的起始位置cs=0
        re, ce = len(matrix), len(matrix[0])    # 设置行的结束位置re=n和列的结束位置ce=n
        res = []    # 存放结果的数组
        while rs < re and cs < ce:
            """如果非最后一行并且非最后一列，则则执行循环"""
            
            for i in range(cs,ce):            # 遍历首行 
                res.append(matrix[rs][i])
            rs += 1
            if rs>=re:
                """如果是最后一行，那么跳出循环"""
                break
            
            for j in range(rs,re):            # 遍历尾列
                res.append(matrix[j][ce-1])
            ce -= 1
            if cs>=ce:
                """如果是最后一列，那么跳出循环"""
                break
            
            for i in range(ce-1,cs-1,-1):     # 遍历尾行
                """因为不包括最后一行，所有ce-1,因为想取到第一行，所以cs-1"""
                res.append(matrix[re-1][i])
            re -= 1
            if rs>=re:
                """如果是最后一行，那么跳出循环"""
                break
            
            for j in range(re-1,rs-1,-1):     # 遍历首列
                res.append(matrix[j][cs])
            cs += 1
            if cs>=ce:
                """如果是最后一列，那么跳出循环"""
                break
        return res

11、螺旋矩阵II

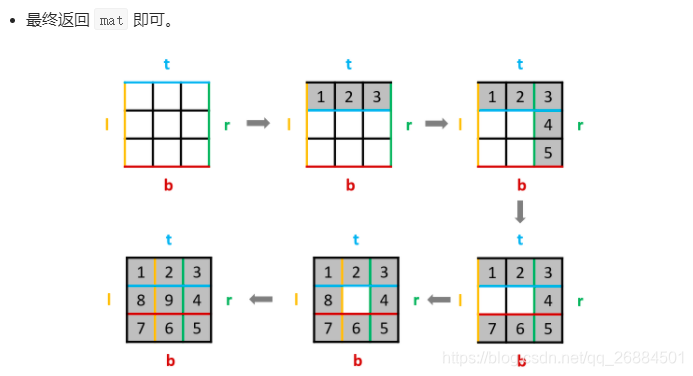
• 本想着这个题和上面的题一样，只不过输入是我们自己自定义，仔细研究才发现还是不一样的，这一题是按照顺时针的顺序，将数一个一个的放进去，去生成这个矩阵。实际上还是可以用到上面的遍历方式，将数字一个一个的放进去

for j in range(n):
    matrix = [[i+n*j for i in range(1,n+1)] for j in range(n)]
#n=3
#输出[[1, 2, 3], [4, 5, 6], [7, 8, 9]]

• 解法

class Solution:
    def generateMatrix(self, n: int) -> List[List[int]]:
        matrix  = [[0 for i in range(n)] for _ in range(n)]
        rs, cs = 0, 0
        re, ce = n, n
        num = 1
        end = n * n
        
        while num <= end:
        	"""首行"""
            for i in range(cs,ce):
                matrix[rs][i] = num
                num += 1
            rs += 1
        	"""尾列"""
            for i in range(rs,re):
                matrix[i][ce-1] = num
                num += 1
            ce -= 1
         	"""尾行"""
            for i in range(ce-1,cs-1,-1):
                matrix[re-1][i] = num
                num += 1
            re -= 1
        	"""首列"""
            for i in range(re-1,rs-1,-1):
                matrix[i][cs] = num
                num += 1
            cs += 1
        return matrix

12、螺旋矩阵III

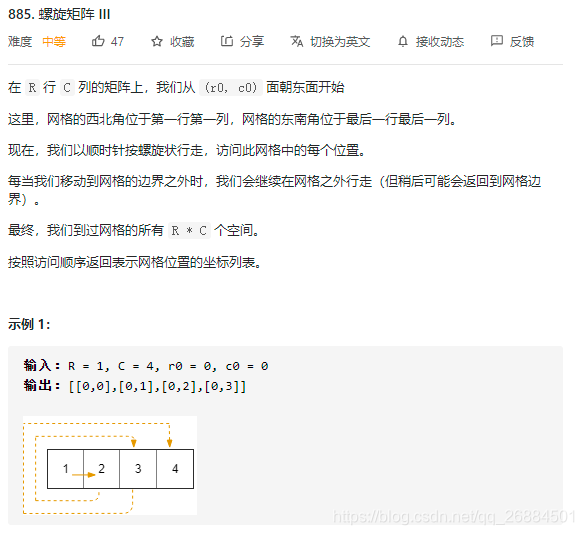
class Solution:
    def spiralMatrixIII(self, R: int, C: int, r0: int, c0: int) -> List[List[int]]:
        ans = []
        di, dj, step = 0, 1, 0
        # 从内往外走，初始值走一步就要转
        while len(ans) < R*C:
            for s in range(step//2+1):
                if 0<=r0<R and 0<=c0<C:
                    ans.append((r0, c0))
                r0, c0 = r0+di, c0+dj

            di, dj, step = dj, -di, step+1
        return ans

13、环形链表

判断链表中是否存在环
使用的是快慢指针的思想，解释的极其详尽
参考1为什么使用快慢指针
参考2为什么步长为二

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def hasCycle(self, head: ListNode) -> bool:
        """如果链表为空挥或者只有一个元素，就无法形成环"""
        if not head or not head.next: return False
        slow = head
        fast = head.next

        while slow != fast:
            """如果慢指针和快指针始终不相等，那么说明是没有环的"""
            if not fast or not fast.next:
                """如果遍历到底了，那么就没有环"""
                return False
            """慢指针每次走一步，快指针每次走两步"""
            slow = slow.next 
            fast = fast.next.next
        """跳出while循环说明是有环的"""
        return True

13、环形数组循环

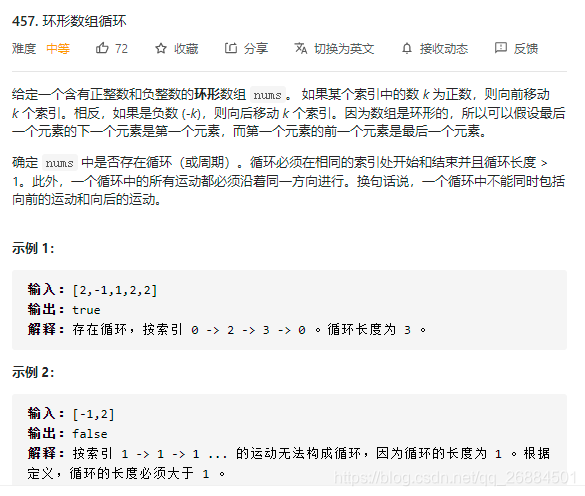
思路：快慢指针
通过快慢指针找到是否存在环
时间复杂度为O(n)，空间复杂度为O(1)
思路是：
对于查找数组或链表中有没有环的问题，多可以朝快慢指针的方向去想，本题也不例外。基本思想是快慢指针。还有一些小细节和技巧的东西需要考虑在内。
1）数组长度为0时，认为无环。
2）快慢指针的思想是慢指针走一步，快指针走两步，若他俩相遇肯定是在环中的某一个节点上相遇，则证明存在环。
3）假设位置i的元素是环中的一点，通过快慢指针的思想，假定慢指针为j快指针为k，那么一定会有j==k的时候。问题是位置i可能不是环中的一个节点。鉴于此肯定是要遍历全部的节点的。for(i = 0; i < nums.length;++i>)对于这样的i都要试一试是否是环中的一个节点，若是则return true，否则则return false；如果这样的话，肯定做不到时间复杂度是O(n)的程度，要稍微“剪下枝”。
4）根据提示，nums中所有元素都不可能是0。这是剪枝可以进行的关键。另一个原则是如果存在环，那么环中的所有数字的符号都必须是一致，否则不满足题意。这时我们认为本链条不处于环上。然后将节点i到当前位置的所有元素置0，以标记这些节点都不在环上。
5）另一点是：当某节点j指向已经确定不在环中的节点时，就不必继续走下去了，节点j肯定也不在环上。
6）当循环长度为1是，也是不存在环的，比如[8,2]这个数组，从任意位置开始都指向它自己。我们认为他是无环的。
基本思路说完了，不知道读者懂没懂^_。
重述下无环的判定依据：
1）当快慢指针指向的新节点发现和上一个节点符号不一致。
2）当快慢指针指向的位置不变时。
3）快慢指针指向了不可能是环中节点的节点(该节点位置已经置0的节点)时。

class Solution:
    def circularArrayLoop(self, nums: List[int]) -> bool:
        n = len(nums)
        # x的下一个位置
        nxt = lambda x: (x + nums[x]) % n

        for i in range(n):
            if nums[i] == 0: continue
            slow = i
            fast = nxt(i)
            # 快慢指针
            """符号相同保证是同一个方向移动"""
            while nums[slow] * nums[fast] > 0 and nums[fast] * nums[nxt(fast)] > 0:
                """快指针每次走两步，如果快慢指针相等，说明有环"""
                if slow == fast:
                    """如果是自身环，那么退出循环"""
                    if slow == nxt(slow):
                        break
                    else:
                        return True
                """更新状态，快指针每次走两步"""
                slow = nxt(slow)
                fast = nxt(nxt(fast))
            # 访问过的置0
            """如果上面那轮没有return，说明上面遍历过的元素都不可能成环，为避免再次遍历陷入无效查找，故将查找过的元素置零，再次遍历时直接跳过"""
            while nums[i] > 0:
                """先找到下一个元素的index"""
                tmp = nxt(i)
                """将当前的元素置零"""
                nums[i] = 0
                """向下走一步"""
                i = tmp
        return False

"""
使用的快慢指针，初始列表中的元素不可能有0
1、首先判断方向一致
2、有环的情况下，判断是否是自身环
3、没环的情况下，将遍历过的元素置零避免重复遍历
"""

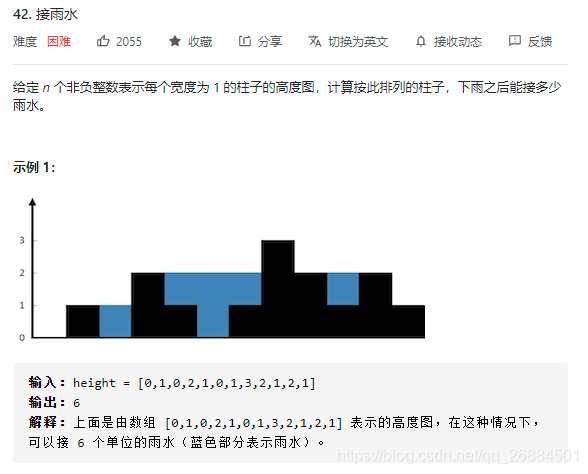
14、接雨水(42)

• 暴力法：

时间复杂度：O(N^2)。
空间复杂度：O(1)。

class Solution:
    def trap(self, height: List[int]) -> int:
        if len(height) <= 2:
            return 0
        res = 0
        for i in range(1, len(height)-1):
            left_max = max(height[:i+1])
            right_max = max(height[i:])
            res += (min(left_max, right_max) - height[i])
        return res

• 双指针法：

时间复杂度：O(N)。
空间复杂度：O(1)。

class Solution:
    def trap(self, height: List[int]) -> int:
        if len(height) <= 2:
            return 0
        res = 0
        left, right = 0, len(height) - 1
        left_max, right_max = height[0], height[-1]
        while left <= right:
            left_max = max(left_max, height[left])
            right_max = max(right_max, height[right])
            if left_max < right_max:
                res += left_max - height[left]
                left += 1
            else:
                res += right_max - height[right]
                right -= 1
        return res

15、接雨水II(407)

使用小顶堆的方式

• 这个视频很清晰：https://www.youtube.com/watch?v=cJayBq38VYw

from heapq import *
class Solution:
    def trapRainWater(self, heightMap: List[List[int]]) -> int:
        """
        水从高出往低处流，某个位置储水量取决于四周最低高度，从最外层向里层包抄，用小顶堆动态找到未访问位置最小的高度
        """
        if not heightMap:return 0
        imax = float('-inf')
        ans = 0
        heap = []
        visited = set()
        row = len(heightMap)
        col = len(heightMap[0])
        # 将最外层放入小顶堆
        # 第一行和最后一行
        for j in range(col):
            # 将该位置的高度、横纵坐标插入堆
            heappush(heap, [heightMap[0][j], 0, j])  
            heappush(heap, [heightMap[row - 1][j], row - 1, j])
            visited.add((0, j))
            visited.add((row - 1, j))
        # 第一列和最后一列
        for i in range(row):
            heappush(heap, [heightMap[i][0], i, 0])
            heappush(heap, [heightMap[i][col - 1], i, col - 1])
            visited.add((i, 0))
            visited.add((i, col - 1))
        while heap:
            h, i, j = heappop(heap)
            # 之前最低高度的四周已经探索过了，所以要更新为次低高度开始探索
            imax = max(imax, h)  
            # 从堆顶元素出发，探索四周储水位置
            for x, y in [[0, 1], [1, 0], [0, -1], [-1, 0]]:
                tmp_x = x + i 
                tmp_y = y + j
                # 是否到达边界
                if tmp_x < 0 or tmp_y < 0 or tmp_x >= row or tmp_y >= col or (tmp_x, tmp_y) in visited:
                    continue
                visited.add((tmp_x, tmp_y))
                if heightMap[tmp_x][tmp_y] < imax:
                    ans += imax - heightMap[tmp_x][tmp_y]
                heappush(heap, [heightMap[tmp_x][tmp_y], tmp_x, tmp_y])
        return ans

16、最长回文子串

参考

class Solution:
    def longestPalindrome(self, s: str) -> str:
        n = len(s)
        dp = [[False] * n for _ in range(n)]
        ans = ""
        # 枚举子串的长度 l+1
        for l in range(n):
            # 枚举子串的起始位置 i，这样可以通过 j=i+l 得到子串的结束位置
            for i in range(n):
                j = i + l
                if j >= len(s):
                    break
                if l == 0:
                    dp[i][j] = True
                elif l == 1:
                    dp[i][j] = (s[i] == s[j])
                else:
                    dp[i][j] = (dp[i + 1][j - 1] and s[i] == s[j])
                if dp[i][j] and l + 1 > len(ans):
                    ans = s[i:j+1]
        return ans

上面的代码没问题太，就是运行超时，需要进行优化

• 优化版本1

class Solution:
    def expandAroundCenter(self, s, left, right):
        while left >= 0 and right < len(s) and s[left] == s[right]:
            left -= 1
            right += 1
        return left + 1, right - 1

    def longestPalindrome(self, s: str) -> str:
        start, end = 0, 0
        for i in range(len(s)):
            left1, right1 = self.expandAroundCenter(s, i, i)
            left2, right2 = self.expandAroundCenter(s, i, i + 1)
            if right1 - left1 > end - start:
                start, end = left1, right1
            if right2 - left2 > end - start:
                start, end = left2, right2
        return s[start: end + 1]

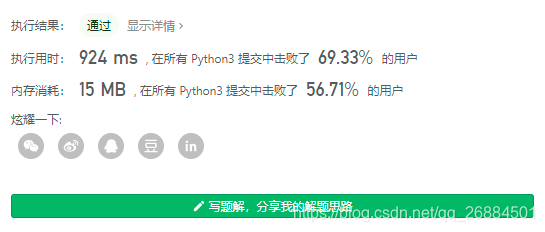
• 优化版本2

class Solution:
    def expand(self, s, left, right):
        while left >= 0 and right < len(s) and s[left] == s[right]:
            left -= 1
            right += 1
        return (right - left - 2) // 2

    def longestPalindrome(self, s: str) -> str:
        end, start = -1, 0
        s = '#' + '#'.join(list(s)) + '#'
        arm_len = []
        right = -1
        j = -1
        for i in range(len(s)):
            if right >= i:
                i_sym = 2 * j - i
                min_arm_len = min(arm_len[i_sym], right - i)
                cur_arm_len = self.expand(s, i - min_arm_len, i + min_arm_len)
            else:
                cur_arm_len = self.expand(s, i, i)
            arm_len.append(cur_arm_len)
            if i + cur_arm_len > right:
                j = i
                right = i + cur_arm_len
            if 2 * cur_arm_len + 1 > end - start:
                start = i - cur_arm_len
                end = i + cur_arm_len
        return s[start+1:end+1:2]

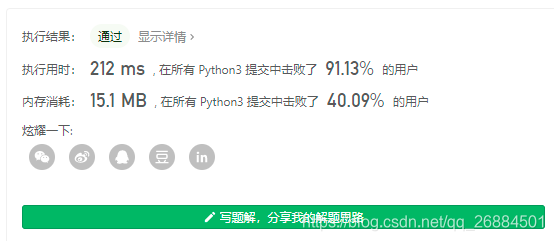
17、买卖股票的最佳时机

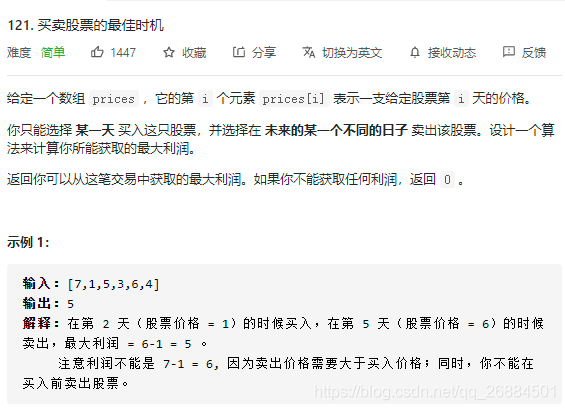
class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        """定义最小的价格为无穷大"""
        minprice = float("inf")
        res = 0
        for price in prices:
            """找出最小的价格"""
            minprice = min(minprice, price)
            """保存最大的利润差"""
            res = max(res,price-minprice)
        return res

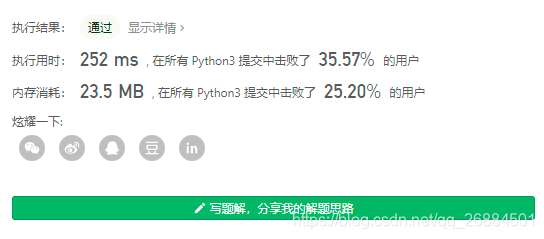
• 使用动态规划，参考
• 

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        n = len(prices)
        if n == 0: return 0 # 边界条件
        dp = [0] * n
        minprice = prices[0] 

        for i in range(1, n):
            minprice = min(minprice, prices[i])
            """将临时最优解决存储在dp中，最后返回最优解"""
            dp[i] = max(dp[i - 1], prices[i] - minprice)

        return dp[-1]

18、买卖股票的最佳时机 II

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        """贪心算法"""
        res = 0
        for i in range(1,len(prices)):
            """只要今天比昨天高，就立即卖出获得收益"""
            if prices[i] > prices[i-1]:
                res += prices[i] - prices[i-1]
        return res

使用动态规划

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        """动态规划算法，i表示天，0表示手里没股票持有收益，1表示有股票，当天卖出的话得到截至当天的总收益"""
        n = len(prices)
        dp = [[0 for _ in range(2)] for _ in range(n)]
        """
        第0天之前收益肯定是0，所以第0天：
        如果手里面没有股票，那么收益为0；
        如果有股票，说明是当天买的，当天卖出的话获得截至当天的总收益-prices[0]
        """
        dp[0][0] = 0
        dp[0][1] = -prices[0]
        for i in range(1,n):
            """
            今天手中没有股票：
            1、前一天手中也没有股票；
            2、前一天手中有股票，今天卖掉了,所以利润加上销售所得prices[i]
            """
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i])
            """
            今天手中有股票：
            1、前一天手中也股票；
            2、前一天手中没有股票，今天买了，所以利润减去开销prices[i]
            """
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i])
        """返回最后一天手里没有股票的最大收益。截至前一天的利润一定是最大化的，如果考虑今天手中股票说明今天买的，还要减去卖股的钱，利润就会变少"""
        return dp[n - 1][0]

19、约瑟夫环

参考

class Solution:

    def lastRemaining(self, n: int, m: int) -> int:
        if n == 1:
            return 0

        last = 0
        for i in range(2, n + 1):
            last = (last + m) % i

        return last

n = 5
m = 3
s = Solution()
print(s.lastRemaining(n, m))

20、二叉树最大深度

参考

class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if not root: return 0
        return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1

21、二叉树非递归中序遍历

参考

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        TreeNode *predecessor = nullptr;

        while (root != nullptr) {
            if (root->left != nullptr) {
                // predecessor 节点就是当前 root 节点向左走一步，然后一直向右走至无法走为止
                predecessor = root->left;
                while (predecessor->right != nullptr && predecessor->right != root) {
                    predecessor = predecessor->right;
                }
                
                // 让 predecessor 的右指针指向 root，继续遍历左子树
                if (predecessor->right == nullptr) {
                    predecessor->right = root;
                    root = root->left;
                }
                // 说明左子树已经访问完了，我们需要断开链接
                else {
                    res.push_back(root->val);
                    predecessor->right = nullptr;
                    root = root->right;
                }
            }
            // 如果没有左孩子，则直接访问右孩子
            else {
                res.push_back(root->val);
                root = root->right;
            }
        }
        return res;
    }
};

22、二叉树最大通路

参考

class TreeNode {

    int val;
    TreeNode left;
    TreeNode right;

    public TreeNode(int val) {
        this.val = val;
    }
}

递归求解

class Solution {

    public int maxHeight(TreeNode root) {
        if (root == null) {
            return 0;
        }
        return maxChildHeight(root.left) + maxChildHeight(root.right);
    }

    public int maxChildHeight(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftHeight = maxChildHeight(root.left);
        int rightHeight = maxChildHeight(root.right);
        return Math.max(leftHeight, rightHeight) + 1;
    }
}

迭代求解

public class Solution {

    public int maxHeight(TreeNode root) {
        if (root == null) {
            return 0;
        }
        return maxChildHeight(root.left) + maxChildHeight(root.right);
    }

    public int maxChildHeight(TreeNode root) {
        int height = 0;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);

        while (!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode node = queue.poll();
                height++;
                if (node.left != null) {
                    queue.add(node.left);
                }
                if (node.right != null) {
                    queue.add(node.right);
                }
            }
        }
        return height;
    }
}

23、牛顿法求解方程

通过上面的解释就可以对方程进行求解了，比如下面这道题

相当于是求解f(x) = x**2 -m使得f(x) =0的解，当然这里的f(x)只能无限的趋近于零，因为要保留小数点的后4位，我们可以令f(x)=1e-5
f’(x) = 2x,带入上面的泰勒展开式的求解方程中，可以得到x=x0/2-(x0**2-m)/2*x0

def newton(m):
    x0 = m/2 #初始点，也可以是别的值
    x1 = x0/2 + m/(x0*2)
    while abs(x1-x0)>1e-5:
        x0 = x1
        x1 = x0/2 + m/(x0*2)
    return x1
#输出精确到小数点后四位
print('%.4f'%newton(2))

"""
1.4142
"""

同理我们可以得到算术立方根的求解方法

f(x) = x**3 -m
f’(x) = 3x**2
带入公式可得x1 = 2*x0/3 + m/(3*x0**2)

代码实现：

def three_sqr(m):
    x0 = m/2
    x1 = 2*x0/3 + m/(3*x0**2)
    while abs(x1-x0) > 1e-5:
        x0 = x1
        x1 = 2*x0/3 + m/(3*x0**2)
    return x1
print( '%.4f'%three_sqr(5))
print(1.71**3)

"""
1.7100
5.000210999999999
"""

同理可得算术q阶根

def q_sqr(m,q):
    x0 = m/2
    x1 = x0 - (x0**q-m)/(q*x0**(q-1))
    while abs(x1-x0) > 1e-5:
        x0 = x1
        x1 = x0 - (x0**q-m)/(q*x0**(q-1))
    return x1
print( '%.4f'%q_sqr(8,4))
print(1.6818**4)

"""
1.6818
8.000136417057536
"""

利用魔法数字求解

float Q_rsqrt( float number )
{
	long i;
	float x2, y;
	const float threehalfs = 1.5F;
 
	x2 = number * 0.5F;
	y  = number;
	i  = * ( long * ) &y;						// evil floating point bit level hacking
	i  = 0x5f3759df - ( i >> 1 );               // what the fuck?
	y  = * ( float * ) &i;
	y  = y * ( threehalfs - ( x2 * y * y ) );   // 1st iteration
//	y  = y * ( threehalfs - ( x2 * y * y ) );   // 2nd iteration, this can be removed
 
#ifndef Q3_VM
#ifdef __linux__
	assert( !isnan(y) ); // bk010122 - FPE?
#endif
#endif
	return y;
}

加速版本

float InvSqrt(float x)
{
    float xhalf = 0.5f * x;
    int i = *(int *)&x;
    i = 0x5f3759df - (i>>1);
    x = *(float *)&i;
    x = x * (1.5f - xhalf * x * x);
    return x;
}

200. 岛屿数量
33. 搜索旋转排序数组

24. 图像渲染

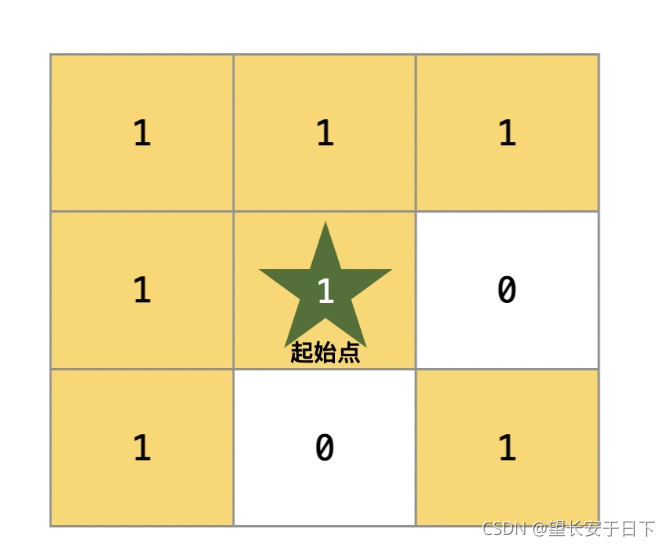
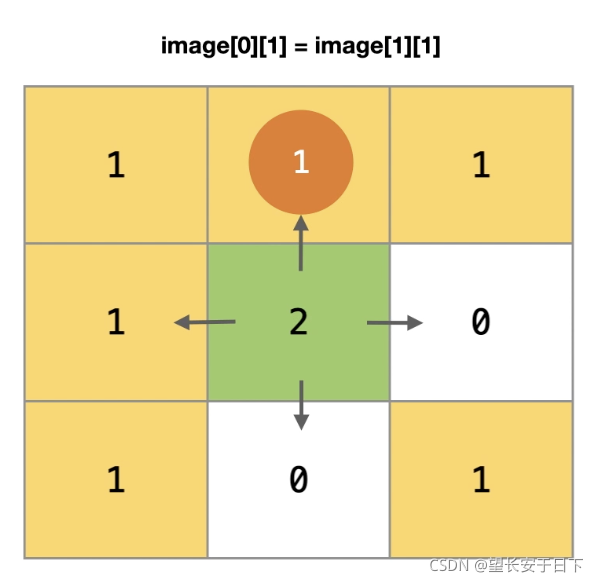
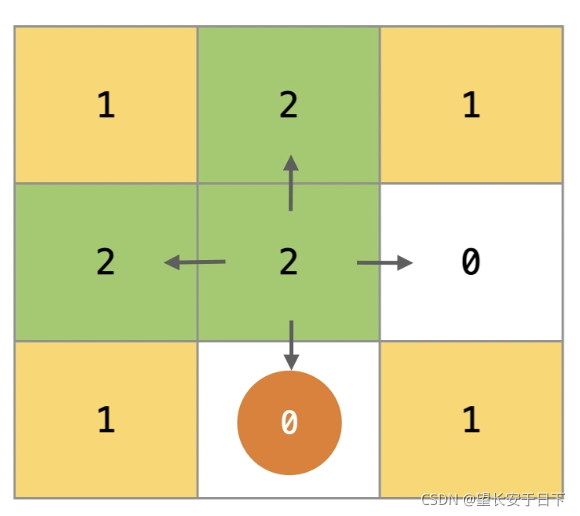
class Solution:#使用递归
    def floodFill(self, image: List[List[int]], sr: int, sc: int, newColor: int) -> List[List[int]]:
        if image[sr][sc] != newColor:
            old,image[sr][sc] = image[sr][sc], newColor
            for i,j in zip((sr,sr+1,sr,sr-1),(sc+1,sc,sc-1,sc)):
                if 0 <= i < len(image) and 0 <= j < len(image[0]) and image[i][j] == old:#边界条件，不能超出长和宽，并且还要颜色不一样
                    self.floodFill(image,i,j,newColor)
        return image

26. 最大岛屿

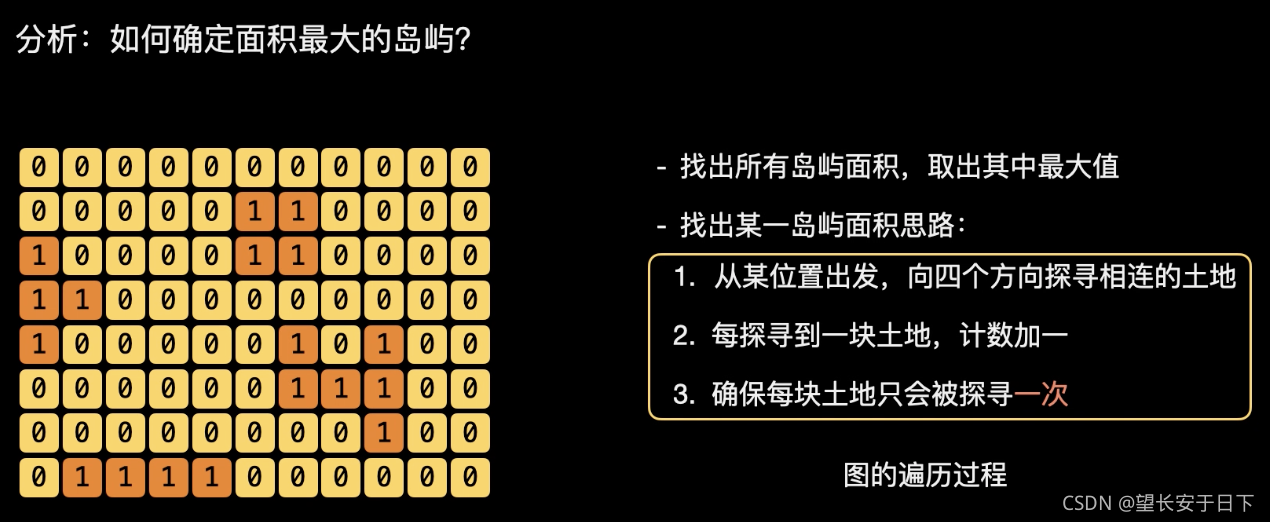
"""深度优先+栈"""
"""
方法一通过函数的调用来表示接下来想要遍历哪些土地，让下一层函数来访问这些土地。而方法二把接下来想要遍历的土地放在栈里，然后在取出这些土地的时候访问它们。
访问每一片土地时，我们将对围绕它四个方向进行探索，找到还未访问的土地，加入到栈 stack 中；
另外，只要栈 stack 不为空，就说明我们还有土地待访问，那么就从栈中取出一个元素并访问。
"""
class Solution:
    def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
        ans = 0
        for i, l in enumerate(grid):
            for j, n in enumerate(l):
                cur = 0
                stack = [(i, j)]
                while stack:
                    cur_i, cur_j = stack.pop()
                    if cur_i < 0 or cur_j < 0 or cur_i == len(grid) or cur_j == len(grid[0]) or grid[cur_i][cur_j] != 1:
                        continue
                    cur += 1
                    grid[cur_i][cur_j] = 0
                    for di, dj in [[0, 1], [0, -1], [1, 0], [-1, 0]]:
                        next_i, next_j = cur_i + di, cur_j + dj
                        stack.append((next_i, next_j))
                ans = max(ans, cur)
        return ans

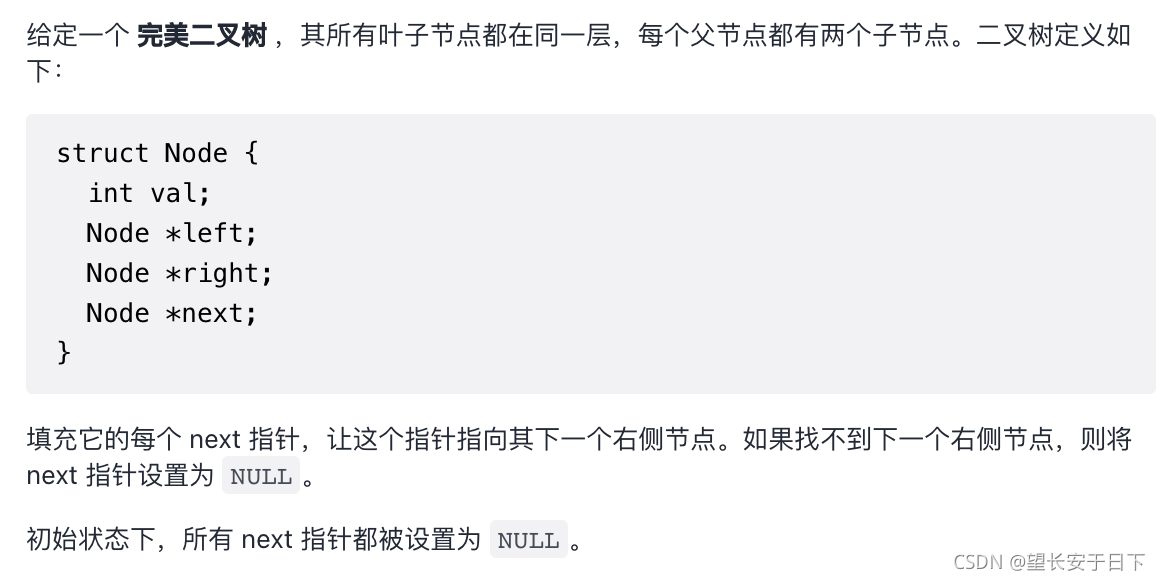
27.完美二叉树

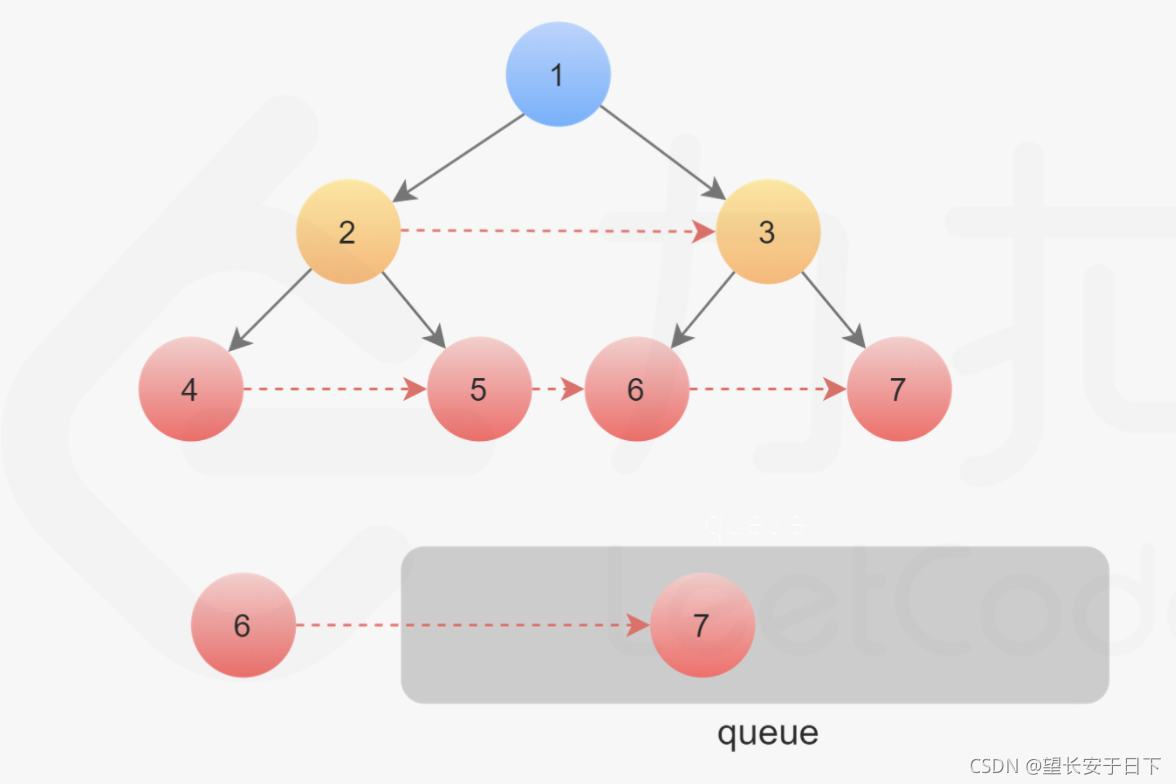
28. 矩阵