1.Dijkstra算法介绍
Dijkstra是解决从一个顶点到其余各顶点的最短路径算法,解决的是有向图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
2.算法实现
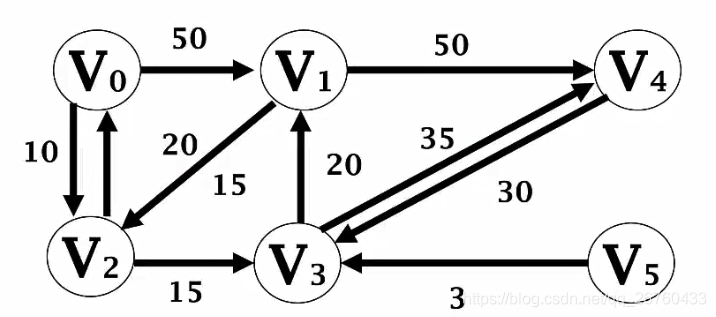
例如求V0到达各个节点的最短路径,我这里用的邻接表存储图,用到了STL里的优先队列,而且要进行运算符重载。
贴代码
#include<vector>
#include<iostream>
#include<queue>
using namespace std;
class road
{
public:
int end; //路径到达的终点
int weight; //路径的权重
};
class Graph
{
public:
int v; //顶点个数
int *mark; //标记,如果已访问标记为1,否则为0
vector<road> *adj; //邻接表
Graph(int n); //构造函数
~Graph(); //析构函数
void addEdge(int b,int e,int w); //添加边
};
Graph::Graph(int n) //构造函数
{
v=n; //顶点数
mark=new int[n];
adj=new vector<road>[n];
for(int i=0;i<n;i++) //所有顶点标记为0
{
mark[i]=0;
}
}
Graph::~Graph() //析构函数
{
delete [] adj;
delete [] mark;
}
void Graph::addEdge(int b,int e,int w) //添加一条边
{
road r;
r.end=e;
r.weight=w;
adj[b].push_back(r);
}
class Dist //Dist类,用于保存最短路径信息
{
public:
int index; //节点的索引值
int length; //到达改节点的长度
int pre; //节点的前驱
friend bool operator<(const Dist & a,const Dist &b) //重载 <
{
return a.length>b.length;
}
};
void Dijkstra(Graph & g,int s) //s是起点
{
Dist *D=new Dist[g.v];
for(int i=0;i<g.v;i++) //Dist初始化
{
D[i].index=i;
D[i].length=1<<30;
D[i].pre=s;
}
D[s].length=0; //到达起始节点路径为0
priority_queue<Dist> aqueue; //优先队列,找最短路径
aqueue.push(D[s]); //入队
for(int i=0;i<g.v;i++)
{
Dist d;
bool FOUND=false;
while(!aqueue.empty())
{
d=aqueue.top(); //获得到s路径长度最小的节点
aqueue.pop();
if(g.mark[d.index]==0) //找到并跳出循环
{
FOUND=true;
break;
}
}
if(!FOUND) //若没有符合条件的最短路径则跳出本次循环
break;
int node=d.index;
g.mark[node]=1; //标记为1
vector<road>::iterator ii=g.adj[node].begin(); //刷新最短路径
for(;ii!=g.adj[node].end();ii++)
{
if( D[ii->end].length > D[node].length+ ii->weight )
{
D[ii->end].length = D[node].length+ ii->weight;
D[ii->end].pre = node;
aqueue.push(D[ii->end]);
}
}
}
for(int i=0;i<g.v;i++)
{
if(D[i].length==1<<30)
{
cout<<"无法到达节点:"<<D[i].index<<endl;
continue;
}
cout<<"到达节点:"<<D[i].index<<" 最短路径为:"<<D[i].length<<endl;
}
}
int main()
{
Graph g(6);
g.addEdge(0,1,50);
g.addEdge(0,2,10);
g.addEdge(1,2,15);
g.addEdge(1,4,50);
g.addEdge(2,0,20);
g.addEdge(2,3,15);
g.addEdge(3,4,35);
g.addEdge(3,1,20);
g.addEdge(4,3,30);
g.addEdge(5,3,3);
Dijkstra(g,0);
return 0;
}
运行结果
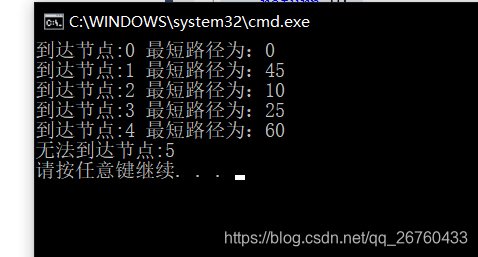





















 358
358

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








