js中0.1+0.2！=0.3

最新推荐文章于 2025-08-12 09:49:09 发布

原创最新推荐文章于 2025-08-12 09:49:09 发布 · 1.1k 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#javascript #java #servlet

前端专栏收录该内容

136 篇文章

订阅专栏

博客主要解释了JS中以0开头数字的二进制隐式转换规则，通过将0.1和0.2转换为二进制无限循环数，相加后再转换为十进制，得出结果为0.3000000000000004，因JS浮点型数据有效保留17位，所以出现该结果，还提及类似的0.1+0.7情况。

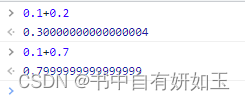
这是为什么呢？

答：js中以0开头的数字都会以2进制隐式转换，转换规则如下

以小数本身乘以2,取整数部分表示位数，然后取小数部分重新计算，循环往复，知道小数部分乘以2的结果为0；

按照上面的结论推算

0.1 ==》 0.0 0011 0011 0011 0011... 无限循环

0.1*2=0.2 0.6*2=1.2

0.2*2=0.4 0.2*2=0.4

0.4*2=0.8 0.4*2=0.8

0.4*2=1.6 0.4*2=1.6

同理可以得到0.2的二进制数为

0.2 ==》 0.0011 0011 0011 0011...无限循环

所以 0.1+0.2 ==

0.0 0011 0011 0011 0011... 无限循环

+ 0.0011 0011 0011 0011...无限循环

----------------------------------------------------------

= 0.0100 1100 1100 1100...无限循环

最后将 0.0100 1100 1100 1100...无限循环转化为10进制就是 0.30000000000000044408958

而js中浮点型数据有效保留位数是17位所以才有了上图中的 0.3000000000000004。

与之类似的还要0.1+0.7，大家现在明白了吗？

确定要放弃本次机会？

福利倒计时

: :

立减 ¥

普通VIP年卡可用

立即使用

书中自有妍如玉

关注关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
分享

复制链接

分享到 QQ

分享到新浪微博

扫一扫
举报

举报

专栏目录

javascript 0.1+0.2!==0.3

且听风吟的博客

08-05

723

一个例子： 0.1+0.2 结果： 0.30000000000000004

js浮点数运算精度问题：0.1+0.2≠0.3

qq_39437900的博客

05-18

1627

js浮点数运算精度问题：0.1+0.2≠0.3问题概述分析问题基础知识二进制科学记数法十进制小数转二进制核心问题IEEE 754简介双精确度（64位）储存浮点数运算对阶尾数求和规格化和舍入解决问题一、toFixed()二、Number.EPSILON三、转化成整数总结问题概述在js运算中0.1+0.2运算结果为0.30000000000000004，即0.1+0.2≠0.3 console.log(0.1 + 0.2) //0.30000000000000004 console.log(0.1 + 0

参与评论您还未登录，请先登录后发表或查看评论

js 0.1+0.2=0.3

qq_34941404的博客

08-29

355

【代码】js 0.1+0.2=0.3。

js解决0.1+0.2==0.3的问题的几种方法

热门推荐

weixin_34018202的博客

02-21

1万+

js解决0.1+0.2==0.3的问题的几种方法 JavaScript有7种基本类型分别是: Undefined, Null, Boolean, String, Number, Symbol, Object. 对于JS中的Number类型, 不区分整数和浮点数, 浮点数的精度远远不如整数, 首先先看一下为什么会出现这个问题, 根据双精度浮...

JavaScript中 0.1+0.2==0.3 是否正确（附相加的计算过程）

xawjz的博客

08-19

1675

先上结论：0.1+0.2 == 0.3 在JavaScript中是错误的。原因系统学习过计算机基础理论知识的都应该知道，计算机中的数据是以二进制存储的。相关的，我们想要比较两个数的大小，计算机又是怎样实现的呢，总不可能是直接像人脑一样经过看似简单实则复杂的方式进行对比。计算机的思考方式是非常简单，非0即1（没别的意思 /狗头）。首先来看Javascript是如何存储小数的 JavaScirpt 使用 Number 类型来表示数字（整数或...

精选资源

为什么JavaScript中0.1 + 0.2 != 0.3

01-21

涉及面试题：为什么 0.1 + 0.2 != 0.3？如何解决这个问题？原因，因为 JS 采用 IEEE 754双精度版本（64位），并且只要采用 IEEE 754的语言都有该问题我们都知道计算机是通过二进制来存储东西的，那么 0.1 在二进制...

解决JavaScript中0.1+0.2不等于0.3问题

10-17

这就是为什么在JavaScript中`0.1 + 0.2`不等于`0.3`的原因。为了正确地比较两个浮点数，我们需要引入一个误差范围，也就是所谓的“机器精度”。在JavaScript中，这个精度值可以通过`Number.EPSILON`属性获取，其值...

精选资源

js代码-面试题---0.1 +0.2 为啥不精确等于0.3

07-14

在JavaScript中，0.1 + 0.2 不精确等于 0.3 是一个常见的面试问题，涉及到浮点数在计算机中的表示与计算。这个问题源于浮点数在二进制系统下的表示方式以及IEEE 754标准。下面将详细解释这一现象的原因以及相关的...

揭秘JS浮点数陷阱：为何0.1+0.2≠0.3？

技术分享

07-01

1840

本文深入解析JavaScript中浮点数比较的底层机制。首先介绍了IEEE 754双精度浮点数标准，包括64位存储结构（1位符号、11位指数、52位尾数）及其数值计算公式。重点剖析了0.1+0.2≠0.3的经典问题，指出这是由于十进制转二进制时产生的无限循环小数无法精确存储导致的舍入误差。此外还探讨了浮点数的特殊值（±0、±Infinity、NaN）处理方式及比较规则，并提供了BigInt等解决方案。文章通过数学原理和计算机存储结构的双重角度，揭示了JavaScript数值比较中常见陷阱的本质原因。

js中0.1+0.2 != 0.3

zhouyuzhu666的博客

10-18

491

console.log(0.1+0.2);//0.30000000000000004 在js中0.1+0.2的结果不等于0.3，这是由于精度缺失造成的，JS数字采用IEEE 754 双精度 64 位浮点数来存储,在js中数字只能保存小数点后52位，第53位为0省略，为1进1，0.1的二进制加0.2的二进制的和第53位是1，向前进1，后面的省略，所以转换成十进制不等于0.3 实际得到的0.2的二进制加0.3的二进制的结果为 0.0100110011001100110011001100110011001100

JS中0.1+0.2 !== 0.3的原因以及如何解决此问题

m0_52743009的博客

02-14

1631

JavaScript中0.1+0.2 !== 0.3的原因，以及如何解决0.1+0.2不等于0.3的问题

js中 0.1 + 0.2 != 0.3 为什么？

weixin_63811578的博客

10-19

542

js表达式 0.1 + 0.2 == 0.3 这个表达式看起来是没有问题的但是实事如此并非如此，这个属于js运算中精度缺失的问题所以这个表达式不成立 0.1 + 0.2!= 0.3因为计算机存储数据时，是以二进制（10101010）形式进行存储的。所以计算机计算0.1+0.2的时候，实际上是基计算的两个数的二进制的和这两个数的二进制都是无限循环的数。

JS中0.1+0.2！=0.3

shenzhou_yh的博客

05-23

1802

现象： console.log(0.1+0.2);//0.30000000000000004 原因 1、存储原理在计算机中数字无论是定点数还是浮点数都是以多位二进制的方式进行存储的。在JS中数字采用的IEEE 754的双精度标准进行存储(存储一个数值所使用的二进制位数比较多,精度更准确) 2、示例在定点数中，如果我们以8位二进制来存储数字。对于整数来说，十进制的35会被存储为： 001...

JS中0.1+0.2 !== 0.3 的原因及解决办法

Allen-Ye博客

08-11

7093

在JavaScript中，如果判断0.1 + 0.2 === 0.3，结果是false，就像这样： console.log(0.1 + 0.2 === 0.3); // false console.log(0.1 + 0.2); // 0.30000000000000004 这是怎么回事呢？0.1 + 0.2竟然不等于0.3？是程序出问题了吗？原来JavaScript采用的是IEEE754的64位双精度版本，由三部分组成： 1位数符：标记正负，0为正，1为负 11位阶码：数字的整数部分 52位尾数：数字

JS中0.1+0.2 != 0.3的原因及解决方法

afloatboat的博客

06-14

1261

JS中0.1+0.2 //0.1+0.2 console.log(0.1 + 0.2)//0.30000000000000004 console.log(0.1+0.2==0.3)//false //在它们相加的时候，两个近似值(50位)进行了计算，导致最后的结果出现 //0.30000000000000004，此时对于JS来说，其不够近似于0.3，所以出现了0.1+0.2 != 0.3 //解决方法： console.log(Number(0.1+0.

js中的0.1+0.2!==0.3

weixin_33907511的博客

04-01

394

本文主要是意识流写法，想到哪写到哪，估计有些废话，自行过滤（逃...）。前端开发应该都知道这是浮点数运算一个经典的问题了，网上关于这个问题的文章也一抓一大把，以前对这个问题也只是非常粗浅的知道这是浮点数的精度问题，具体原因并没有深究过，偶然又碰到一个与这个问题相关的问题，就再捋一下,深层次理解下。遇到的问题和不理解的地方 0.1+0.2 !=0.3 安全整数范围MDN上是（-（2^53 ...

js 0.1+0.2 !== 0.3 简单解决方案

宏斌的博客

12-28

543

export const round = number => { const getFloat = number.toString().split("."); if (getFloat.length === 1) { return number; } const floatLength = getFloat[1].length; if (floatLength > 6) { return Math.round(number.toFixed(2) * 100)

在javascript中0.1+0.2 !== 0.3 ，为什么？如何才能让其相等？

Sherry Tian的博客

08-12

589

在js中为何0.1+0.2 !== 0.3 ？如何才能让其相等？

js数据比较的特殊情况——0.1+0.2！=0.3 、NaN!=NaN

wangxiuyan0228的博客

04-27

628

1、null和undefinednull==undefined //truenull===undefined //false实际上，undefined值是派生自null的值，因此ECMA-262规定对他们的相等性测试都要返回true2、0.1+0.2！=0.3 0.1+0.2==0.3 //false0.05+0.25==0.3 //truejs的Number类型使用IEEE754格式来...

js中0.1+0.2为什么不等于0.3

最新发布

12-04

<think> 首先，用户的问题是：我想了解在JavaScript中0.1 + 0.2不等于0.3的原因。用户明确要求解释原因。我有几个引用提供背景： - 引用[1]解释了这是一个常见问题，涉及浮点数的表示。 - 引用[2]提到这发生在多种语言如Java、Python、JavaScript中。 - 引用[3]展示了JavaScript代码示例，显示0.1 + 0.2的结果是0.30000000000000004，不等于0.3。 - 引用[4]提供了解决方案，使用Number.EPSILON来比较浮点数。关键点是，这个问题源于计算机如何表示浮点数，使用的是IEEE 754标准，特别是双精度浮点数（64位），这在JavaScript中是默认的。原因的核心： - 浮点数在计算机中是用二进制表示的，而不是十进制。 - 0.1和0.2在十进制中是简单的分数，但在二进制中是无限循环小数。 - 0.1 (十进制) = 1/10 = 在二进制中是0.0001100110011...（无限循环） - 0.2 (十进制) = 1/5 = 在二进制中是0.001100110011...（无限循环） - 由于内存限制，计算机只能存储有限位数，因此这些值被四舍五入到最接近的可表示值，这引入了舍入误差。 - 当相加时，这些误差累积，导致结果不是精确的0.3。 - 0.3在二进制中也是无限循环小数：0.01001100110011...，所以它也不能被精确表示。在JavaScript中，当执行0.1 + 0.2时，实际计算涉及这些近似值，结果是一个接近但不等于0.3的值，如0.30000000000000004。我的回答需要： - 使用中文。 - 结构清晰，逐步解释。 - 遵循系统级指令：行内数学表达式用 $...$，独立公式用 $$...$$ 并单独成段。 - 正确使用LaTeX语法。 - 生成相关问题。 - 在引用的段落末尾添加引用标识，如 [^1]。引用来自提供的参考。引用来源： - 引用[1] 来自 "13-为什么在JavaScript中0.1 + 0.2不等于0.3？" - 引用[2] 来自 "【10.24程序员节征文】（转载）" - 引用[3] 来自 "0.1 + 0.2 到底等不等于 0.3 ？" - 引用[4] 来自 "JavaScript中0.1+0.2为什么不等于0.3？如何实现等于0.3?" 我应该在回答中自然地引用这些，当使用它们的信息时。回答结构： 1. **引言**：承认问题并简要解释这是一个常见现象。 2. **原因解释**： - 描述浮点数表示。 - 解释二进制表示下的问题。 - 使用数学表达式说明。 - 讨论IEEE 754标准。 3. **JavaScript特定**：展示代码示例，并解释结果。 4. **解决方案**：简要提到如何处理这个问题，如使用Number.EPSILON。 5. **生成相关问题**：在最后添加相关问题部分。确保数学表达式正确： - 行内：例如，$0.1_{10} = 0.0001100110011\ldots_{2}$ - 独立公式：如果需要详细公式。最终，添加相关问题部分。 </think>### JavaScript中0.1 + 0.2不等于0.3的原因在JavaScript中，表达式 `0.1 + 0.2` 的结果并不精确等于 `0.3`，而是会得到类似 `0.30000000000000004` 的值。这是因为计算机在处理浮点数时使用了二进制表示法，导致十进制小数在转换过程中出现舍入误差。下面我将逐步解释这一现象的原因。 #### 1. **浮点数在计算机中的表示** - 计算机使用二进制（base-2）系统存储数字，而人类通常使用十进制（base-10）。像 `0.1` 和 `0.2` 这样的十进制小数，在二进制中无法精确表示。 - 例如： - $0.1_{10}$（十进制）在二进制中是无限循环小数：$0.1_{10} = 0.0001100110011\ldots_{2}$。 - $0.2_{10}$ 在二进制中也是无限循环小数：$0.2_{10} = 0.001100110011\ldots_{2}$。 - 计算机使用 IEEE 754 标准（双精度浮点数）存储浮点数，该标准只有64位空间（1位符号位、11位指数位、52位尾数位）。因此，无限循环的二进制小数必须被截断和四舍五入，导致精度损失[^1][^2]。 #### 2. **舍入误差的累积** - 当 `0.1` 和 `0.2` 被转换为二进制浮点数时，它们会被近似存储： - $0.1 \approx 1.10011001100110011001101 \times 2^{-4}$（在 IEEE 754 中）。 - $0.2 \approx 1.10011001100110011001101 \times 2^{-3}$。 - 在加法操作中： $$ 0.1 + 0.2 \approx (1.10011001100110011001101 \times 2^{-4}) + (1.10011001100110011001101 \times 2^{-3}) $$ 由于指数不同，需要对齐后进行加法，这会放大舍入误差。最终结果近似为： $$ 0.3000000000000000444089209850062616169452667236328125 $$ 在JavaScript中，这个值被简化为 `0.30000000000000004`[^1][^3]。 - 相比之下，`0.3` 在二进制中也是无限循环小数：$0.3_{10} = 0.01001100110011\ldots_{2}$，因此它同样无法精确存储。计算机存储的 `0.3` 是一个近似值，但 `0.1 + 0.2` 的计算结果不等于这个近似值[^2]。 #### 3. **JavaScript中的验证** - 在JavaScript中运行以下代码，可以看到结果： ```javascript console.log(0.1 + 0.2); // 输出: 0.30000000000000004 console.log(0.1 + 0.2 === 0.3); // 输出: false ``` 这是因为 `0.1 + 0.2` 的实际结果略大于 `0.3`，而 JavaScript 使用严格的相等比较（`===`），因此返回 `false`[^3][^4]。 - 这不是JavaScript独有的问题，而是所有使用 IEEE 754 浮点数的语言（如Python、Java）中的常见现象[^2]。 #### 4. **如何避免或处理这个问题** - 在需要精确比较时，不要直接使用 `==` 或 `===` 比较浮点数。可以使用容差（tolerance）方法： ```javascript // 使用 Number.EPSILON（ES6引入，表示最小的浮点数误差） function isEqual(a, b) { return Math.abs(a - b) < Number.EPSILON; } console.log(isEqual(0.1 + 0.2, 0.3)); // 输出: true ``` `Number.EPSILON` 的值约为 $2^{-52} \approx 2.220446049250313 \times 10^{-16}$，它定义了可接受的误差范围[^4]。 - 或者，将浮点数转换为整数进行计算（例如，以分为单位处理金额）。总之，`0.1 + 0.2 !== 0.3` 的原因在于二进制浮点数表示的局限性，导致舍入误差在算术运算中累积。这不是bug，而是计算机科学中的基本限制[^1][^3]。