力扣刷题-11盛最多水的容器

问题：

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1：

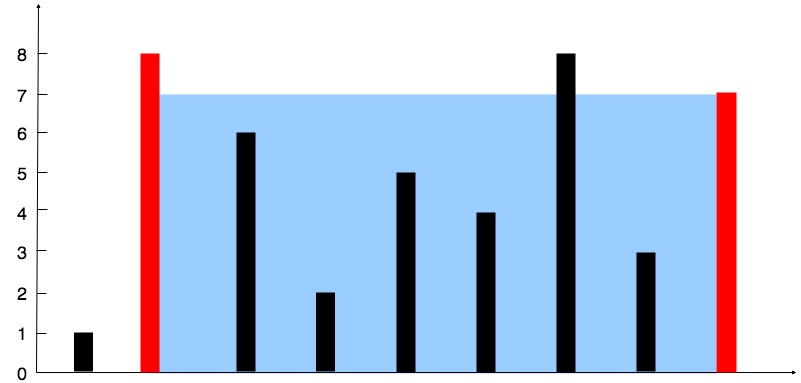
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

要求：

• n == height.length
• 2 <= n <= 10^5
• 0 <= height[i] <= 10^4

错误原因：

这道题最开始一直错在时间超时，最开始超时，由于时间复杂度为O（n^2），但实际上只需要O（n），最开始的思路是设置两个指针，一个指针不动，另外一个指针从它的下一个位置遍历到后面所有的位置，然后不动的指针向后挪一个位置，继续循环执行一样的操作，选择一个临时变量，记录最大的值。

解题思路：

由于题目要求是求得最大的盛水，所以我们建立两个指针，这两个指针分别指向数组为0，和数组的最末尾的长度。我们设置分别为left和right

现在先给max_height=（right-left）*min(height[right],height[left]);

我们根据height[right],height[left]的大小比较，进行挪动

这里我们假设right的小于left

所以此时体积为

此时我们分两种情况

①移动left指针

则此时我们的right-left变小,此时我们将移动后的left记为left'

此时有两种可能，第一种是height[right]>height[left']

所以此时体积变小。此时体积为

第二种是height[right]<height[left']

此时体积为

②移动right指针

由①可知，移动left指针只会让体积变小，而移动右指针，一旦height[right]>height[left]，则存在体积变大的可能

综上，可以得出解题思路。

代码实现

class Solution {
    public int maxArea(int[] height) {
        if(height.length==0||height.length==1){
            return 0;
        }
        int temp=0;
        int left = 0,right = height.length-1;
        int max_height = 0;
        while(left<right){
             max_height=(max_height>(right-left)*min(height[left],height[right]) )? max_height:(right-left)*min(height[left],height[right]);
            if(height[left]>height[right]){
                right--;
            }
            else{
                left++;
            }
        }
        return max_height;
    }
    public int min(int a1,int a2){
        if(a1<a2){
            return a1;
        }
        return a2;
    }
}