计算机图形学入门16：曲线

1.曲线

        曲线（Curves）在图形学中应用非常广泛，比如：相机的拍摄路径、物体的移动路径、动画曲线、矢量字体等。如下图所示，是使用曲线到矢量字体的应用，通过移动一些控制点来改变字体。

2.贝塞尔曲线

2.1 贝塞尔曲线定义

        从上图中，如果无限的放大曲线的某一块区域，任何地方都是光滑的。这就是贝塞尔曲线(Bezier Curves)。

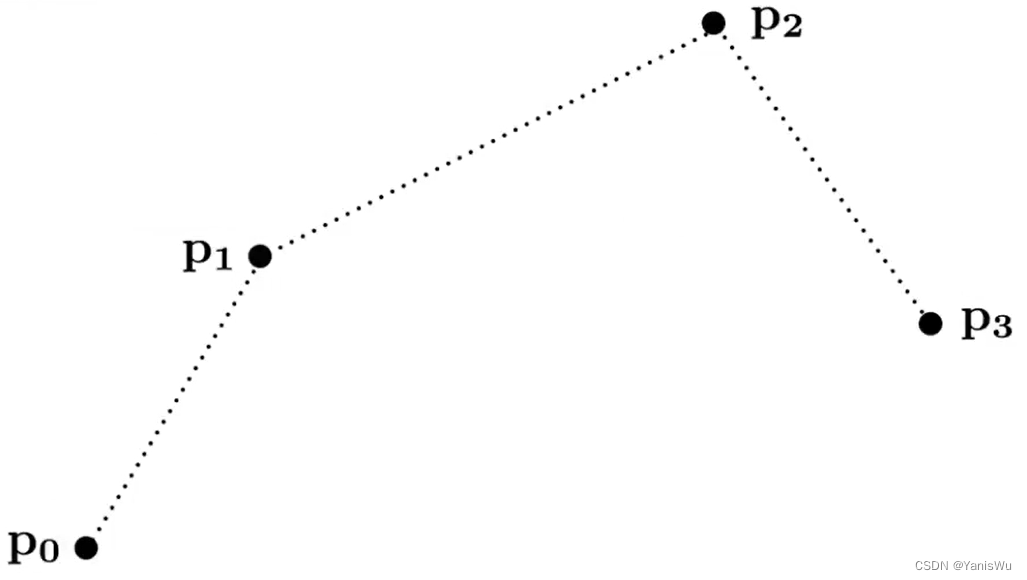
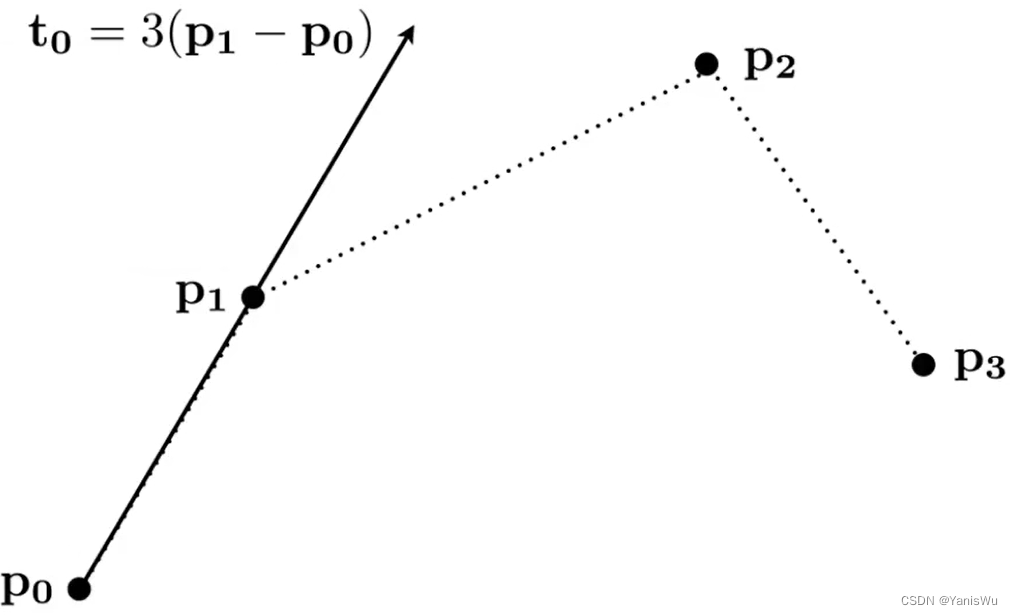
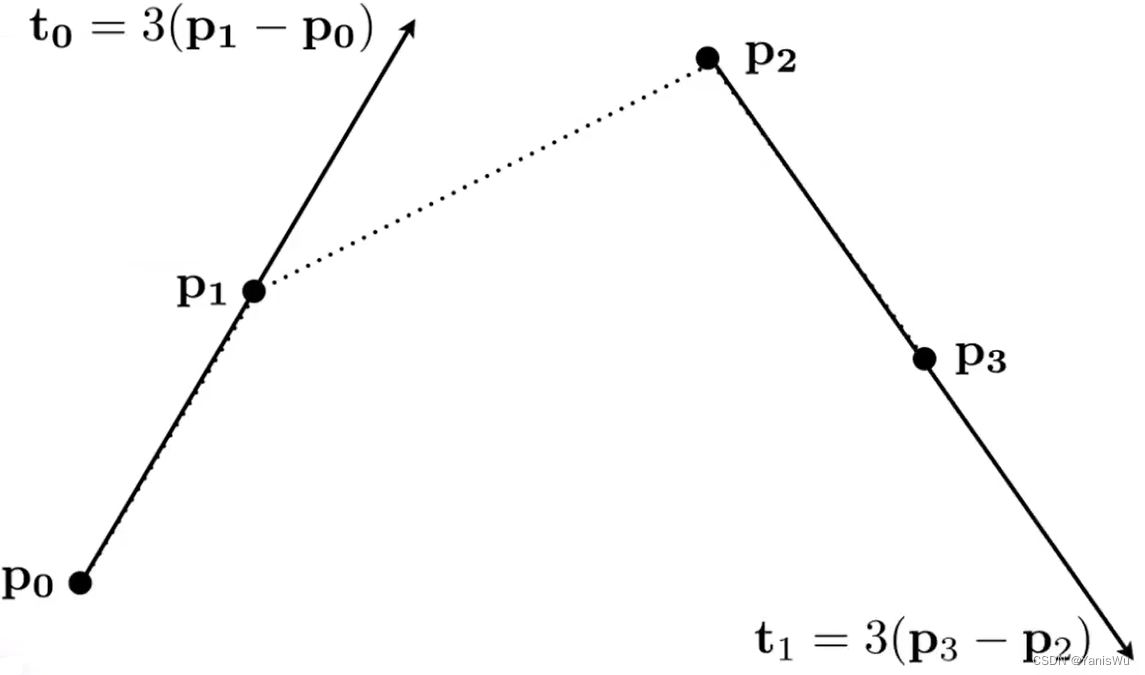
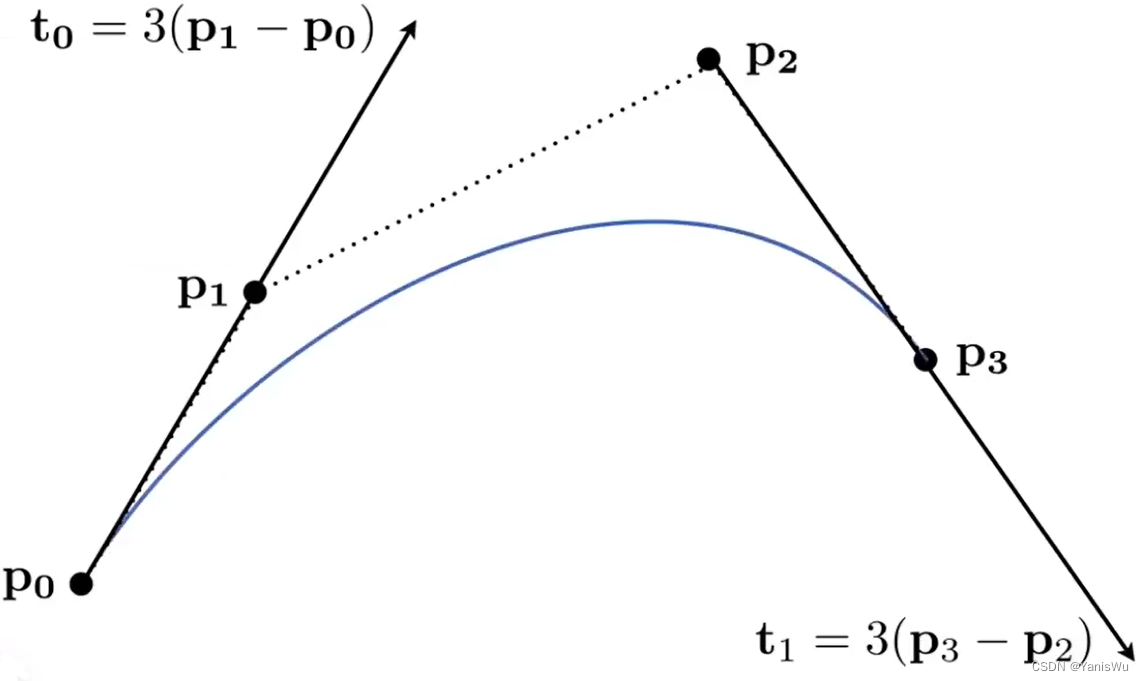
        贝塞尔曲线是通过一系列控制点进行定义的曲线。而这些控制点满足一些性质，比如要满足从P0点开始，并且沿着P0P1方向，结束沿着P2P3方向，到P3点结束。曲线不必经过所有控制点，但必须经过起始点和结束点。这样就定义了一条贝塞尔曲线，如下图所示。

2.2 绘制贝塞尔曲线

        那么，如何使用任意点绘制贝塞尔曲线呢？

        贝塞尔曲线的绘制算法是 De Casteljau's Algorithm，算法的基本思想是利用线性插值的原理，将高阶贝塞尔曲线转化为一阶贝塞尔曲线的组合。

        下面，我们以 3 个控制点绘制贝塞尔曲线的例子来进行介绍。

        N 个控制点绘制的贝塞尔曲线，称为 N-1 阶贝塞尔曲线。如下图所示，我们定义了 3 个控制点，由此绘制的贝塞尔曲线称之为 二阶贝塞尔曲线（Quadratic Bezier）。对于这 3 个控制点，我们首先对相邻控制点进行连线。

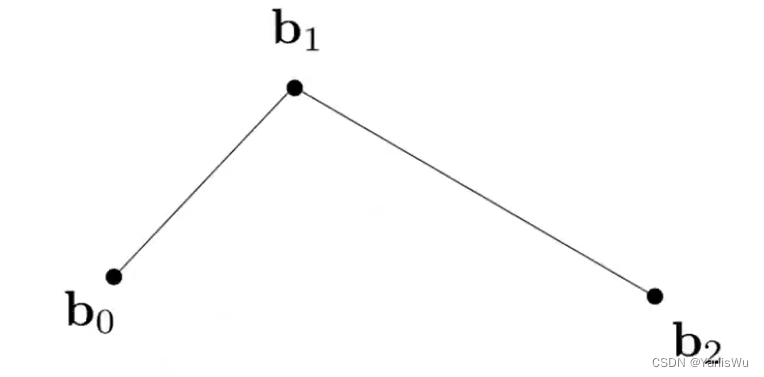
        定义一个变量 t，其值的范围为 [0, 1]，作为算法的输入值。当 t = 0