《机器学习》周志华习题1.2的解答

最新推荐文章于 2025-01-14 17:39:16 发布

原创最新推荐文章于 2025-01-14 17:39:16 发布

· 2.2k 阅读

7 ·

版权

文章标签：

#机器学习 #python

python 同时被 2 个专栏收录

5 篇文章

订阅专栏

机器学习

3 篇文章

订阅专栏

本题解答参考：

1.优快云博主「是你的小鱼」：

https://blog.youkuaiyun.com/yuzeyuan12/article/details/83113461

2.优快云博主「四去六进」：

https://blog.youkuaiyun.com/yuzeyuan12/article/details/83113461

题目理解：

题目：

与使用单个合取式来进行假设表示相比，使用“析合范式”将使得假设空间具有更强的表示能力。若使用最多包含k个合取式的析合范式来表达1.1的西瓜分类问题的假设空间，试估算有多少种可能的假设。

在刚看到此题时，首先我想到的是，利用与解1.1类似的方法，将各个假设进行编码，并定义各编码之间的合取与析取运算，如将色泽属性分别编码：青绿：01 乌黑：10 （通配）*：11。如此，则假设：（色泽=青绿）∧(根蒂=稍蜷)∧(敲声=沉闷) $（色泽=青绿）∧(根蒂=稍蜷)∧(敲声=沉闷)$ 编码为：01010100。

基于此，定义假设之间的析取运算即是将析取的两个编码按位相与，便可得结果。

但此种做法存在极大不便，首先，析取的结果所形成的集合无法与假设空间形成满射，例如假设色泽=青绿∧(根蒂=稍蜷)∧(敲声=沉闷)与假设色泽=青绿∧(根蒂=硬挺)∧(敲声=浊响) 相析取，即01010100与01100001按位相或，所得结果为01110101，该结果编码没有对应的键值，导致最终计算的失败。其次，该编码方式不具备良好的处理亢余的能力，因此不可行。

之后我阅读博主[四去六进][2]关于本题的解答，同样对用栈的方式遍历组合的方法表示深刻的怀疑，原因博主[是你的小鱼][1]在其文章中解释的十分清楚，在此我作一些简单的解读。

题目要求从48种假设里面取k个假设进行析取，然后列出所有可能的组合用来表示假设空间，如果不考虑亢余情况，此题很简单，假设空间的大小即是C48k

但问题在于，由于48种假设中存在通配的情况，故而不可避免的要出现亢余，这样的话，我们就需要将这些亢余从假设空间剔除出去。

剔除的方法便在于理解亢余的本质，48中假设中，只有18种假设不包含通配情况，它们之间的析取不会产生亢余，我们将其称为叶子假设。需要注意的是，任何一种包含通配的假设，都可以表示为叶子假设的析取。

故而我们可以按位将18种叶子假设进行编码，当前位为1意味着对应的叶子假设被包含，如（青绿，蜷缩，浊响）编码为100000000000000000，同时由于通配表示叶子假设的析取，即包含通配的假设中有多位为1，例如(*,*,清脆)编码为000111000000111000

进一步地，我们给出假设空间并消除亢余的步骤，如下：

取48种假设中的k元组合。
对此k个假设进行析取运算，即按位相或。
将所得的结果存入一个集合A，若集合A为空集，则直接添加进去，若A非空，则后续的结果需先与集合A中所有的元进行比较，若有相同的，则舍去该结果，这一步便实现了亢余的剔除。
遍历C48k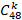的所有组合，得最终的假设空间A，A中元素的数目变为假设空间的大小。

图示：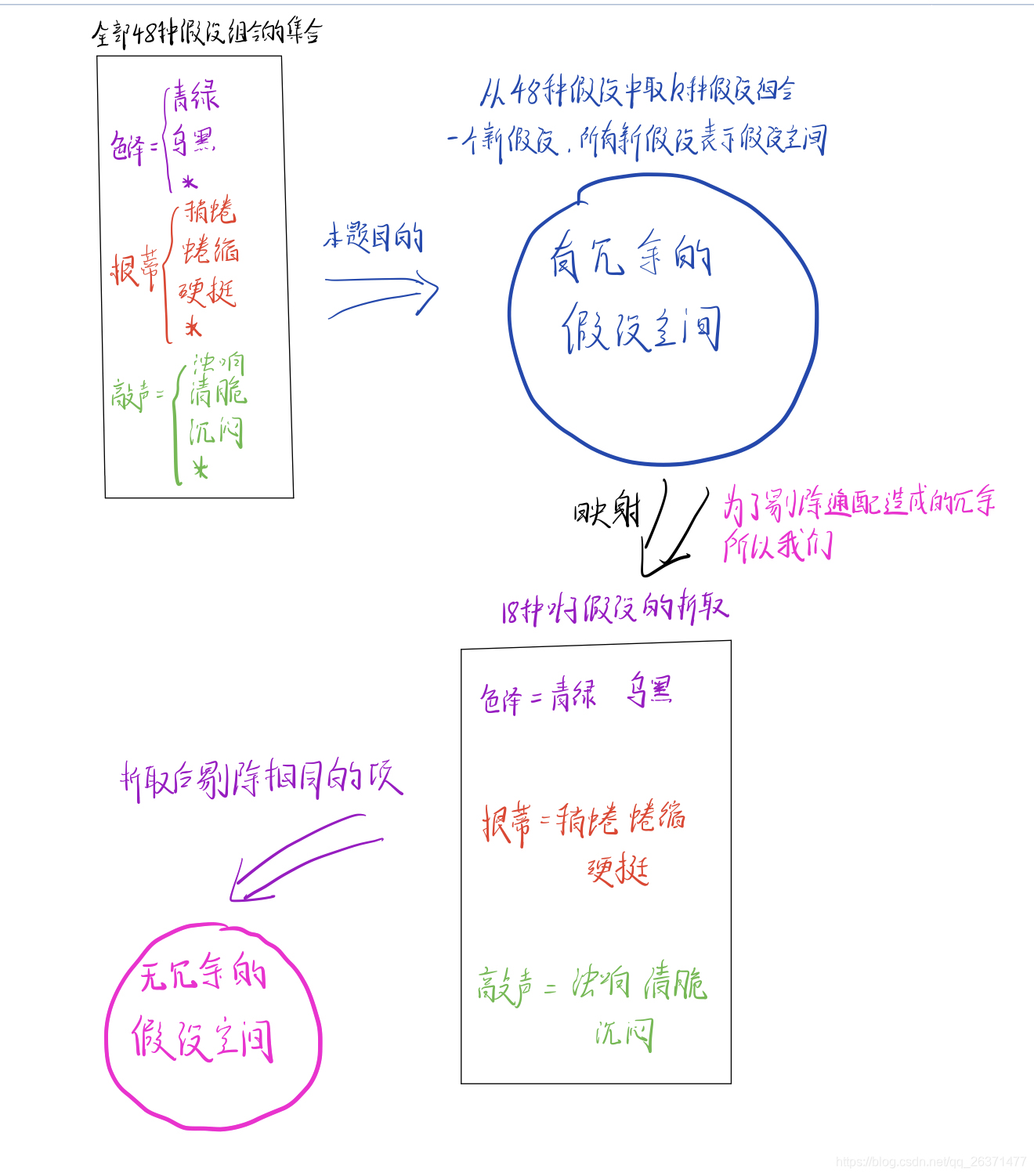

代码实现：

博主「是你的小鱼」提供了它的代码，根据网友反馈跑不起来，故在这里我给出我的代码。

代码采用python3.7实现，加载itertools进行迭代运算用于组合数的处理，中间运用了运算符重载，将假设的析取用类的“+”运算表示。

# -*- coding: utf-8 -*-
"""
Created on Sat Sep 21 14:36:27 2019

@author: Administrator
"""
import itertools 
import time


#将数存储为数组
def method(value):
    #divmod()是内置函数，返回整商和余数组成的元组
    result = []
    for i in range(len(value)):
        result.append(eval(value[i]))
    return result

#用类表示编码，并定义重载的运算符 + 为析取
class WMcode:
    val  = ''
    len  = 0
    def __init__(self, strv):
        self.val = method(strv)
    def __add__(self,other):             #析取运算
        strv = [] 
        for i in range(len(self.val)):
            addr = self.val[i]+other.val[i]
            if addr >= 2:
                addr = 1
            strv.append(str(addr))
        return WMcode(strv)
    def __or__(self,other):              #合取运算，本题未用到
        strv = [] 
        for i in range(len(self.val)):
            addr = self.val[i]*other.val[i]
            strv.append(str(addr))
        return WMcode(strv)
    
#对48中假设进行编码
nodes = [WMcode('100000000000000000'),WMcode('010000000000000000'),WMcode('001000000000000000'),
         WMcode('000100000000000000'),WMcode('000010000000000000'),WMcode('000001000000000000'),
         WMcode('000000100000000000'),WMcode('000000010000000000'),WMcode('000000001000000000'),
         WMcode('000000000100000000'),WMcode('000000000010000000'),WMcode('000000000001000000'),
         WMcode('000000000000100000'),WMcode('000000000000010000'),WMcode('000000000000001000'),
         WMcode('000000000000000100'),WMcode('000000000000000010'),WMcode('000000000000000001'),
         WMcode('100000000100000000'),WMcode('010000000010000000'),WMcode('001000000001000000'),
         WMcode('000100000000100000'),WMcode('000010000000010000'),WMcode('000001000000001000'),
         WMcode('000000100000000100'),WMcode('000000010000000010'),WMcode('000000001000000001'),
         WMcode('111000000000000000'),WMcode('000111000000000000'),WMcode('000000111000000000'),
         WMcode('000000000111000000'),WMcode('000000000000111000'),WMcode('000000000000000111'),
         WMcode('100100100000000000'),WMcode('010010010000000000'),WMcode('001001001000000000'),
         WMcode('000000000100100100'),WMcode('000000000010010010'),WMcode('000000000001001001'),
         WMcode('111000000111000000'),WMcode('000111000000111000'),WMcode('000000111000000111'),
         WMcode('100100100100100100'),WMcode('010010010010010010'),WMcode('001001001001001001'),
         WMcode('111111111000000000'),WMcode('000000000111111111'),WMcode('111111111111111111')]
#           （青绿，蜷缩，浊响） （青绿，稍蜷，浊响） （青绿，硬挺，浊响）
#           （青绿，蜷缩，清脆） （青绿，稍蜷，清脆） （青绿，硬挺，清脆）
#           （青绿，蜷缩，沉闷） （青绿，稍蜷，沉闷） （青绿，硬挺，沉闷）
#           （乌黑，蜷缩，浊响） （乌黑，稍蜷，浊响） （乌黑，硬挺，浊响）
#           （乌黑，蜷缩，清脆） （乌黑，稍蜷，清脆） （乌黑，硬挺，清脆）
#           （乌黑，蜷缩，沉闷） （乌黑，稍蜷，沉闷） （乌黑，硬挺，沉闷）
#           （*，蜷缩，浊响） （*，稍蜷，浊响） （*，硬挺，浊响）
#           （*，蜷缩，清脆） （*，稍蜷，清脆） （*，硬挺，清脆）
#           （*，蜷缩，沉闷） （*，稍蜷，沉闷） （*，硬挺，沉闷）
#           (青绿，*，浊响) （青绿，*，清脆） （青绿，*，沉闷）
#           (乌黑，*，浊响) （乌黑，*，清脆） （乌黑，*，沉闷）
#           (青绿，蜷缩，*) （青绿，稍蜷，*） （青绿，硬挺，*）
#           (乌黑，蜷缩，*) （乌黑，稍蜷，*） （乌黑，硬挺，*）
#           (*,*,浊响) (*,*,清脆) (*,*,沉闷)
#           (*,蜷缩，*) (*,稍蜷,*) (*,硬挺,*)
#           (青绿，*，*) （乌黑，*，*） （*，*，*）

#存储最终结果的集合A
A = []
#合取式数量k,在此进行改动即可
k = 3
#是否舍去当前假设标签abandon
abandon = 0
time_start=time.time()               #开始计时
comb = list(itertools.combinations(nodes,k))
for i in range(len(comb)):
    WMadd = WMcode('000000000000000000')
    for j in range(k):
        WMadd = WMadd + comb[i][j]
    for allval in A:                       #若A中已经存在当前假设，则舍去，因为这是亢余
        if WMadd.val == allval.val:
            print("symposis abandoned")
            abandon = 1
            break
    if abandon == 1:
        abandon = 0
        continue
    else:
        A.append(WMadd)
        print(WMadd.val, "is added")
    print("Present combination calculated")
time_end=time.time()                 #结束计时
print("Work is done")
print(len(A))
print('totally cost',time_end-time_start)