AES加密算法逆向分析

最新推荐文章于 2025-03-20 21:39:07 发布

原创最新推荐文章于 2025-03-20 21:39:07 发布 · 3.2k 阅读

11 ·

CC 4.0 BY-SA版权

文章标签：

#安全 #算法

AESEnc逆向分析

1. 观察程序执行流程

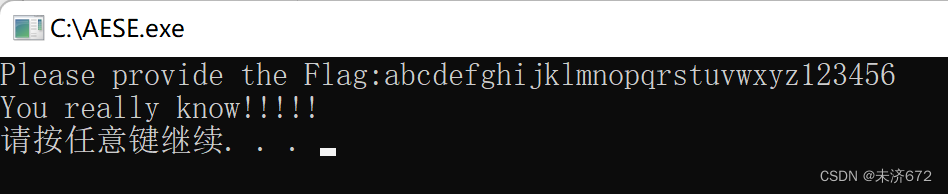
请添加图片描述
打开程序提示输入Flag，随意键入1个值之后程序输出“You really don’t know!!!”，即Flag错误。已知该程序是AES加密程序，由此猜测程序接受输入Flag之后经过AES加密的密文与某个给定字符串比较，若1致则输出成功，若不1致则输出失败。

2. 程序静态调试

2.1 main函数分析

如下图所示是main函数的数据准备阶段，在栈中初始化了1些1些变量备用，判断可能是密钥、指定字符串等。
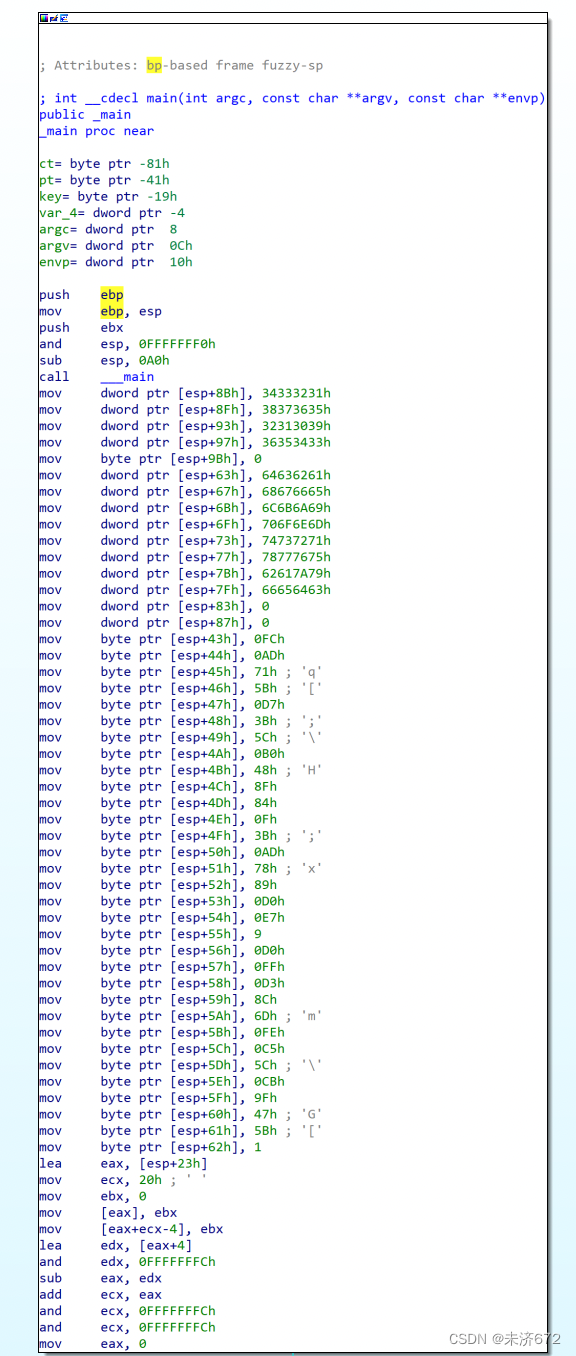
请添加图片描述
如下图所示是main函数的其余部分，程序使用printf函数输出“Please provide the flag:”，然后使用scanf函数读入字符串到esp+63h处，该处原为“abcd…wxyzabcdef”，判断此处输入为32个字节的字符串，且在输入之前被初始化为“abcd…wxyzabcdef”。

随后在栈中压入5个参数，第1个参数是20h即十进制32，接着压入esp+0A4h+ct即esp+23h位置的数据，同理压入在esp+63h位置的数据，压入10h即十进制16，压入在esp+8bh位置的数据。

通过观察第5个参数地址处的数据是字符串“1234567890123456”共计16个字节，暗合第4个参数10h，判断第4个参数是第5个参数的长度。

观察第3个参数地址处的数据发现是字符串“abcd…wxyzabcdef”共计32个字节，暗合第1个参数20h，判断第1个参数是第3个参数的长度。

第2个参数地址处为32个（初始化时ecx为20h、ebx为0、eax是esp+23h）字节的0，可能用于存储加密的结果，由之后的汇编代码可以验证。

总结该函数的调用：func(“1234567890123456”,v1的长度,输入的字符串,加密的结果,v3的长度)

随后可见1个循环，并依次见正确输出和错误输出，可以判断应为循环比较esp+23h处和esp+43h处的值是否相等，其循环变量为esp+9ch，初始化为0，条件是小于等于1fh即31d，还原其源代码应为for(int i=0;i<=32,i++)，只要有1个字节不同都会导致输出错误，循环完成后再次判断循环变量为32，输出成功并结束程序。

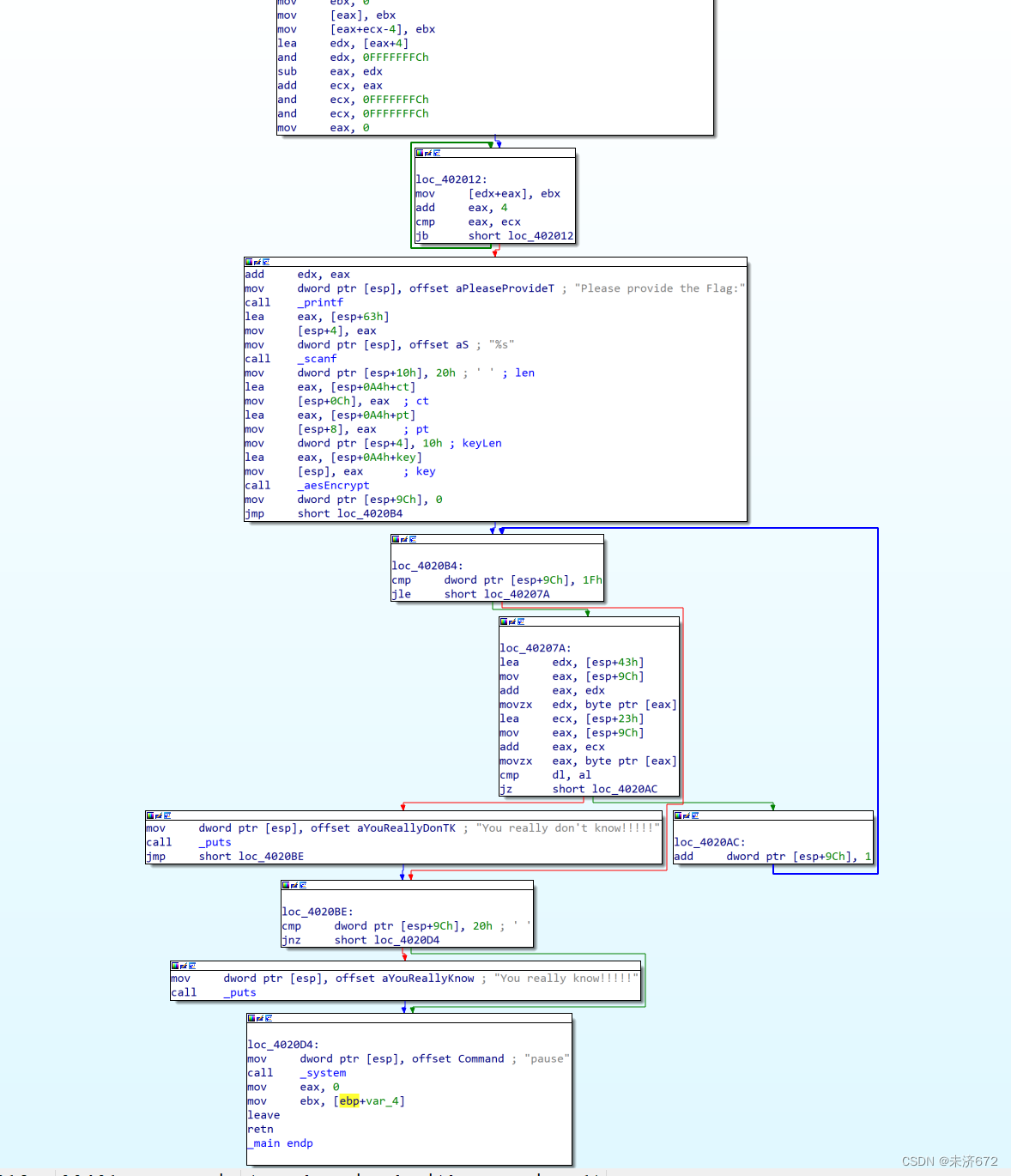
请添加图片描述
综上所述，已可由密钥和密文恢复明文：abcdefghijklmnopqrstuvwxyz123456。

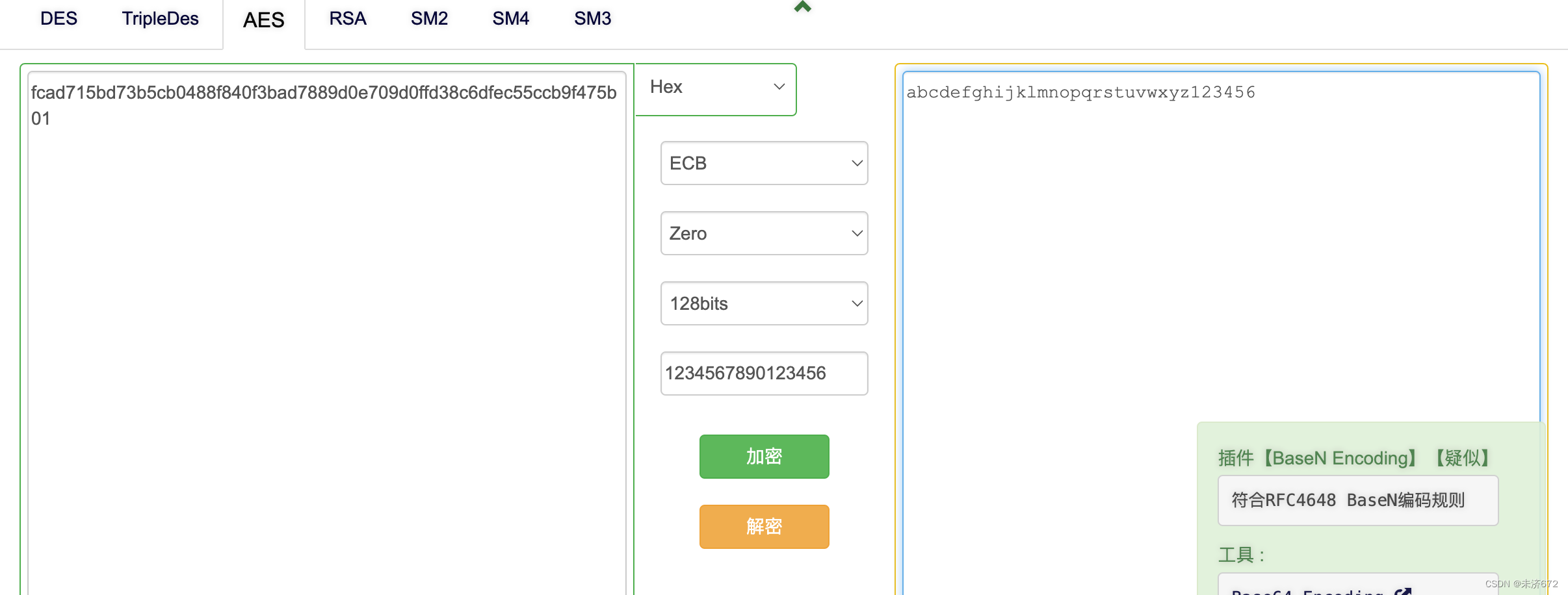
以此键入程序中，得到正确输出“You really know!!!”。

2.2 加密函数（aesEncrypt）分析

为在未知加密算法时进1步确认加密算法，需对加密函数进行分析。

由该函数调用：func(“1234567890123456”,v1的长度,输入的字符串,加密的结果,v3的长度)得知字符串“1234567890123456”很可能是密钥。

该函数的准备阶段不做赘述。

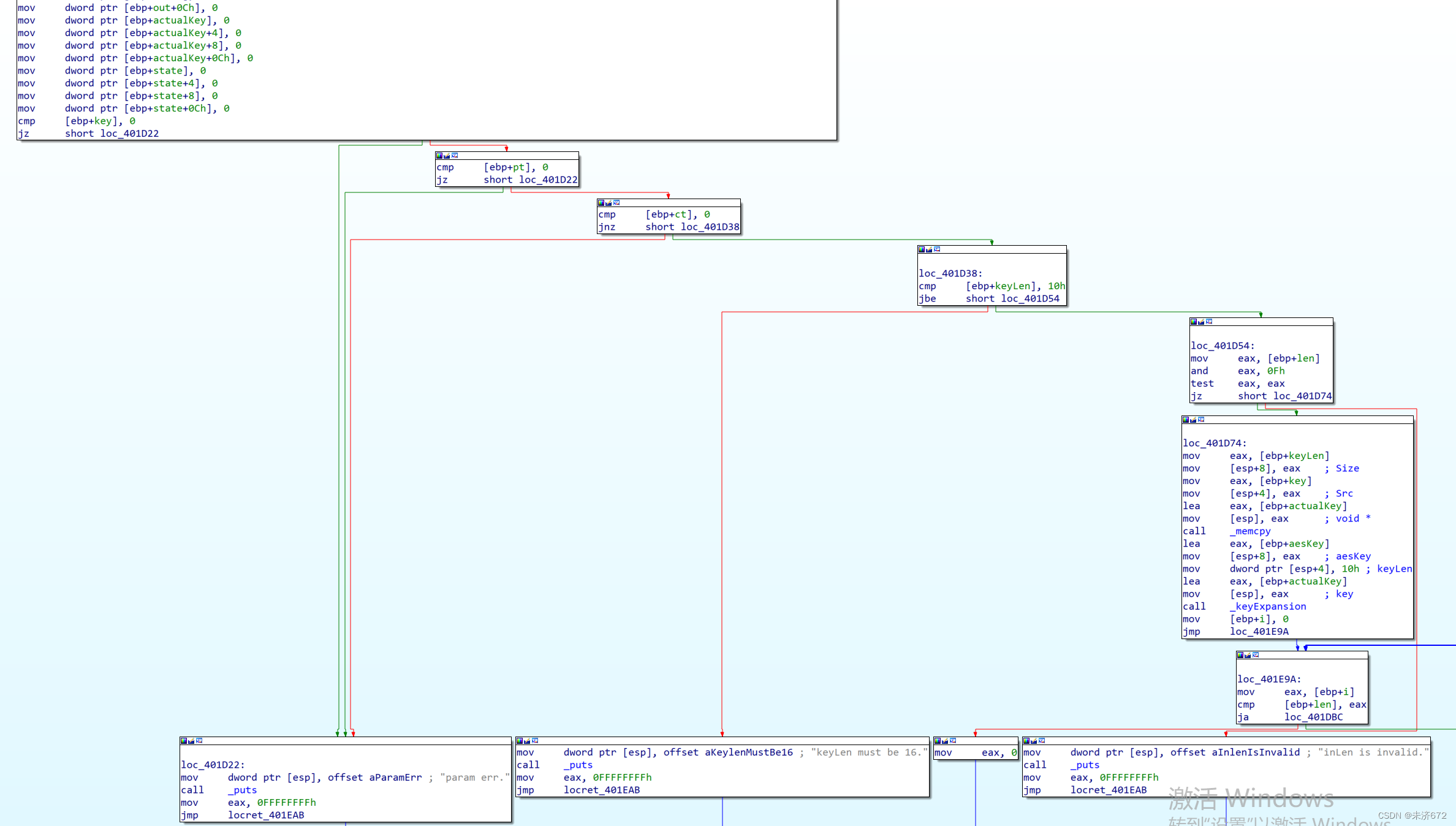
检查参数阶段：首先判断第1个参数是否为空，若空则报参数错误，再判断输入为空则报参数错误，接着判断结果存储位置不为空则报参数错误，继续判断v1即密钥的长度>16则报密钥长必为16，最后判断输入长度为16的倍数，如不是则报长度错误，以上任意1种错误都会导致程序异常退出。
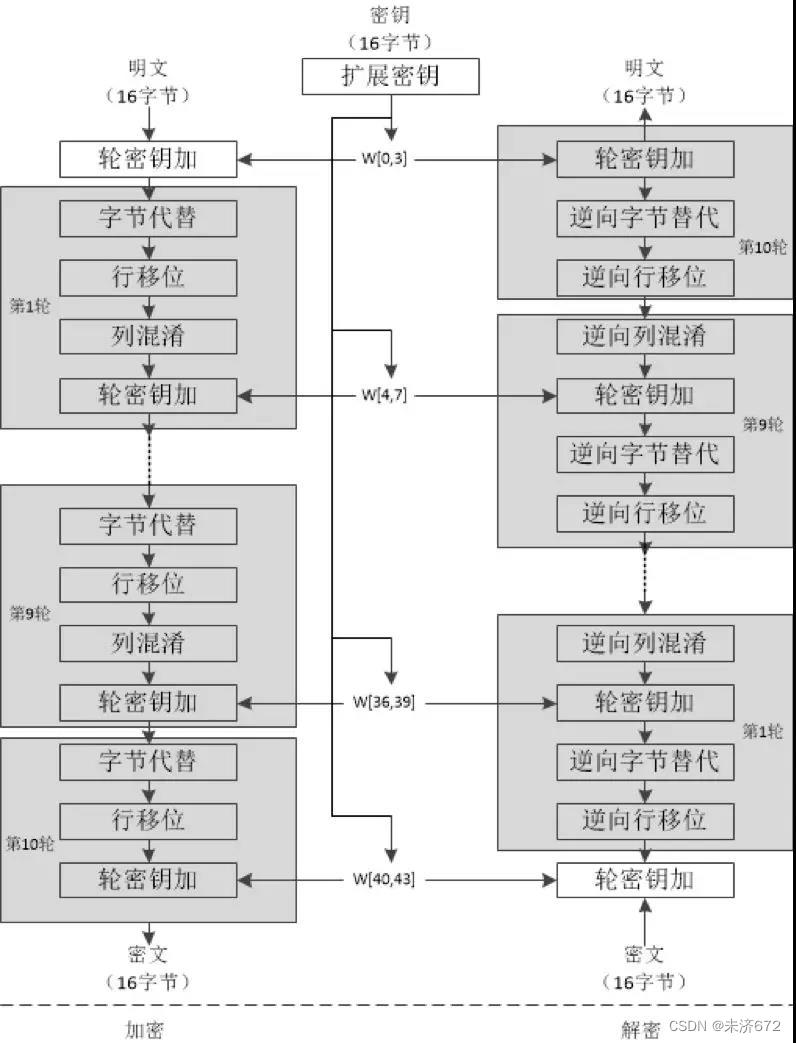
请添加图片描述
如下图所示为AES加解密算法流程图。

首先进行密钥扩展，如下图所示，将密钥长度，密钥和另1变量传入memcpy函数，把密钥拷贝到另1空间内以便稍后进行密钥扩展。随后向下1函数（密钥扩展）函数中传递密钥、密钥长、和某1结构体变量（应为扩展后的密钥）。
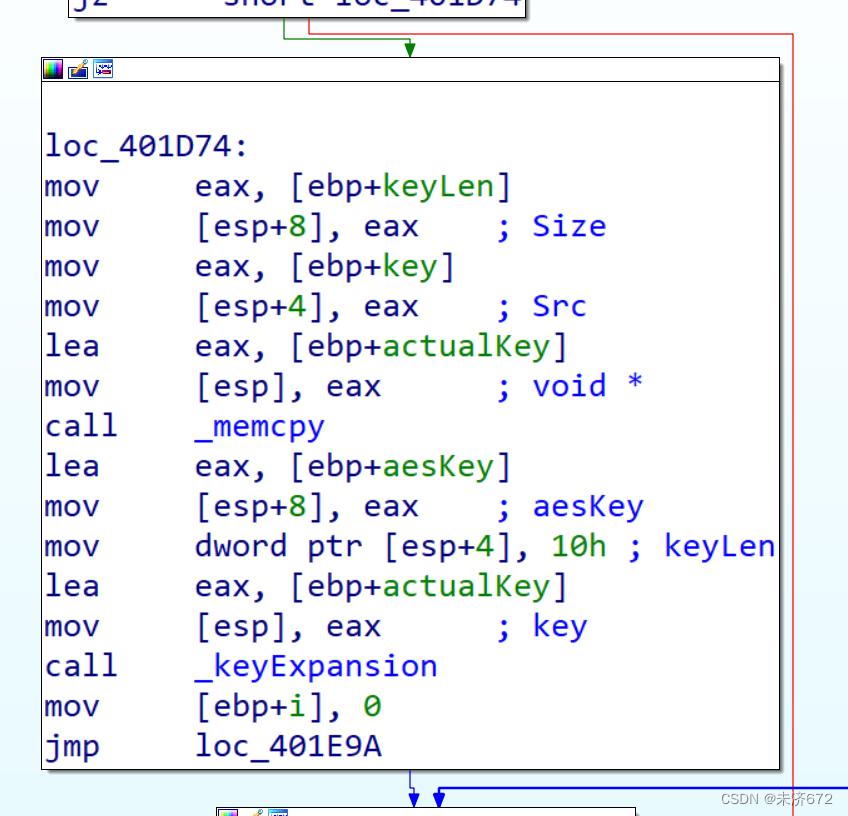
请添加图片描述
进入密钥扩展函数。

2.2.1 密钥扩展函数分析

参数检查阶段：若密钥空或扩展密钥非空则报参数错误，若密钥长不为16，报密钥长不受支持，并结束函数。
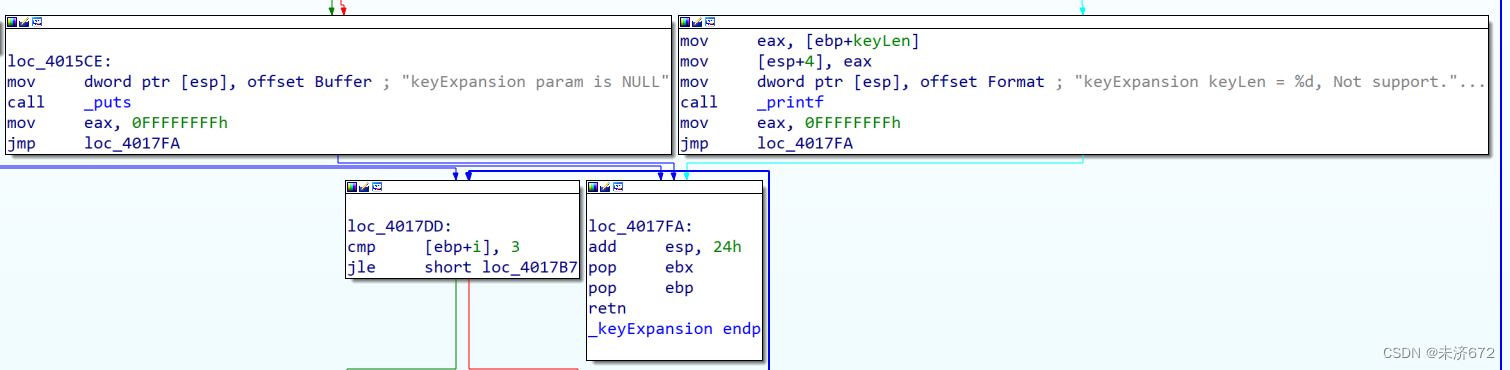
请添加图片描述
先将两个变量（此处参照源代码中定义）w、v赋值为aesKey结构体中的两个变量地址，再根据观察判断下1个变量为循环变量，命名为i，初始化为0，循环条件为小于等于3，因此该循环为4次，即for(int i=0;i<=3;i++)。
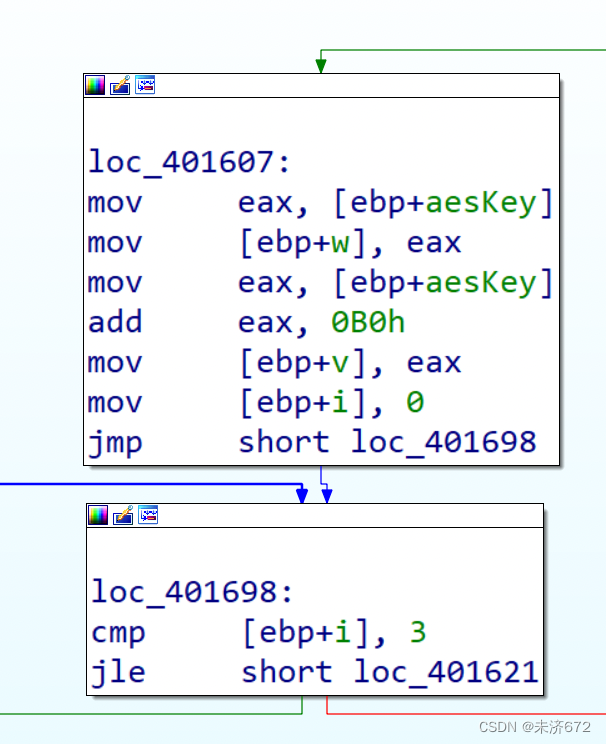
请添加图片描述
首先将初始密钥载入，如下图载入过程，以4字节为单位将密钥装入w[0]-w[3]中。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-024FZbdJ-1651719006092)(/Users/hurricane672/Desktop/AESEnc逆向分析.assets/image-20220504200051143.png)]
下图中的汇编代码先将key的第1字节取出，左移18h即24d位并装入edx的高8位，以此类推直到把edx的32d位都装满为止。把edx放置在w的相应位置上，循环变量加1，如此4轮将初试密钥全部载入。
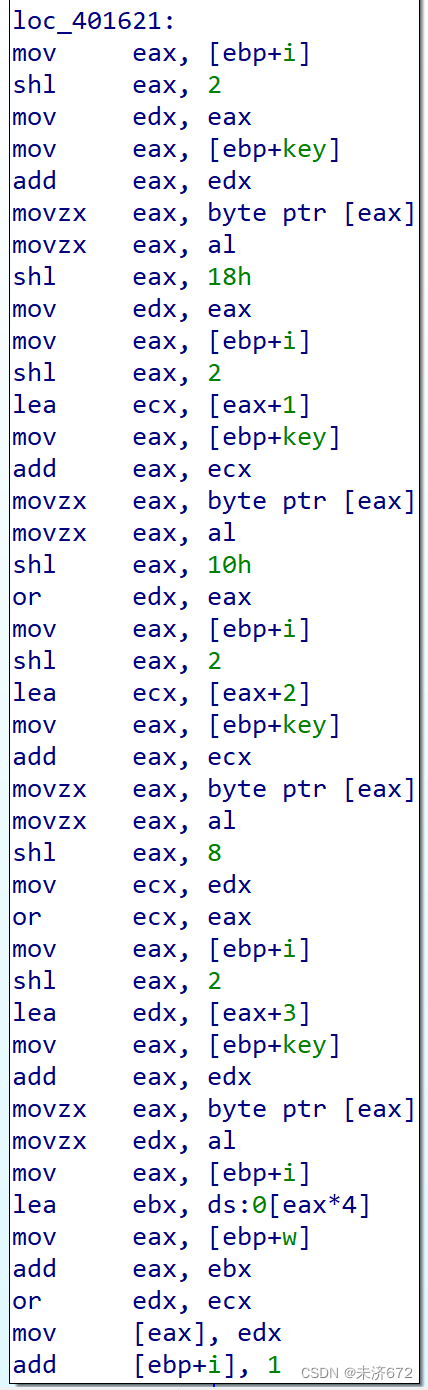
请添加图片描述
随后循环变量归零，开始10轮的密钥扩展循环。若非4的倍数则密钥以公式： $W [i] = W [i - 4] ⨁ W [i - 1]$ 确定；若为4的倍数则以公式： $W [i] = W [i - 4] ⨁ T (W [i - 1])$ 确定。

先看该部分的后半段。先取esp+w的地址（w变量的地址）+4获得w[1]的地址，取值存入ecx；再取w的地址+10h获得w[4]的地址，取值存入edx；最后取w的地址+14获得w[5]的地址，在该处存入edx和ecx相异或的值。如此依次做3次则得到了新1组密钥后3列的值，使w的地址整体+10h再反复9轮即可得到完整的扩展密钥。
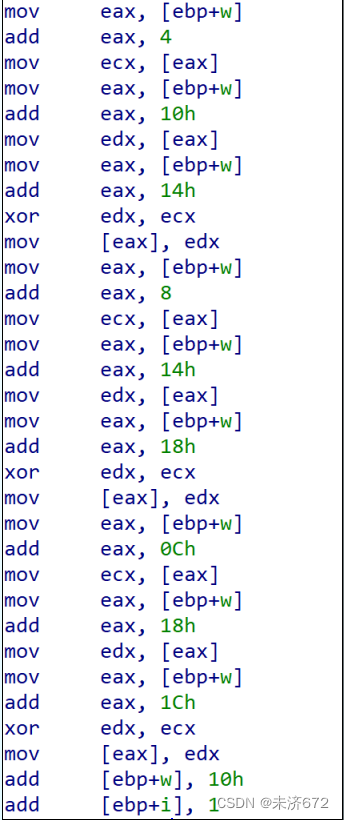
请添加图片描述
前半段较为复杂，T函数由3部分组成：

字循环:将1个字中的4个字节循环左移1个字节。即将输入字[b0, b1, b2, b3]变换成 [b1,b2,b3,b0]。
字节代换:对字循环的结果使用S盒进行字节代换。
轮常量异或:将前两步的结果同轮常量Rcon[j]进行异或，其中j表示轮数。轮常量Rcon[j]是1个字，其值见下表。

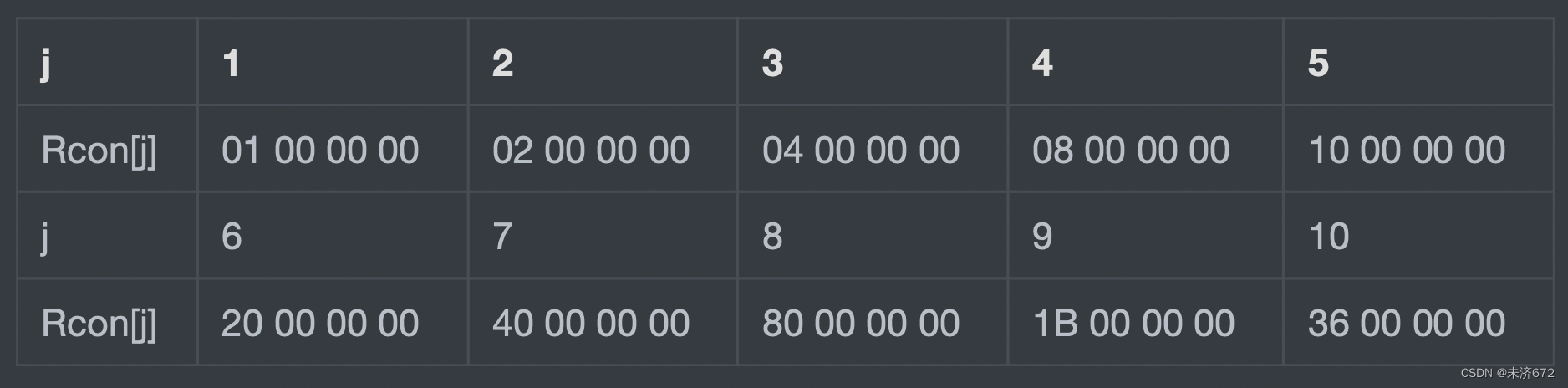
先取对应的值右移8的倍数位得到单个字节，用s盒替换，左移到对应的位置上，最后保存到ecx中，和edx中取出的轮常量异或存入对应位置。

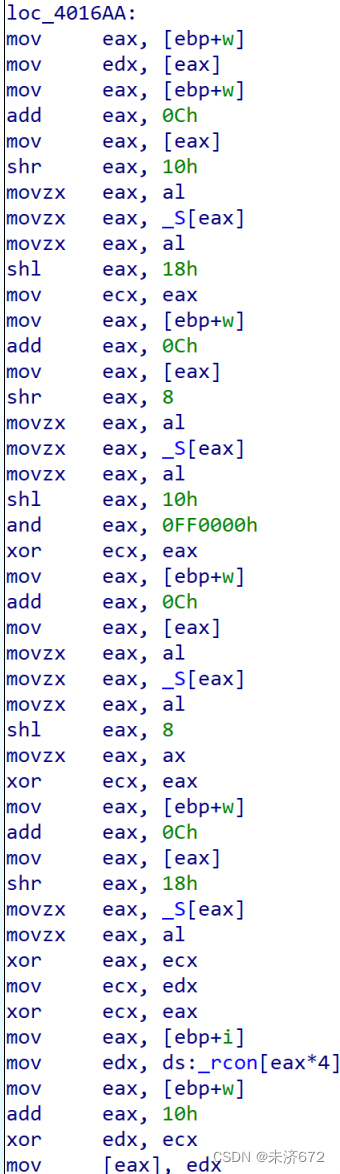
结束密钥扩展之后，w的指针指向数组的尾部，w逆向、v正向依次两层循环赋值得到整个解密密钥矩阵。

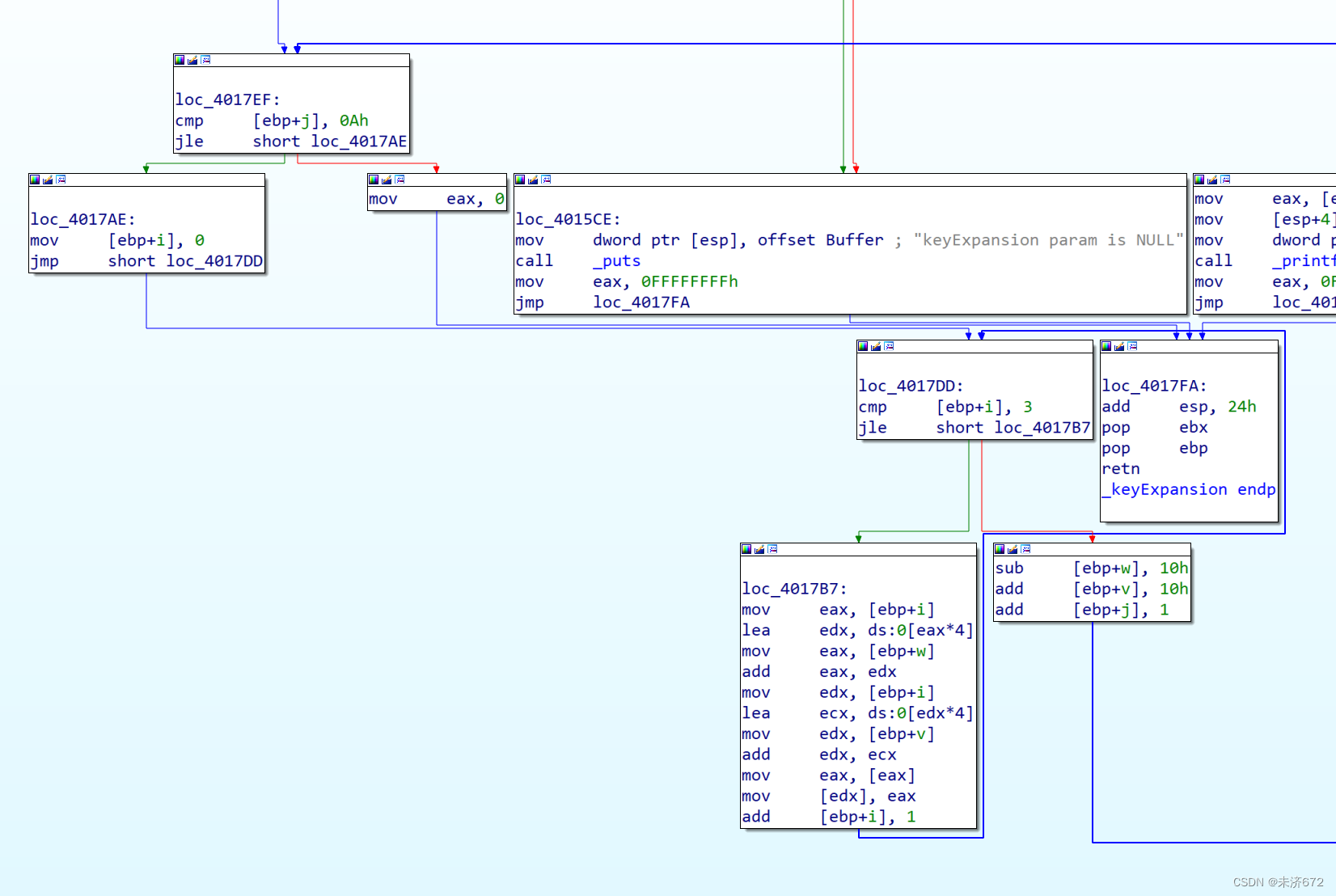
至此密钥扩展完成，返回上级函数。

循环变量i归零，开始对明文进行加密，循环次数为分组数对于输入“abcdefghijklmnopqrstuvwxyz123456”（32字节）分组数为2。

首先压入输入字符串地址和待处理矩阵（由数据初始化处可知为4*4的矩阵且初始化为0）作为参数，载入分组数据。
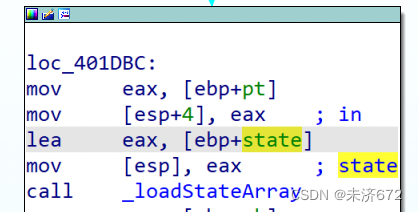
请添加图片描述

2.2.2 载入状态矩阵函数分析

进入该函数，如下图所示，是简单的双层循环，i、j分别对应矩阵的列和行，在in中去1字节放入eax中，eax中的值再放入state+j*4+i的位置上，由此推断源代码应为state[j][i]=*in，随后指针自增**（虽然此处指针先自增，但初值已经保存到eax，因此不影响）**、循环变量j自增。如此重复直到状态矩阵载入完毕。
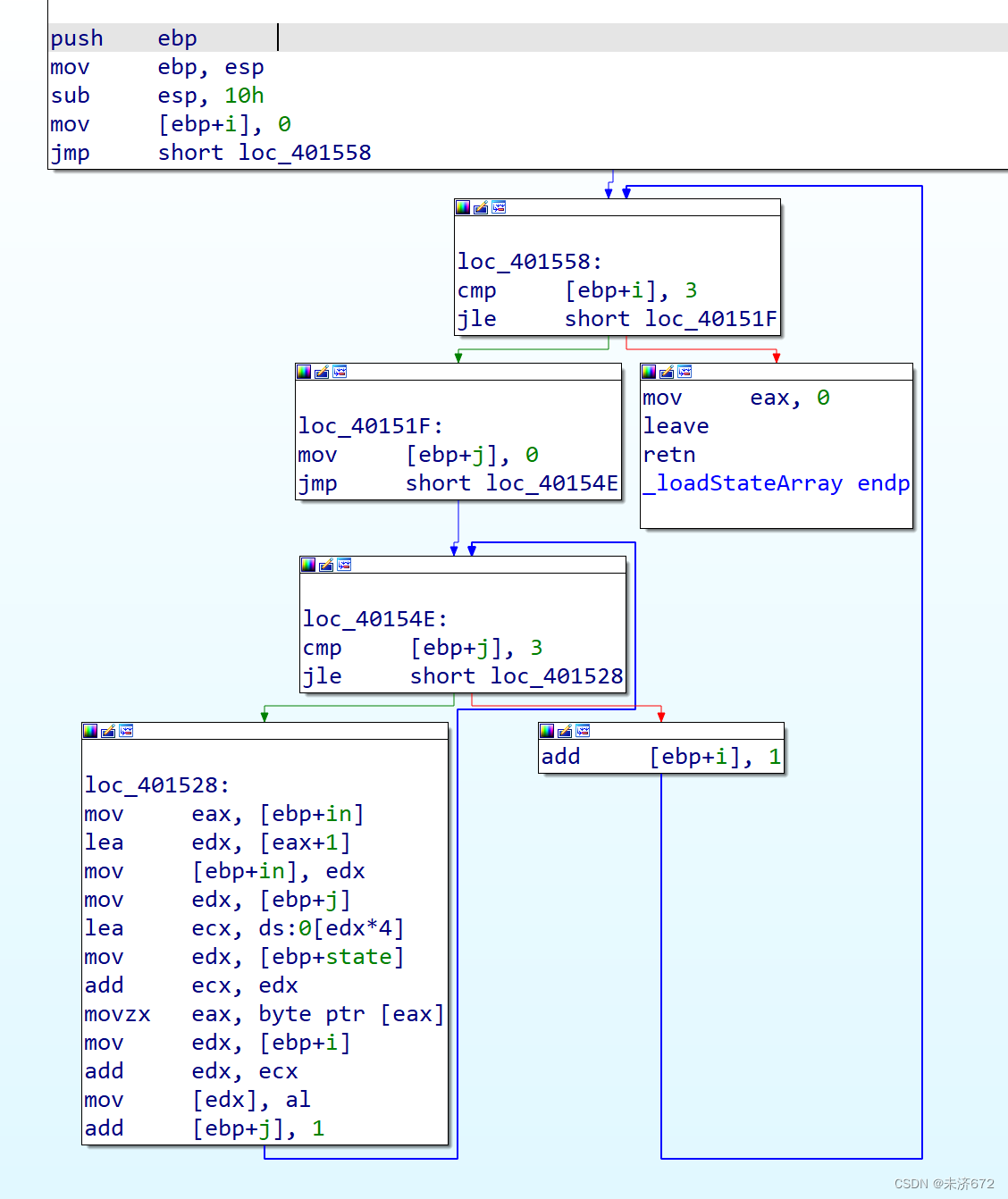
请添加图片描述
返回上级函数。

压入轮密钥rk（由数据初始化可知rk就是扩展加密密钥），压入状态矩阵，开始轮密钥加。
请添加图片描述

2.2.3 轮密钥加函数分析

轮密钥加过程是状态矩阵中的每1列和对应密钥的按位异或操作，如下图所示：
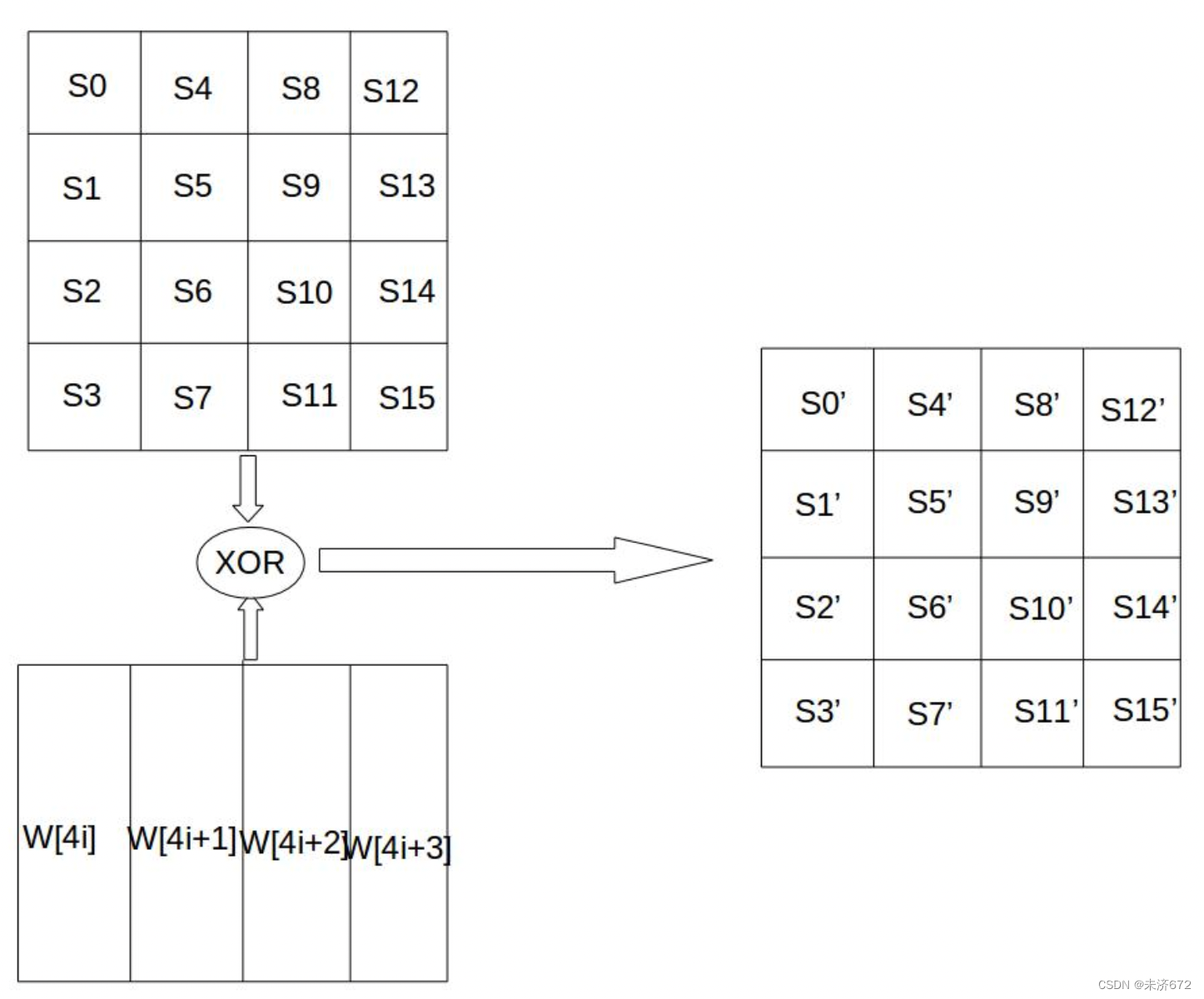
请添加图片描述
如下图所示部分是开始两层嵌套循环遍历状态矩阵的每个元素，i对应行、j对应列。

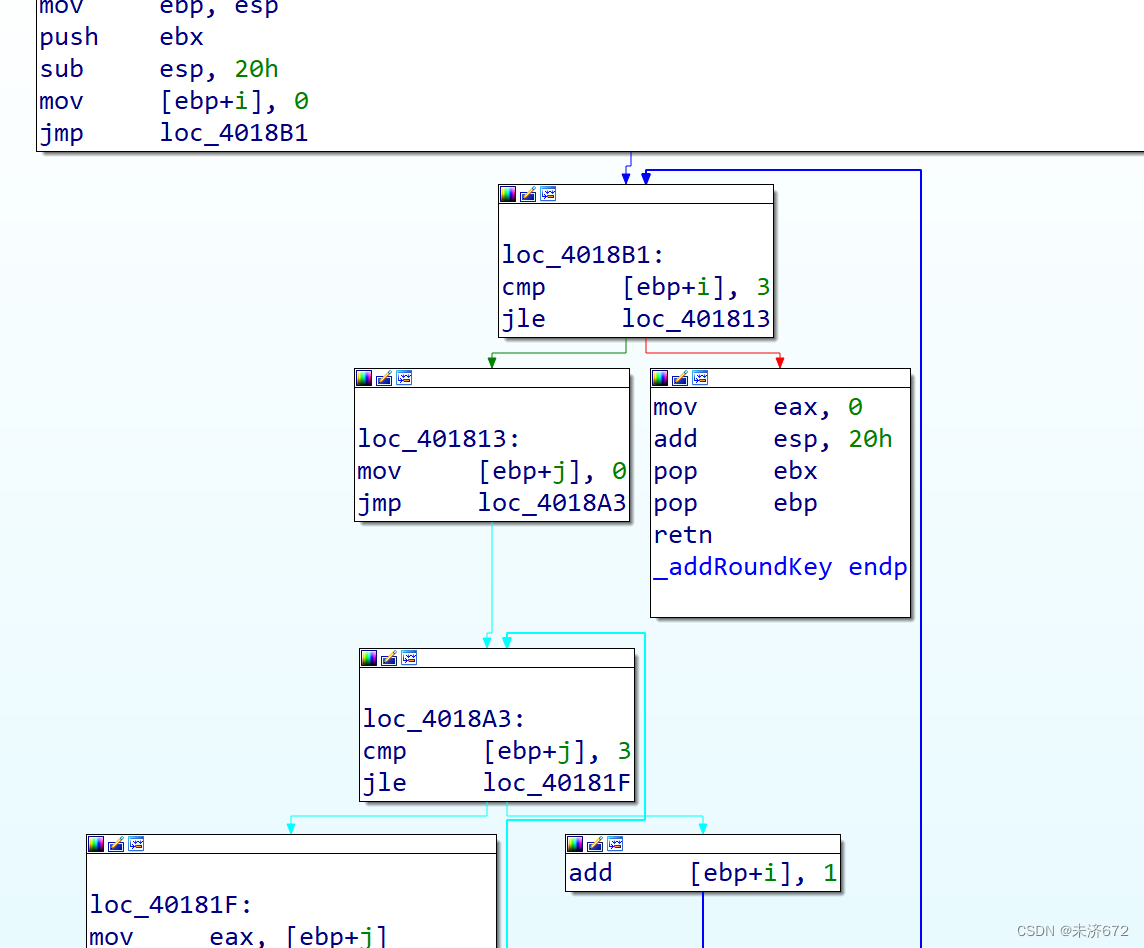
取对应列的密钥的对应部分（32位分成4组，0行对应高8位以此类推）放入ebx中，然后与ecx中的状态矩阵的对应元素异或后存回状态矩阵的对应位置上。
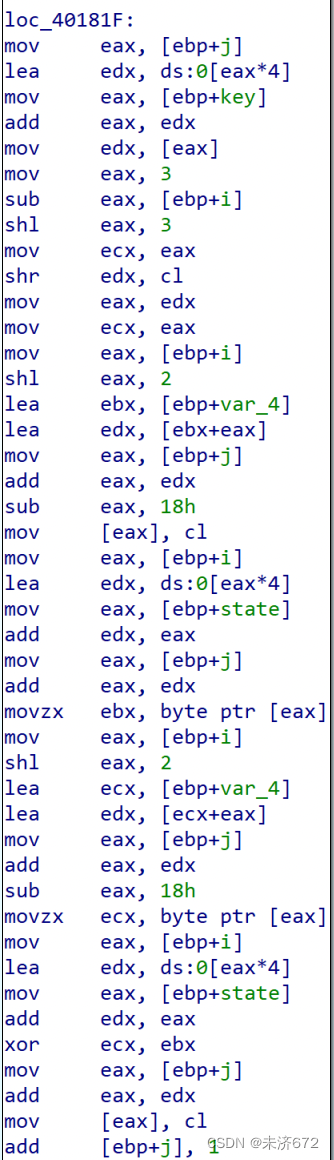
请添加图片描述
返回上级函数。

开启9轮并单独1轮的轮函数。首先压入密钥和状态矩阵进行字节代换。
请添加图片描述

2.2.4 字节代换函数分析

状态矩阵中的元素按照下面的方式映射为1个新的字节:把该字节的高4位作为行值，低4位作为列值，取出S盒中对应的行的元素作为输出。

此处与密钥扩展时的字节代换颇为相似，故此不做赘述。

返回上级函数。

压入状态矩阵开始行移位操作。

2.2.5 行移位函数分析

行移位是1个简单的左循环移位操作。当密钥⻓度为128比特时，状态矩阵的第0行左移0字节，第1行左移1字节，第2行左移2字节，第3行左移3字节，如下图所示：
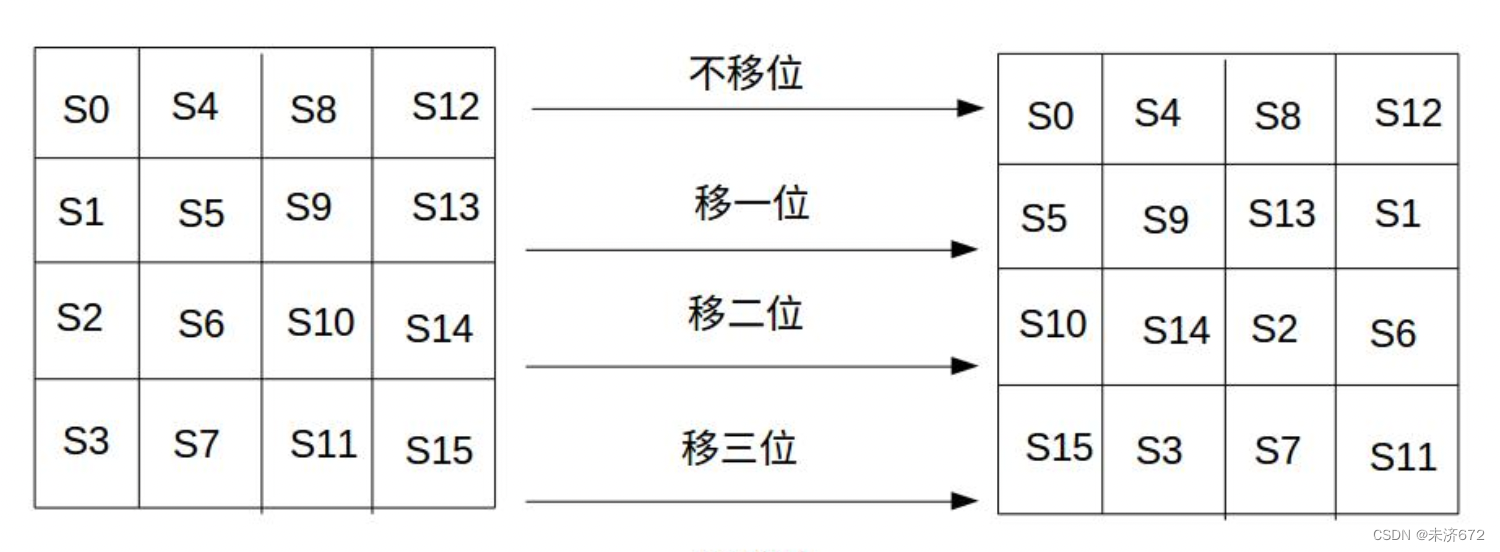
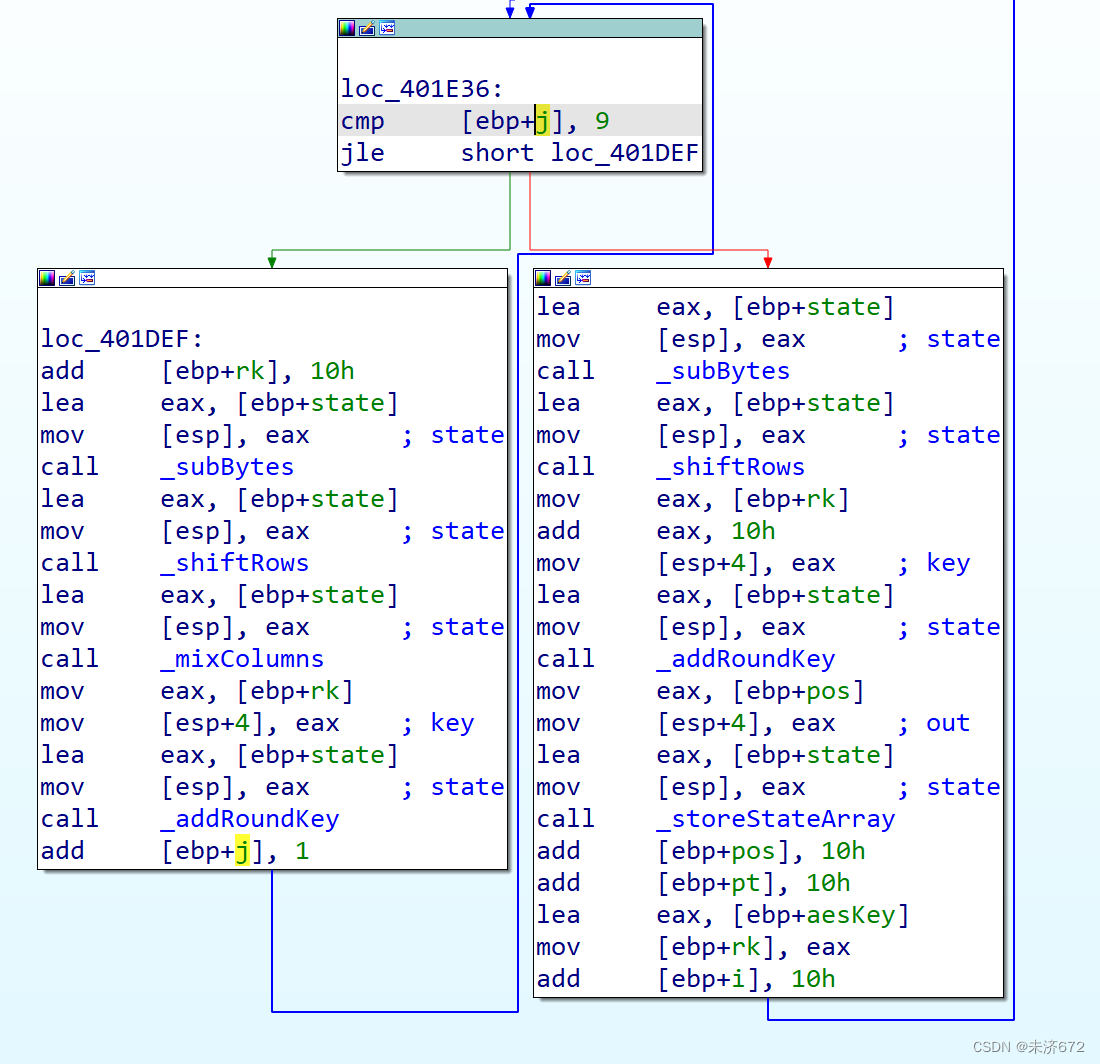
请添加图片描述
在汇编代码中整体上看是1个4轮的循环。

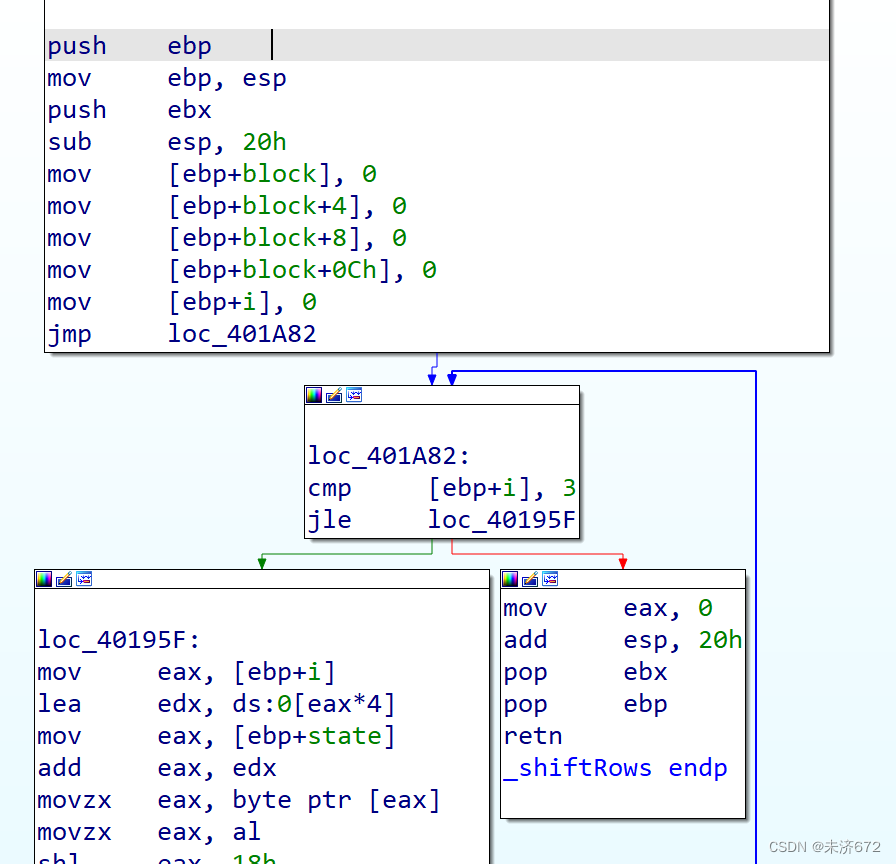
3个or之后（8位8位得拼4次），状态矩阵的1行就被载入到1个32位的变量（block）中。

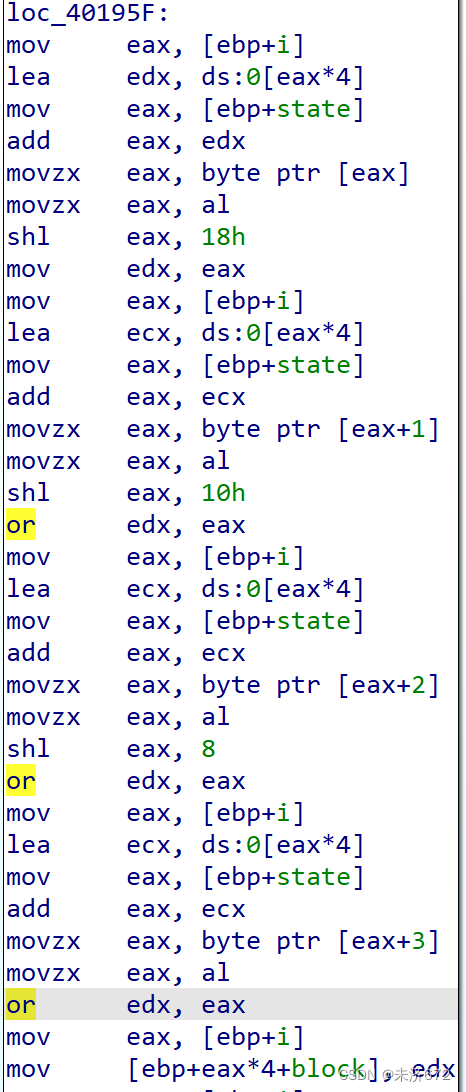
接下来重点关注左右移指令，左移3即*8，先对block中的值左移i*8位存入ebx，再对block右移(4-i)*8位存入eax，2者或运算就得到了对应行移位后的值。
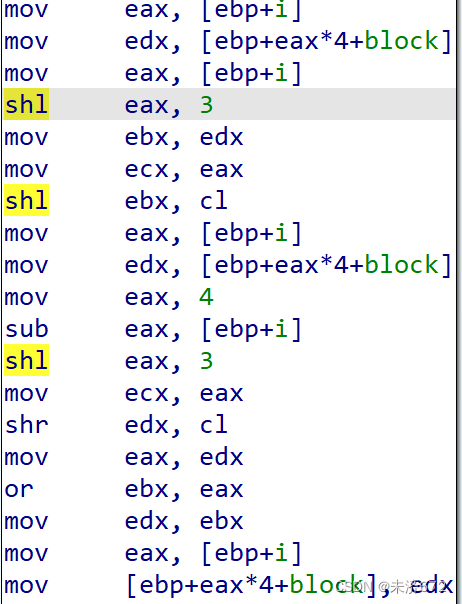
请添加图片描述
随后要将block中的值存回状态矩阵中。eax(+1,+2,+3)分别对应状态矩阵i行的0、1、2、3列，该部分将block中的4*8位右移回正常的8位中，并赋值到状态矩阵相应位置上。

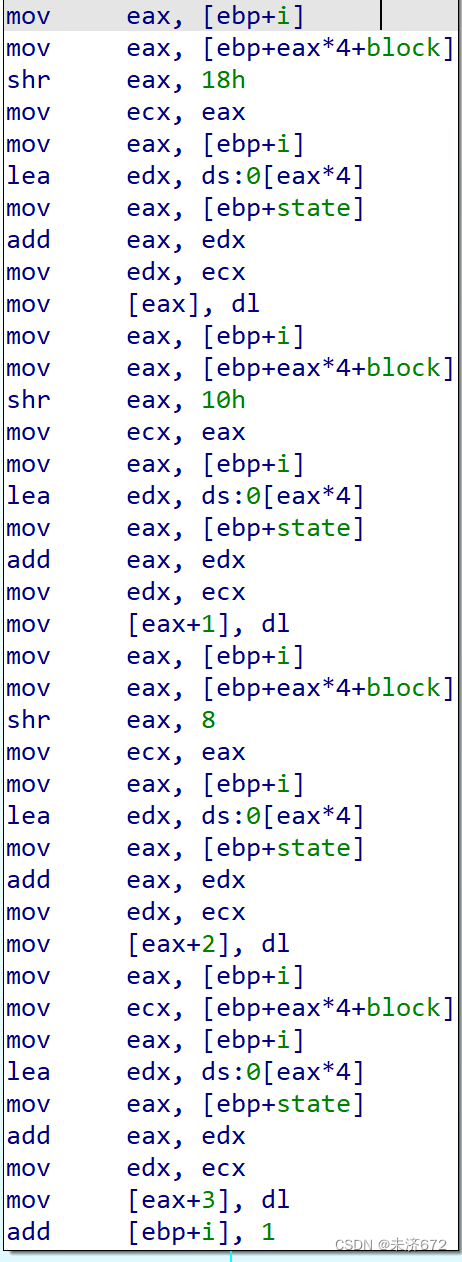
如此循环4轮即可完成行移位。

返回上级函数。

压入状态矩阵开始列混合。
请添加图片描述

2.2.6 列混合函数分析

列混合变换是通过矩阵相乘来实现的，经行移位后的状态矩阵与固定的矩阵相乘，得到混淆后的状态矩阵，如下图的公式所示：
请添加图片描述
状态矩阵中的第j列(0≤j≤3)的列混合可以表示为下图所示：

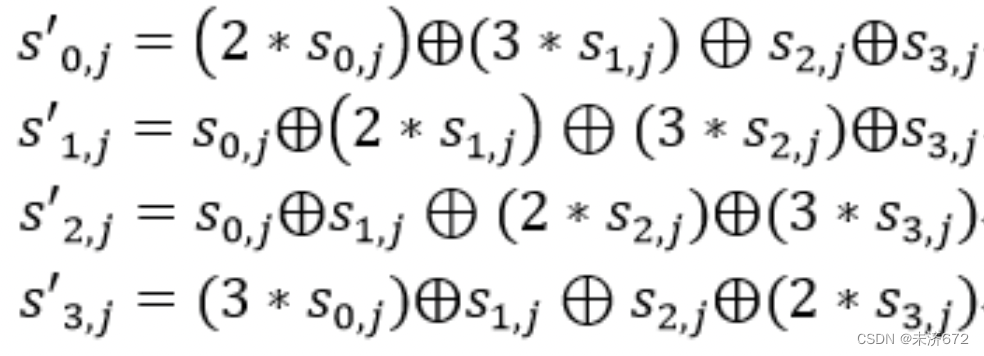
乘法和加法都是定义在基于 $GF(2^8)$ 上的2元运算，加法等价于两个字节的异或，乘法乘以(00000010)等价于左移1位(低位补0)后，再根据情况同(00011011)进行异或运算，设 $S_1 = (a_7 a_6 a_5 a_4 a_3 a_2 a_1 a_0)$ ，则 $02×S102\times S1$ 如下图所示：
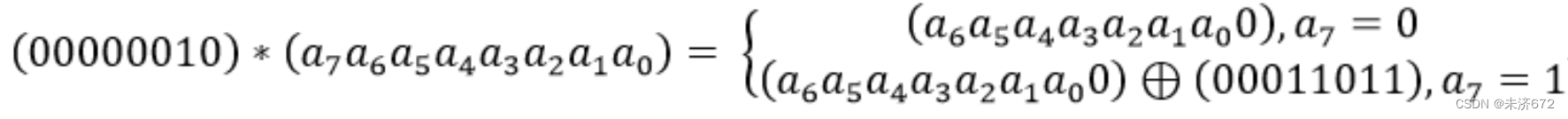
请添加图片描述
$(00000111)=(00000100)⊕(00000010)⊕(00000001)=(00000010)×(00000010)⊕(00000010)⊕(00000001)(00000111)=(00000100)\oplus(00000010)\oplus(00000001)=(00000010)\times(00000010)\oplus(00000010)\oplus(00000001)$

任意串都可以表示为02和01，因此只需要实现02的乘法即可。

该部分初始化阶段初始化了待乘矩阵M。该部分为两遍两层嵌套循环。第1遍先把状态矩阵完全复制给var_4-18h即tmp的位置上，构造1个一样的矩阵备用。
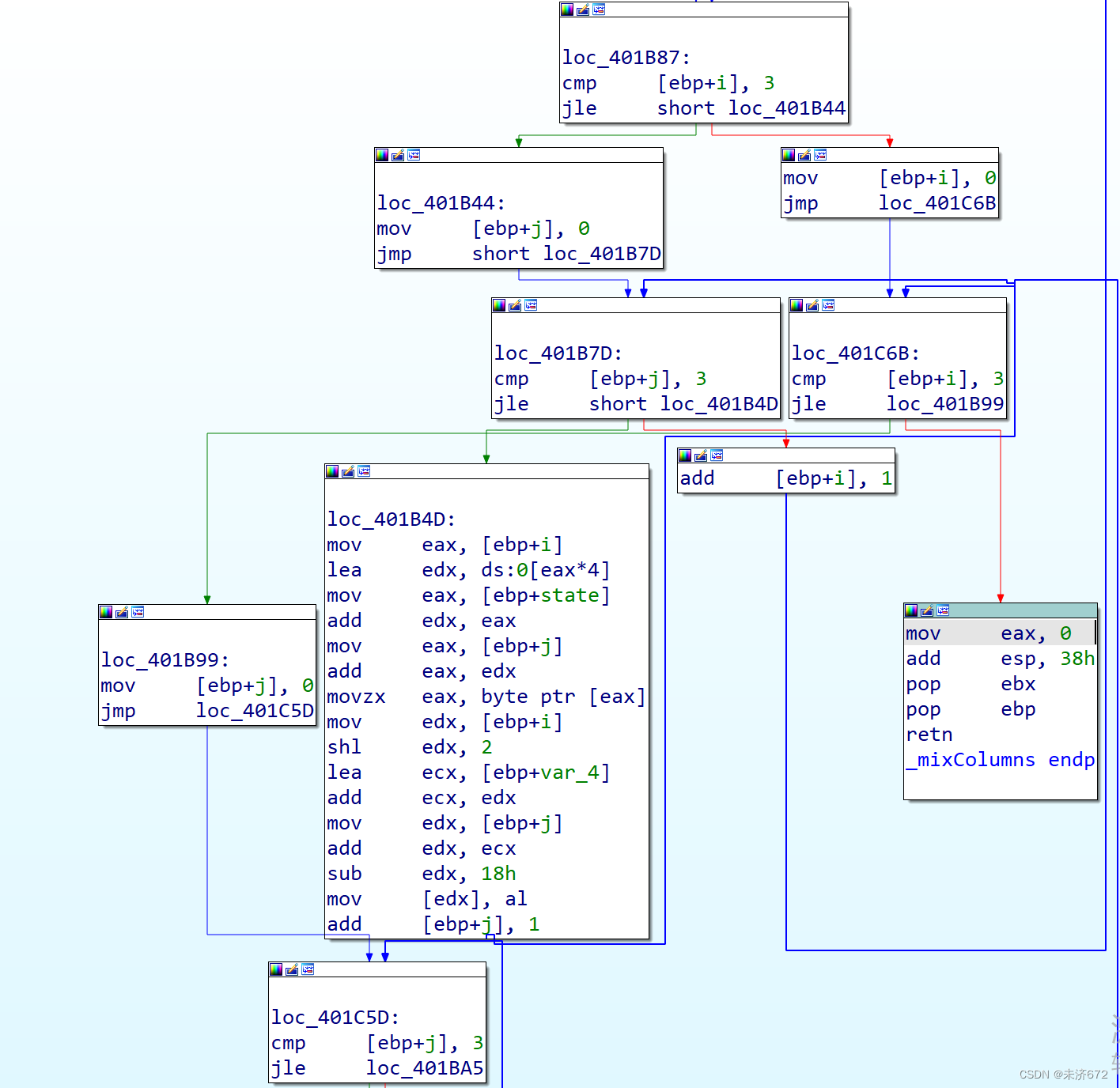
请添加图片描述
第2遍，观察整体结构，调用4次GMul函数，第1次将结果存入ebx，随后两次用结果与上次结果进行异或，最后1次异或完存入ecx，再将结果存入状态矩阵i行j列，完成矩阵乘法1步。

每次调用的参数都是edx和eax，主要关注这两个寄存器。以第1次调用为例，edx是tmp矩阵的0行j列，eax是M矩阵的i行0列，随后调用GMul函数。
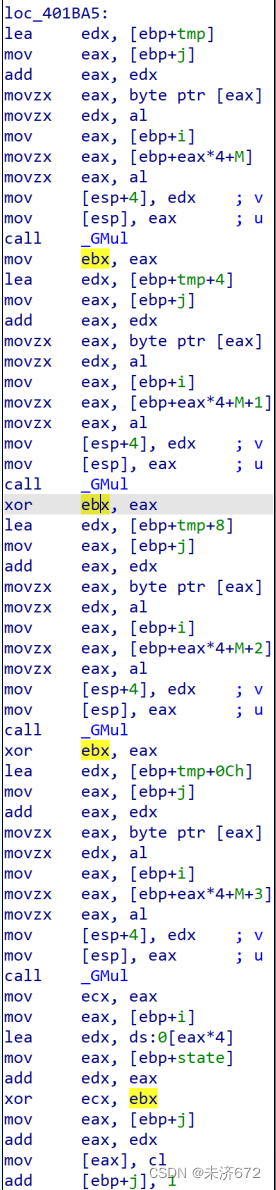
请添加图片描述
该函数是单层8次循环。取出u的最低位，如果有值则把v异或到p中，若v的最高位为1则v左移1位之后需要进行异或运算，完成后算u的第2位即u右移1位之后的第1位。此时v已经左移了1位，再用p和v异或时就计算的是 $p=p⊕(00000010)×vp=p\oplus(00000010)\times v$ ，每1轮若需要对不可约多项式进行异或，下1轮计算的就是 $p=p⊕(00000010)×v⊕(00011011)p=p\oplus(00000010)\times v\oplus(00011011)$ ，相当于延迟1轮计算，同时因为M矩阵中的元素都比较小不会出现第8轮仍需要异或不可约多项式的情况。
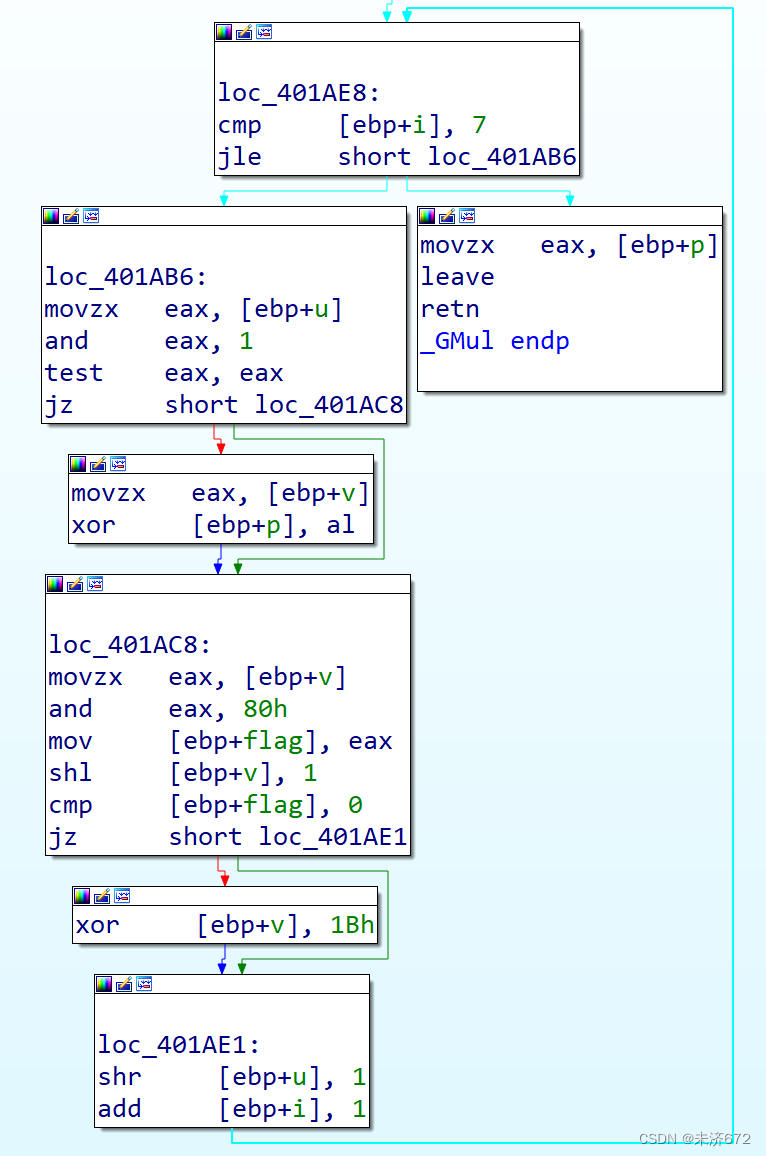
请添加图片描述
如此完成列混合，返回上级函数。

压入rk和状态矩阵进行轮密钥加，其过程与密钥扩展时的相似，不再赘述。
请添加图片描述
9轮之后的第10轮没有列混合，其余相似，不再赘述。

压入结果数组的位置指针和状态矩阵，进行状态矩阵存储，保存结果。
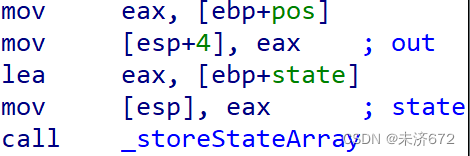
请添加图片描述

2.2.7 状态矩阵存储函数分析

该部分较为简单，是将状态矩阵中的元素复制到out数组的当前指针位置处。
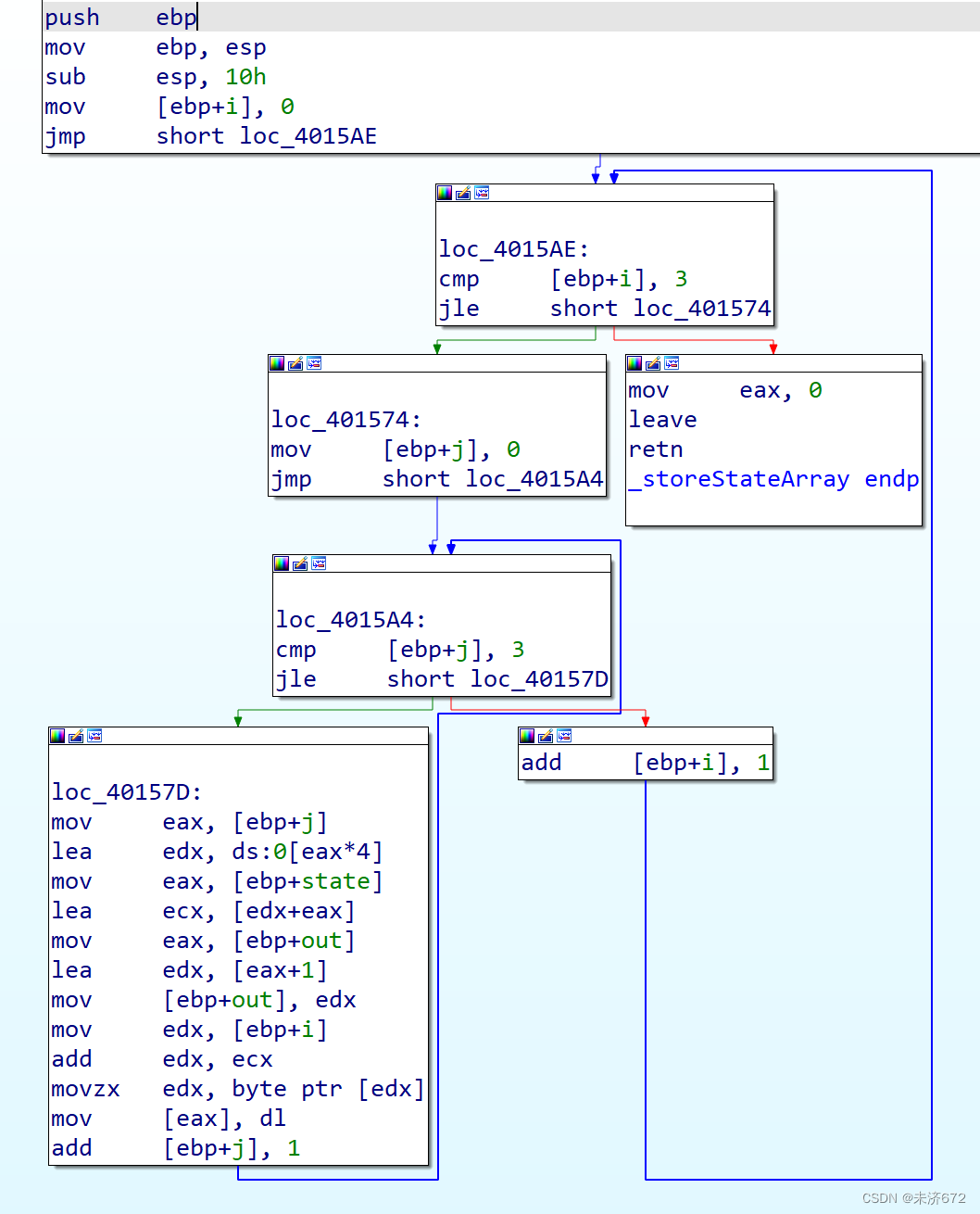
请添加图片描述
返回上级函数。

加密函数的最后1部分是对程序状态的更新，结果数组的位置指针前进16字节，明文数组的指针前进16字节，rk刷新为aes加密密钥的头部，开始下1分组的加密。
请添加图片描述
至此AESEnc逆向分析结束。

//AESEnc.c
//gcc -m32 -g AESEnc.c -o AESE.exe
#include <stdio.h>
#include <string.h>
#define BLOCKSIZE 16

#define LOAD32H(x, y) \
  do { (x) = ((unsigned int)((y)[0] & 0xff)<<24) | ((unsigned int)((y)[1] & 0xff)<<16) | \
             ((unsigned int)((y)[2] & 0xff)<<8)  | ((unsigned int)((y)[3] & 0xff));} while(0)

#define STORE32H(x, y) \
  do { (y)[0] = (unsigned char)(((x)>>24) & 0xff); (y)[1] = (unsigned char)(((x)>>16) & 0xff);   \
       (y)[2] = (unsigned char)(((x)>>8) & 0xff); (y)[3] = (unsigned char)((x) & 0xff); } while(0)

/* extract a byte */
#define BYTE(x, n) (((x) >> (8 * (n))) & 0xff)

/* used for keyExpansion */
#define MIX(x) (((S[BYTE(x, 2)] << 24) & 0xff000000) ^ ((S[BYTE(x, 1)] << 16) & 0xff0000) ^ \
                ((S[BYTE(x, 0)] << 8) & 0xff00) ^ (S[BYTE(x, 3)] & 0xff))

#define ROF32(x, n)  (((x) << (n)) | ((x) >> (32-(n))))

#define ROR32(x, n)  (((x) >> (n)) | ((x) << (32-(n))))

/* for 128-bit blocks, Rijndael never uses more than 10 rcon values */
static const unsigned int rcon[10] = {
        0x01000000UL, 0x02000000UL, 0x04000000UL, 0x08000000UL, 0x10000000UL,
        0x20000000UL, 0x40000000UL, 0x80000000UL, 0x1B000000UL, 0x36000000UL
};

unsigned char S[256] = {
        0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
        0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
        0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
        0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
        0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
        0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
        0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
        0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
        0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
        0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
        0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
        0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
        0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
        0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
        0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
        0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16
};

unsigned char inv_S[256] = {
        0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5, 0x38, 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB,
        0x7C, 0xE3, 0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, 0x34, 0x8E, 0x43, 0x44, 0xC4, 0xDE, 0xE9, 0xCB,
        0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D, 0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E,
        0x08, 0x2E, 0xA1, 0x66, 0x28, 0xD9, 0x24, 0xB2, 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B, 0xD1, 0x25,
        0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xD4, 0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92,
        0x6C, 0x70, 0x48, 0x50, 0xFD, 0xED, 0xB9, 0xDA, 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D, 0x84,
        0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, 0xF7, 0xE4, 0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06,
        0xD0, 0x2C, 0x1E, 0x8F, 0xCA, 0x3F, 0x0F, 0x02, 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B,
        0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, 0x97, 0xF2, 0xCF, 0xCE, 0xF0, 0xB4, 0xE6, 0x73,
        0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD, 0x35, 0x85, 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E,
        0x47, 0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, 0x6F, 0xB7, 0x62, 0x0E, 0xAA, 0x18, 0xBE, 0x1B,
        0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79, 0x20, 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4,
        0x1F, 0xDD, 0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, 0xB1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xEC, 0x5F,
        0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D, 0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF,
        0xA0, 0xE0, 0x3B, 0x4D, 0xAE, 0x2A, 0xF5, 0xB0, 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53, 0x99, 0x61,
        0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, 0xE1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D
};

typedef struct{
    unsigned int eK[44], dK[44];    // encKey, decKey
    int Nr; // 10 rounds
}AesKey;

/* copy in[16] to state[4][4] */
int loadStateArray(unsigned char (*state)[4], const unsigned char *in) {
    int i;
    int j;
    for (i = 0; i < 4; ++i) {
        for (j = 0; j < 4; ++j) {
            state[j][i] = *in++;
        }
    }
    return 0;
}

/* copy state[4][4] to out[16] */
int storeStateArray(unsigned char (*state)[4], unsigned char *out) {
    int i;
    int j;
    for (i = 0; i < 4; ++i) {
        for (j = 0; j < 4; ++j) {
            *out++ = state[j][i];
        }
    }
    return 0;
}

int keyExpansion(const unsigned char *key, unsigned int keyLen, AesKey *aesKey) {
    int i;
    int j;
    unsigned int *w;
    unsigned int *v;
    if (NULL == key || NULL == aesKey){
        printf("keyExpansion param is NULL\n");
        return -1;
    }

    if (keyLen != 16){
        printf("keyExpansion keyLen = %d, Not support.\n", keyLen);
        return -1;
    }

    w = aesKey->eK;
    v = aesKey->dK;

    /* keyLen is 16 Bytes, generate unsigned int W[44]. */

    /* W[0-3] */
    for (i = 0; i < 4; ++i) {
        LOAD32H(w[i], key + 4*i);
    }

    /* W[4-43] */
    for (i = 0; i < 10; ++i) {
        w[4] = w[0] ^ MIX(w[3]) ^ rcon[i];
        w[5] = w[1] ^ w[4];
        w[6] = w[2] ^ w[5];
        w[7] = w[3] ^ w[6];
        w += 4;
    }

    w = aesKey->eK+44 - 4;
    for (j = 0; j < 11; ++j) {

        for (i = 0; i < 4; ++i) {
            v[i] = w[i];
        }
        w -= 4;
        v += 4;
    }

    return 0;
}

int addRoundKey(unsigned char (*state)[4], const unsigned int *key) {
    int i;
    int j;
    unsigned char k[4][4];

    /* i: row, j: col */
    for (i = 0; i < 4; ++i) {
        for (j = 0; j < 4; ++j) {
            k[i][j] = (unsigned char) BYTE(key[j], 3 - i);  /* copy uint32 key[4] to uint8 k[4][4] */
            state[i][j] ^= k[i][j];
        }
    }

    return 0;
}

int subBytes(unsigned char (*state)[4]) {
    /* i: row, j: col */
    int i;
    int j;
    for (i = 0; i < 4; ++i) {
        for (j = 0; j < 4; ++j) {
            state[i][j] = S[state[i][j]];
        }
    }

    return 0;
}

int shiftRows(unsigned char (*state)[4]) {
    int i;
    unsigned int block[4] = {0};

    /* i: row */
    for (i = 0; i < 4; ++i) {
        LOAD32H(block[i], state[i]);
        block[i] = ROF32(block[i], 8*i);
        STORE32H(block[i], state[i]);
    }

    return 0;
}

/* Galois Field (256) Multiplication of two Bytes */
unsigned char GMul(unsigned char u, unsigned char v) {
    int i;
    int j;
	int flag;
    unsigned char p = 0;

    for (i = 0; i < 8; ++i) {
        if (u & 0x01) {    //
            p ^= v;
        }

        flag = (v & 0x80);
        v <<= 1;
        if (flag) {
            v ^= 0x1B; /* x^8 + x^4 + x^3 + x + 1 */
        }

        u >>= 1;
    }

    return p;
}

int mixColumns(unsigned char (*state)[4]) {
    int i;
    int j;
    unsigned char tmp[4][4];
    unsigned char M[4][4] = {{0x02, 0x03, 0x01, 0x01},
                       {0x01, 0x02, 0x03, 0x01},
                       {0x01, 0x01, 0x02, 0x03},
                       {0x03, 0x01, 0x01, 0x02}};

    /* copy state[4][4] to tmp[4][4] */
    for (i = 0; i < 4; ++i) {
        for (j = 0; j < 4; ++j){
            tmp[i][j] = state[i][j];
        }
    }

    for (i = 0; i < 4; ++i) {
        for (j = 0; j < 4; ++j) {
            state[i][j] = GMul(M[i][0], tmp[0][j]) ^ GMul(M[i][1], tmp[1][j])
                        ^ GMul(M[i][2], tmp[2][j]) ^ GMul(M[i][3], tmp[3][j]);
        }
    }

    return 0;
}

int aesEncrypt(const unsigned char *key, unsigned int keyLen, const unsigned char *pt, unsigned char *ct, unsigned int len) {
    int i;
    int j;
    AesKey aesKey;
    unsigned char *pos = ct;
    const unsigned int *rk = aesKey.eK;
    unsigned char out[BLOCKSIZE] = {0};
    unsigned char actualKey[16] = {0};
    unsigned char state[4][4] = {0};

    if (NULL == key || NULL == pt || NULL == ct){
        printf("param err.\n");
        return -1;
    }

    if (keyLen > 16){
        printf("keyLen must be 16.\n");
        return -1;
    }

    if (len % BLOCKSIZE){
        printf("inLen is invalid.\n");
        return -1;
    }

    memcpy(actualKey, key, keyLen);
    keyExpansion(actualKey, 16, &aesKey);

    for (i = 0; i < len; i += BLOCKSIZE) {

        loadStateArray(state, pt);
        addRoundKey(state, rk);

        for (j = 1; j < 10; ++j) {
            rk += 4;
            subBytes(state);
            shiftRows(state);
            mixColumns(state);
            addRoundKey(state, rk);
        }

        subBytes(state);
        shiftRows(state);
        addRoundKey(state, rk+4);

        storeStateArray(state, pos);

        pos += BLOCKSIZE;
        pt += BLOCKSIZE;
        rk = aesKey.eK;
    }
    return 0;
}

int main() {
    int i;
    int j;	
    const unsigned char key[]="1234567890123456";
    unsigned char data[40] = "abcdefghijklmnopqrstuvwxyzabcdef";
	unsigned char cipher[32] = {0xfc,0xad,0x71,0x5b,0xd7,0x3b,0x5c,0xb0,0x48,0x8f,0x84,0x0f,0x3b,0xad,0x78,0x89,0xd0,0xe7,0x09,0xd0,0xff,0xd3,0x8c,0x6d,0xfe,0xc5,0x5c,0xcb,0x9f,0x47,0x5b,0x01};
	unsigned char ct[32] = {0};

	printf("Please provide the Flag:");
	scanf("%s",data);

    aesEncrypt(key, 16, data, ct, 32);

    for(i = 0; i < 32; ++i){
		if (cipher[i] != ct[i]){
			printf("You really don't know!!!!!\n");
			break;
		}
	}
    
    if(i==32){
		printf("You really know!!!!!\n");
	}

    return 0;
}