学习笔记|Pytorch使用教程14(损失函数(一))

学习笔记|Pytorch使用教程14

本学习笔记主要摘自“深度之眼”，做一个总结，方便查阅。
使用Pytorch版本为1.2

• 损失函数概念
• 交叉熵损失函数
• NLL/BCE/BCEWithLogits Loss
• 作业

一.损失函数概念

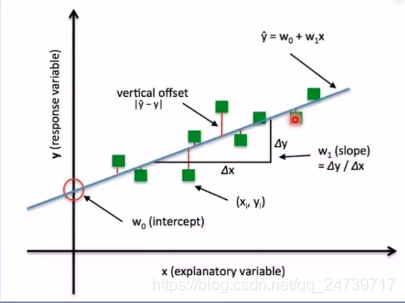
损失函数:衡量模型输出与真实标签的差异

• 损失函数(Loss Function) :
  $$Loss=f\left(y^{\wedge },y\right)$$
• 代价函数(Cost Function) :
  $$\cos t=\frac{1}{N}\sum _i^{N}f\left(y_i^{\wedge },y_i\right)$$
• 目标函数(Objective Function) :
  $$Obj=Cost+Regularization$$
  
  size_average和reduce被舍弃。

测试代码：
完整代码见
学习笔记|Pytorch使用教程09(模型创建与nn.Module)

......
# 参数设置
......
# ============================ step 1/5 数据 ============================
......

# 构建MyDataset实例
......
# 构建DataLoder
......
# ============================ step 2/5 模型 ============================
......
# ============================ step 3/5 损失函数 ============================
loss_functoin = nn.CrossEntropyLoss()                                                   # 选择损失函数
# ============================ step 4/5 优化器 ============================
 # 选择优化器
 # 设置学习率下降策略
 .......
# ============================ step 5/5 训练 ============================
......
for epoch in range(MAX_EPOCH):
......
    for i, data in enumerate(train_loader):
        # forward
		......
        # backward
        optimizer.zero_grad()
        loss = loss_functoin(outputs, labels)
        loss.backward()
        # update weights
		......
        # 统计分类情况
        # 打印训练信息
		......

在loss_functoin = nn.CrossEntropyLoss()和loss = loss_functoin(outputs, labels)处设置断点，进行debug了解其机制。
首先debug到loss_functoin = nn.CrossEntropyLoss()，并进入(step into)。

class CrossEntropyLoss(_WeightedLoss):
    r"""This criterion combines :func:`nn.LogSoftmax` and 
	.......
    Examples::

        >>> loss = nn.CrossEntropyLoss()
        >>> input = torch.randn(3, 5, requires_grad=True)
        >>> target = torch.empty(3, dtype=torch.long).random_(5)
        >>> output = loss(input, target)
        >>> output.backward()
    """
    __constants__ = ['weight', 'ignore_index', 'reduction']

    def __init__(self, weight=None, size_average=None, ignore_index=-100,
                 reduce=None, reduction='mean'):
        super(CrossEntropyLoss, self).__init__(weight, size_average, reduce, reduction)
        self.ignore_index = ignore_index

    def forward(self, input, target):
        return F.cross_entropy(input, target, weight=self.weight,
                               ignore_index=self.ignore_index, reduction=self.reduction)

进入(step into):super(CrossEntropyLoss, self).__init__(weight, size_average, reduce, reduction)

class _WeightedLoss(_Loss):
    def __init__(self, weight=None, size_average=None, reduce=None, reduction='mean'):
        super(_WeightedLoss, self).__init__(size_average, reduce, reduction)
        self.register_buffer('weight', weight)

_WeightedLoss继承于 _Loss
进行进入(step into):super(_WeightedLoss, self).__init__(size_average, reduce, reduction)

class _Loss(Module):
    def __init__(self, size_average=None, reduce=None, reduction='mean'):
        super(_Loss, self).__init__()
        if size_average is not None or reduce is not None:
            self.reduction = _Reduction.legacy_get_string(size_average, reduce)
        else:
            self.reduction = reduction

_Loss 又继承于 Module。
接下来继续debug，进入:loss_functoin = nn.CrossEntropyLoss()

进入:result = self.forward(*input, **kwargs)

这里调用了F.cross_entropy，在该处进入(step into)
进入cross_entropy中，对reduction进行判断并进行计算。

二.交叉熵损失函数

交叉熵=信息熵+相对熵
$H(P,Q)=D_{KL}(P,Q)+H(P)$

• 交叉熵:衡量两个分布的相似度。
  H ( P , Q ) = − ∑ i = 1 N P ( x i ) log