队列与堆:学习队列思想及堆排序思想,并完成leetcode上的返回滑动口中的最大值(239)
打卡方式:提交队列与堆学习心得笔记 +LeetCode提交结果与代码
一。队列:
1.队列特点
队列是一种特殊的数据结构,不同于栈这种特殊的数据结构只能在一个位置(栈顶)删除和插入数据,队列可以在队首插入数据和队尾删除数据,而且队列具有“先进先出”的特点。
2.队列类型
首先根据队列长度是否确定进行划分,这里类似于顺序表和链表。
1.顺序队列:当队列长度确定的时候,采用顺序存储
(1)静态顺序队列:使用数组存储队列
(2)动态顺序队列:使用动态分配的指针
2.链式队列:当队列长度不确定时使用,使用链式存储
由于队列在顺序存储上的不足(删除一个元素需要将第一个元素之后的元素都往前移动,此时的复杂度是O(n)),所以引出了循环队列(复杂度为O(1))。
3.基于数组的循环队列:
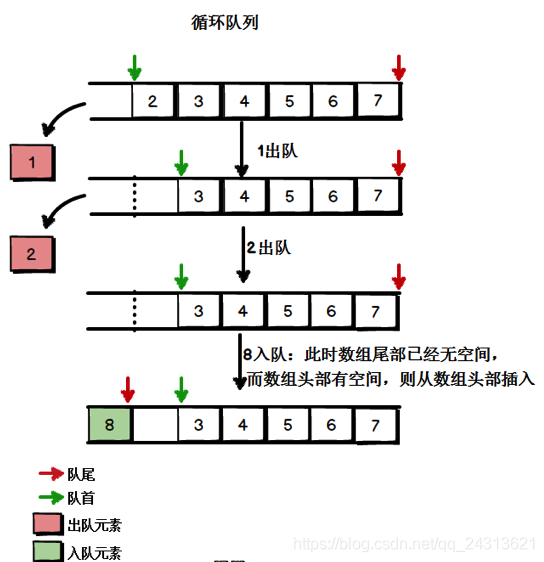
所谓的循环队列,可以把数组看出一个首尾相连的圆环。
删除元素时将队首标志往后移动,比如删除元素1时下图中的绿色箭头往后移动了一个位置。
添加元素时若数组尾部已经没有空间,则考虑数组头部的空间是否空闲。
如果是,则在数组头部进行插入。比如下图中入队元素8,数组尾部没有空间,所以从数组头部插入,插入到了第一个位置。
3.队列操作:
共有两个操作:入队和出队。
例如我们有一个存储整型元素的队列,我们依次入队:{1,2,3}
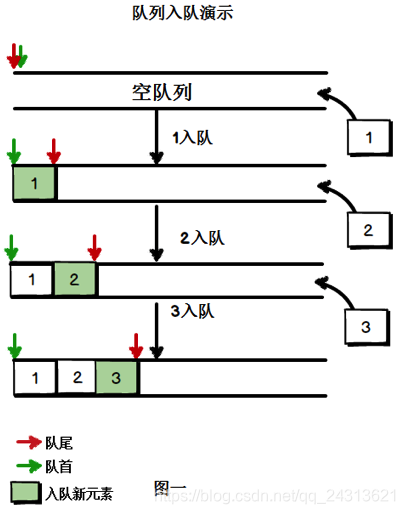
添加元素时,元素只能从队尾一端进入队列,也即是2只能跟在1后面,3只能跟在2后面。
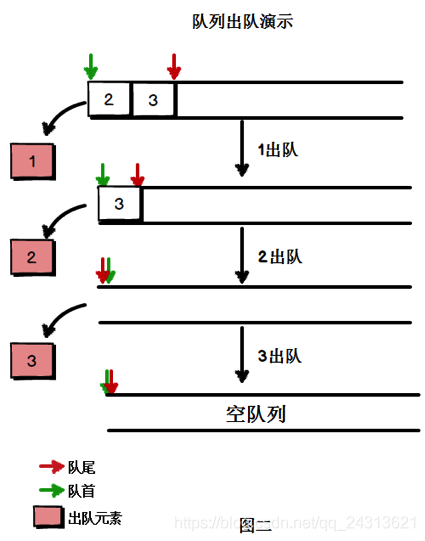
如果队列中的元素要出队:
LeetCode 239. Sliding Window Maximum
Given an array nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position. Return the max sliding window.
Example:
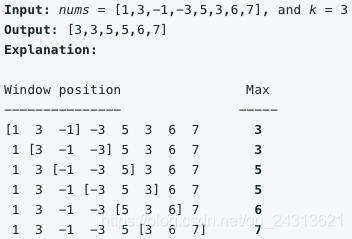
题目意思就是有一个固定大小k的滑动窗口,每滑动一个位置求一次窗口内元素的最大值。
求解思想:利用一个双向队列,每次元素进入队列,比已有的元素进行比较,如果比已有元素小,就弹出,否则弹出已有元素。
举个例子(k=3):
1.入队1 [1]
2.再入队[1 3],比较大小,出队1,[3]
3.入队-1,[3 -1],比较大小,出队-1,[3],输出3
从第k+1次开始,每入队比较过之后,都输出一个最大值。
完整代码:
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
vector<int> f;
int n = nums.size();
//如果输入数据为空,或者k大于数据长度,就返回null
if(n == 0 || k > n)
return f;
deque<int> que;
for(int i = 0; i < n; i++)
{
//如果队列非空
if(!que.empty())
{
//如果此时队首元素超出窗口范围值,就弹出
if(i >= que.front()+k)
que.pop_front();
//如果队列非空且新加入的值等于或者等于队列中的元素,就弹出队列中的元素
while(!que.empty() && nums[i] >= nums[que.back()])
que.pop_back();
}
//如果队列为空,直接加入数据
que.push_back(i);
//如果索引+1大于等于k时,说明此时已经到达窗口范围值,需要输出最大值
if(i+1 >= k)
f.push_back(nums[que.front()]);
}
return f;
}
};二。堆排序
这部分内容摘自参考资料2。
1.概念
堆是一棵顺序存储的完全二叉树。
其中每个结点的关键字都不大于其孩子结点的关键字,这样的堆称为小根堆。
其中每个结点的关键字都不小于其孩子结点的关键字,这样的堆称为大根堆。
举例来说,对于n个元素的序列{R0, R1, ... , Rn}当且仅当满足下列关系之一时,称之为堆:
(1) Ri <= R2i+1 且 Ri <= R2i+2 (小根堆)
(2) Ri >= R2i+1 且 Ri >= R2i+2 (大根堆)
其中i=1,2,…,n/2向下取整;
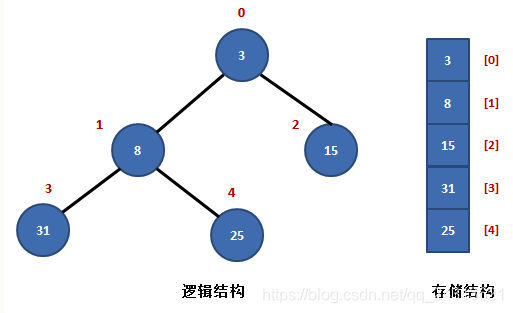
如上图所示,序列R{3, 8, 15, 31, 25}是一个典型的小根堆。
堆中有两个父结点,元素3和元素8。
元素3在数组中以R[0]表示,它的左孩子结点是R[1],右孩子结点是R[2]。
元素8在数组中以R[1]表示,它的左孩子结点是R[3],右孩子结点是R[4],它的父结点是R[0]。可以看出,它们满足以下规律:
设当前元素在数组中以R[i]表示,那么,
(1) 它的左孩子结点是:R[2*i+1];
(2) 它的右孩子结点是:R[2*i+2];
(3) 它的父结点是:R[(i-1)/2];
(4) R[i] <= R[2*i+1] 且 R[i] <= R[2i+2]。
2.堆排序思想
首先,按堆的定义将数组R[0..n]调整为堆(这个过程称为创建初始堆),交换R[0]和R[n];
然后,将R[0..n-1]调整为堆,交换R[0]和R[n-1];
如此反复,直到交换了R[0]和R[1]为止。
以上思想可归纳为两个操作:
(1)根据初始数组去构造初始堆(构建一个完全二叉树,保证所有的父结点都比它的孩子结点数值大)。
(2)每次交换第一个和最后一个元素,输出最后一个元素(最大值),然后把剩下元素重新调整为大根堆。
当输出完最后一个元素后,这个数组已经是按照从小到大的顺序排列了。
先通过详细的实例图来看一下,如何构建初始堆。
设有一个无序序列 { 1, 3, 4, 5, 2, 6, 9, 7, 8, 0 }。
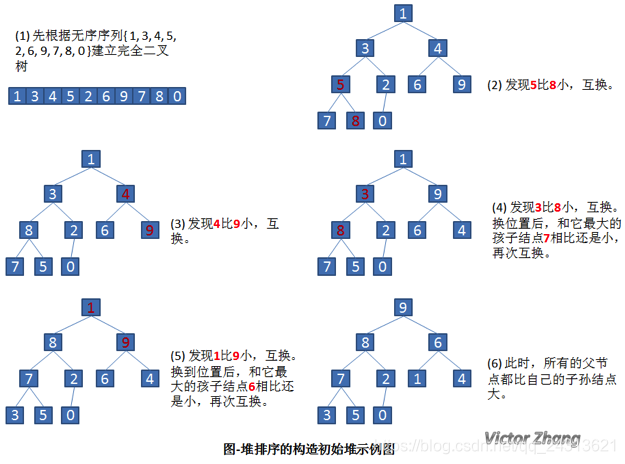
构造了初始堆后,我们来看一下完整的堆排序处理:
还是针对前面提到的无序序列 { 1, 3, 4, 5, 2, 6, 9, 7, 8, 0 } 来加以说明。

参考资料:
2.排序六 堆排序





 本文深入探讨了队列和堆排序的基本概念、特性及应用。详细解析了队列的不同类型,包括顺序队列和链式队列,以及循环队列的实现方式。同时,阐述了堆排序的原理,包括小根堆和大根堆的概念,以及堆排序的具体步骤。并通过LeetCode题目的解答,展示了队列和堆排序的实际应用。
本文深入探讨了队列和堆排序的基本概念、特性及应用。详细解析了队列的不同类型,包括顺序队列和链式队列,以及循环队列的实现方式。同时,阐述了堆排序的原理,包括小根堆和大根堆的概念,以及堆排序的具体步骤。并通过LeetCode题目的解答,展示了队列和堆排序的实际应用。
















 788
788

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








