矩阵（一）

特殊矩阵

对称矩阵

 

三角矩阵：

假设数组b用来存储矩阵的元素，则矩阵元素的下标(i,j)与该元素在数组b中的存储位置k之间有如下关系：

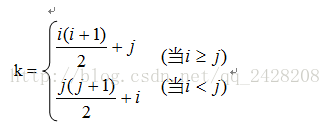
稀疏矩阵

包含大量零元素的矩阵称为稀疏矩阵，其经常出现在以下领域：大规模集成电路设计、电力输配系统、图像处理、城市规划等。
对此可只存储非零元素，对这些非零元素可采取顺序或链接的方式存储。

稀疏矩阵的顺序表示：三元组表示法
矩阵的元素aij可以看成一个三元组<i,j,v>,i为行号，j为列号，v为元素值
三元组表示的C语言描述：

 

#define MaxSize 101
typedef int T;
typedef struct term//三元组类型
{
	int Row,Col;
	T Value;
}Term;
typedef struct triples//三元组表类型
{
	int  Rows,Cols,NonZeros;//矩阵的行数、列数、非零元素的个数
	Term Elements[MaxSize];
}Triples;
typedef Triples SparseMatrix;

除了三元组表示方式外，还有伪地址方式，非零元素按行优先顺序的存储在一位数组中，元素aij在一位数组中的下标。
Loc(aij) = i*n+j; (0<=i<=n-1.0<=j<=n-1)

稀疏矩阵的转置

 

如图为一稀疏矩阵，其三元组表为：
（1）普通法：
若采用普通的二维数组来存储时，求解矩阵Am*n的转置矩阵An*m的程序段：

 

		for(int i=0;i<m;i++)
			for(int j=0;j<m;j++)
				B[j][i] = A[i][j];

 

 

 

 

其时间复杂度为O(m*n)
（2）方法一：

 

 

 

 

将原数组中的每一个元素的行列交换得到数组B，然后在数组B中，将所有元素按行号进行排列，这里矩阵的转置时间取决于排序时间，典型的排序算法的时间复杂度为O(t^2)或O(t lb t),t为非零元素的个数
（3）方法二：

对数组A 进行n次扫描，第一遍取矩阵A的第0列元素，得到转置矩阵B的第0行元素，第i遍取出A的第i-1 列元素，得到B的第i-1 行元素，依次存入数组B中，此方法的时间复杂度为O(n*t)t为非0元素个数
（4）快速转置算法：

快速转置算法通过适当增加存储空间达到节省时间的目的。
快速转置算法使用数组k，k[i]为矩阵A中第i列的第一个非零元素在数组B中存放的位置。数组k的长度为矩阵的列数n。
例：k[3] = 5 表示矩阵A的第三列的第一个非零元素a03 = 22 在数组B的下标为5。为了得到数组k需要知道它的长度，于是用另外一个数组num保存矩阵A中个列的非0元素的个数
例：num[2]存放矩阵A的第2列非0元素的个数，即转置矩阵B第2行非零元素的个数。
数组num的值有以下语句求得：

 

for(int i=0;i<Col;i++)
        num[i] = 0; //初始化为0
for(i = 0;i <nonzeros;i++)//对所有非0元素
	num[a.Elements[i].Col]++;//将对应行的个数加一

当数组num的值已经计算出，则数组k可以简单地由以下递推公式计算

 

 

	k[0] = 0;                   //B的第0行的第一个非0元素始终存放在下标为0的位置
	k[i] = k[i-1] + num[i-1];  (1<= i <n)

见下列语句：

 

k[0] = 0;
for(int i=1;i<cols;i++)
	k[i] = k[i-1] + num[i-1]  (1<= i <n)

 

 

 

对于原数组，计算num和k的结果见下表：

有了数组k只需对A扫描一次即可完成转置。完成这项工作的程序段如下：

 

 

 

 

 

	有了数组k只需对A扫描一次即可完成转置。完成这项工作的程序段如下：
		for(int i=0;i<nonzeros;i++)
		{
			j=k[a.Elements[i].Col]++;//获取元素的下标，加一定位到数组B的具体位置，若第二次出现一个与第一在同一行的元素，
	//因第一次操作完后,下标志加了一，因此将存在第一个元素的后面。
			b.Elements[j].Row = a.Elements[i].Col;//分别复制数据
			b.Elements[j].Col = a.Elements[i].Row;
			b.Elements[j].Value = a.Elements[i].Value;
		}

 

下面给出稀疏矩阵的快速转置程序：

 

 

 

		Triples	Tripose(Triples a)//三元表a为参数
		{
			Triples b;//创建三元表b为转置矩阵
			int num[MAX_COL];//存放每一列的非零元素的个数
			int k[MAX_COL];
			int i,j;
			int cols = a.Cols;
			int nonzeros = a.NonZeros;
			b.Rows = a.Cols;//行、列转置
			b.Cols = a.Rows;
			b.NonZeros = a.NonZeros;
			if(nonzeros>0)
			{
				for(i = 1;i<cols;i++)
					k[i] = k[i-1]+num[i-1];//计算每一列第一个元素的位置
				for(i = 0;i<nonzeros;i++)
				{
					j=k[a.Elements[i].Col]++;
					b.Elements[j].Row = a.Elements[i].Col;//分别复制数据
					b.Elements[j].Col = a.Elements[i].Row;
					b.Elements[j].Value = a.Elements[i].Value;
				}
			}
			return b;
		}

其时间复杂度为O(Cols+NonZeros);