什么是跳跃表？

一、什么是跳跃表？

          跳跃表(Skip List)是一种基于【有序链表】的扩展，简称【跳表】。

          其实就是使用【关键节点】作为【索引】的一种结构。

          怎样能更快查找到一个【有序链表】的某一节点呢？

            可以利用类似【索引】的思想，提取出【链表】中的【部分关键节点】

                比如：
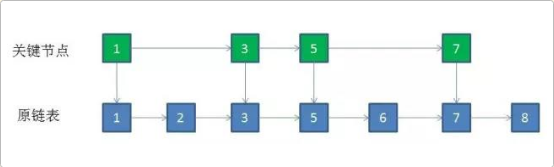
                  ①.  给定一个长度是7的有序链表，节点值依次是1->2->3->5->6->7->8
                         那么我们可以取出所有值为【奇数的节点】作为关键点。

                

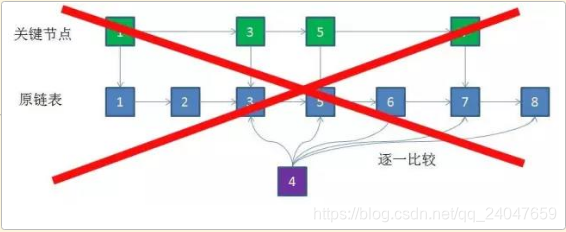
               ②. 此时如果要插入一个值是4的新节点，不再需要和原节点8,7,6,5,3逐一比较，只需要比较关键节点7,5,3

              

             

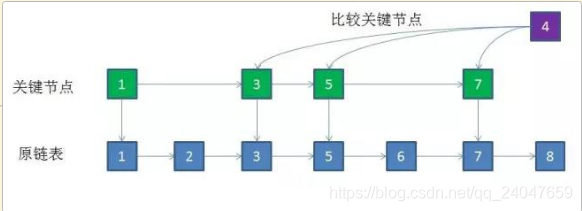
            ③. 确定了【新节点在关键节点中的位置】(3和5之间)，就可以【回到原链表】，迅速定位到对应的位置插入(同样是3和5之间)

             

             

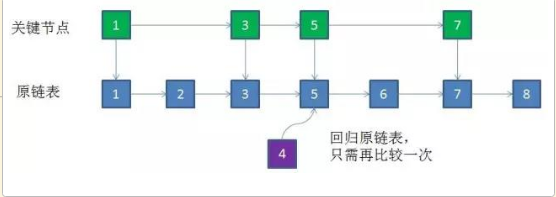
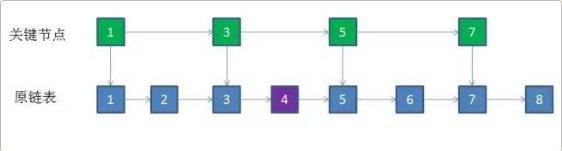
            这样一个插入就完成了。

 

二、多层关键节点多层索引

   当然，既然已经提取出了【一层关键节点】作为【索引】，那么可以进一步提取索引，提出一层索引的索引

   

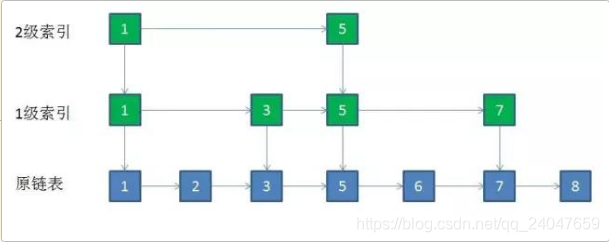
   有了2级索引之后，新的节点可以先和2级索引比较，确定大体范围；

   然后再和1级索引比较；

   最后再回到原链表，找到并插入对应位置。

   

层级极限是什么？

当节点足够多的时候，不止能提出2层索引，还可以向更高层次提取，保证每一层是上一层节点数的【一半】

  至于提取的【极限】，则是：

    同一层只有【两个节点】的时候，因为一个节点没有比较的意义。

 这样的【多层链表】结构，就是所谓的【跳跃表】

 

三、怎么从新节点当中选取一部分提到上一层（抛硬币法）？

       当大量的新节点通过逐层比较，最终插入到原链表之后，上层的索引节点会渐渐变得不够用。
       这时候需要从新节点当中选取一部分提到上一层。

       使用【抛硬币】。

         也就是随机决定新节点是否提拔，每次向上提拔一层的几率是50%

   举个例子：

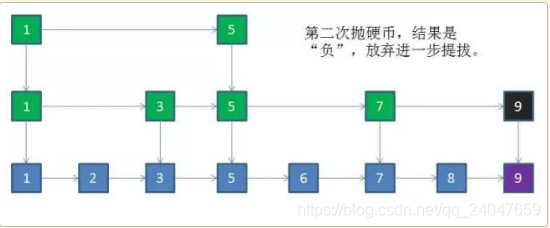
        借用上面的例子，假如值为9新节点插入原链表

        

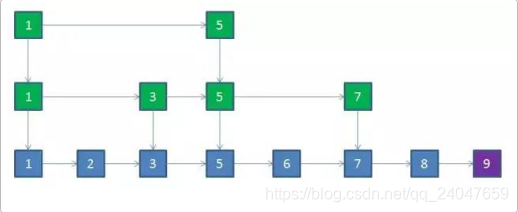
       1） 第一次抛硬币，结果是"正"，因此把节点9提拔到上一层索引

        

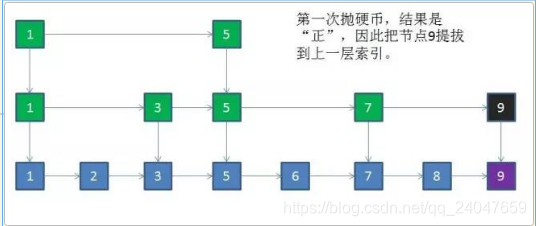
       2） 第二次抛硬币，结果是"负"，放弃进一步提拔

        

 

为什么要用抛硬币?

      ①.  因为跳跃表删除和添加的节点是不可预测的，很难用一种有效的算法来保证跳表的索引部分始终均匀。

      ②.  随机抛硬币的方法虽然不能保证索引绝对均匀分布，却可以让大体趋于均匀

 

四、跳跃表【插入节点】的流程？

          1. 新节点和各层索引节点逐一比较，确定原链表的插入位置。O（logN）

          2. 把新节点插入到原链表。O（1）

          3. 利用抛硬币的随机方式，决定新节点是否提升为上一级索引。
              结果为“正”则提升并继续抛硬币，结果为“负”则停止。O（logN）

 

五、跳跃表【删除节点】的流程？

           删除操作比较简单

            1） 只要在【索引层】找到【要删除的节点】，然后顺藤摸瓜，【删除每一层的相同节点】即可。

            2） 如果某一层索引在删除后只剩下一个节点，那么整个一层就可以干掉了。
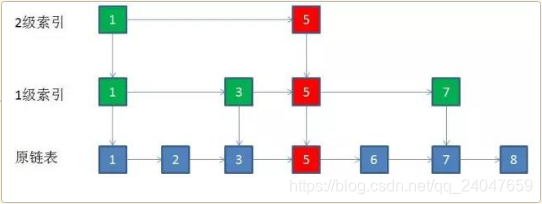
                   还用上面的例子，如果要删除的节点值是5:

                

                

    删除节点的步骤：

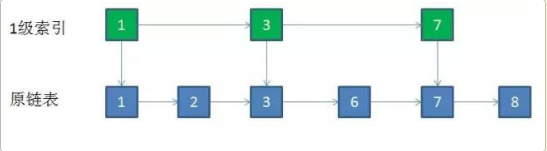
        1. 自上而下，查找第一次出现节点的索引，并逐层找到每一层对应的节点。O(logN)

        2. 删除每一层查找到的节点，如果该层只剩下1个节点，删除整个一层（原链表除外）。O(logN)

 

六、跳跃表和二叉查找树的区别？

           跳跃表的优点：

               维持【结构平衡】的成本比较低，完全依靠【随机】

           二叉查找树：

               在多次插入、删除后，需要rebalance来重新调整结构平衡

 

七、跳跃表的实际运用

         1. Redis当中的Sorted-set这种【有序集合】，正是对跳跃表的改进和应用。

         2. 对于关系型数据库如何维护有序的记录集合呢？

              使用的是B+树