算法-二叉树的最近公共祖先

1、二叉树的最近公共祖先（2节点）

236. 二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

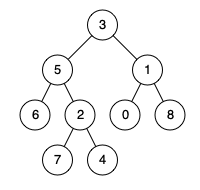
例如，给定如下二叉树:  root = [3,5,1,6,2,0,8,null,null,7,4]

示例 1:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
 

说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉树中。

题目描述是非常清晰的，题目已经给我们条件，说节点一定存在给我们的二叉树里面，那我们可以在此基础上实现我们的算法。

我们可以想象，有两种情况：
1、两个节点的具有一个和他们自身不相等的父节点
2、两个节点中一个节点为另一个节点的父亲

基于以上条件，我们可以得到下面的结论

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root==null||p==root||q==root){
            return root;
        }
        //left和right一定是p或q或者null,一定不可能同时为null,除非pq都为null
        //如果都不为null，那么说明满足我们上面提到的情况1
        //如果有一个为null，那么满足情况2
        TreeNode left=lowestCommonAncestor(root.left,p,q);
        TreeNode right=lowestCommonAncestor(root.right,p,q);
        if(left!=null&&right!=null){
            return root;
        }
        return left!=null?left:right;
    }

详情看注释，这里不多做解释了

2、二叉树的最近公共祖先（3节点）

三个节点的二叉树公共祖先问题和2节点甚至n节点逻辑是完全一样的,非常简单，不再赘述。

    public TreeNode threeNodesHead(TreeNode root,TreeNode n1, TreeNode n2, TreeNode n3){
        return originNode(root,n1,n2,n3);
    }

    public TreeNode originNode(TreeNode root,TreeNode n1,TreeNode n2,TreeNode n3){
        if(root==null){
            return null;
        }
        if(n1==root||n2==root||n3==root){
            return root;
        }
        TreeNode left=originNode(root.left,n1,n2,n3);
        TreeNode right=originNode(root.right,n1,n2,n3);
        if(left!=null&&right!=null){
            return root;
        }
        if(left!=null){
            return left;
        }
        if(right!=null){
            return right;
        }
        return null;

    }