神经网络基础-线性模型_线性神经网络模型-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_23334761/article/details/123630029

本文深入探讨了线性模型在分类问题中的应用，从二分类到多分类，详细介绍了逻辑回归和softmax函数。通过实例展示了如何使用逻辑回归解决二分类问题，并通过梯度下降法进行参数更新。接着，解释了softmax在多分类任务中的作用，解释了softmax函数的理论和计算过程，并给出了实际应用案例。最后，简述了感知器算法及其在二分类问题中的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

10. 用softmax回归进行MNIST数据集的手写数字识别（实战）

线性模型（line model），之前已经接触过很多次。它主要是通过把样本的特征线性组合，然后在进行一个预测。线性模型反应了机器学习非常重要的一个思路：从错误中学到知识或经验，关键是正确的认识错误。

之前都是预测一个实值，或找到一个概率。总而言之都是找到一个值（预测或回归问题）。接下来，都是总结线性模型在分类上的应用。

1. 分类介绍

怎么把实值转换成一个离散的值（离散的值能表示具体的分类，如判断是猫还是狗，结果是1就是猫，0就是狗。）？我们需要引入一个决策函数（有时称为符号函数），如把f(x)作为自变量进过决策函数g(f(x))运算后就转换为一个离散值。

如：狗，猫，猴概率值是{0.2,0.9,0.1}，那么可以认为输出就是猫。

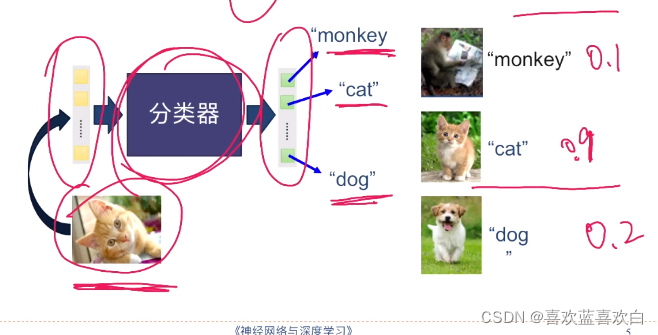
让原来的线性模型输出一个非线性的输出。

2. 线性模型处理分类问题

之前的实战的内容都是特征只有一种的，即在二维坐标中的一条线。

但在真正分类的过程中，要识别出一个物品，我们需要依据他很多的特征，即X (X1,X2……)，把这个X经过线性模型输出的结果在经过几个决策函数，就可以得到一个分类的结果。

如图，x有很多个特征，b是偏执项。右图是二者相加得到的增广权重矩阵乘以增广特征矩阵，后将结果经过一个决策函数，最后得到一个结果。最后在经过分类器可以得到分类结果。

3. 二分类问题

下图右图，连坐标轴表示的是两个特征。假如是一分类就是一个坐标轴。

二分类就是要找到一条线y = w1*x1 + w2*x2 + b = 0，把两个特征给分开，下图右图就是把实心圆和空心圆分开。

怎么分呢？把样本点带进y中，最后得出结果若小于0，则是线下方的值，大于0则是上方的值，这里的决策函数就是左图所示。最后得到了两种离散值，这就是决策函数的功能。

为什么把结果带进去之后大于0小于0就能直接分类呢？我们可以通过求距离公式，距离公式的分子就是w1**2 + w2**2再开根号，也就是其二范式。其>0最终就是取决于分子是否大于0.

4. 多分类

一对其余：用一条直线将一个与其他所有分开，假如有c个特征的话，我们需要c条直线将其分开。但缺点就是，会有少数点不能区分是哪一类。

一对一：用c（i，j）表示类别i和类别j之间的区分，这样根据排列组合，我们需要c（c-1）/ 2条直线将其分开。

“argmax”方式：一种改进的一堆其余的方式，C个特征共需要C个判别式，求出每个样本是所有类别的可能性，最终取最大可能的类别。

5. 从概率角度看待分类问题

5.1. 多元线性回归进行分类产生的问题

无法处理极度离群的样本，如下图红圈内的差本应该出现在直线右边，但此时彻底的在左边。

无法处理非线性的分类：如下图圈和差。

5.2. 从概率角度解决分类问题

为了解决线性函数不适合进行分类的问题，我们引入非线性函数g来预测表情的后验概率 $p(y = c|x)$ ,即f(x;w) = x时，标签取c的概率是多少。p既然是概率那么一定就是一个[0,1]的值。

则我们可以想象，我们引入的非线性函数一定是一个可以把f（x；w）挤压到[0,1]的函数。

接下来举例介绍1个这样的非线性函数：

Logistics函数（sigmoid函数）： $\frac{1}{1+e^{-x}}$ 。（这是s族函数中的一种，用得比较多。）

在sigmoid的基础上，在f（x；w） = x时，目标类别y = 1的概率又可以表示为：

模型有了，那么学习准则用什么表示呢？

真实值：
预测值：

怎么衡量这两个条件分布之间的差异呢？这时就可以利用交叉熵了！

6. 交叉熵

如以上所讲，在机器学习中，交叉熵就是用来评价目标概率和真实概率之间的差异。在信息论中，交叉熵用来衡量一个随机事件的不确定性。

在理解交叉熵之前，我们理解一下信息量的概念

6.1. 信息量的数学期望就是熵

比如说，我们听说了两件事，狗咬人，第二件事，人咬狗。在可能性上，狗咬人的可能性比人咬狗的时间可能性大。在信息量上，我们认为狗咬人不算是什么特别的事，人们之前就知道了，获取的信息量可以认为很低，但是若发生了人咬狗事件，则认为信息量很大。因此，我们认为，可能性和信息量刚好呈一个反比。

那么我们现在假设X是一个试验，x1离散型的随机变量是实验X中的一个可能事件，设x发生的概率为p(x) = p(X = x)，那么信息量可以为 $I(x_{1}) = -log(p(x))$ ，但x = 1时，ln(x) = 0即信息量为0，但x = 0时，信息量无限趋近于正无穷。

则熵是什么呢？一个事情可能有很多种可能性，每种可能性都有一种给概率。（即分类类别都有一种概率），则每个时间的概率都可以求出来一个信息量，而熵就是所有信息量的数学期望。

特殊的对于二分类问题， $H(x) = -plog(p) + (-(1-p)log(1-p))$

6.2. 相对熵

相对熵有时称为KL散度。我们真实值是：p(x),预测值是Q(x)，但预测值的离真实值还有一定距离时，我们需要增加信息量，来让Q(x)无限接近于p(x)，直到我们可以认为Q == P。KL散度就是描述Q和P接近程度的一个概念。 $D_{KL} = \sum plog(\frac{p}{q}) = \sum plog(p)-\sum plog(q)$ ，KL散度越小则认为P和Q差距较小，因为但他们越接近时，他们的比值越接近1，则KL散度就越接近0。

KL散度的计算公式中第一个元素 $\sum plog(p)$ 就是每个事件的信息量*这个信息量的概率之和，即熵，是我们选取样本后知道的，确定的固定值，也就是说这个p是已知的。而在相对熵中我们不知道的就是q，即预测值。因此我们可以把KL散度的公式中的前半部分给移去，只留下后半部分， $H(p,q) = -\sum plog(q)$ 来描述p和q之间是否接近。而这个H(p,q)就是交叉熵！！！

交叉熵作为损失函数，模型在训练集上的风险函数为（二分类）：

这显然又是一个更新参数的过程，怎么更新呢？可以使用梯度下降法。

梯度为：

7. 逻辑回归（实战）

import numpy as np
import matplotlib.pyplot  as plt

#设置种子，让每次取得值都是一样的
np.random.seed(0)
Num = 100

# X(x1,x2) y 0/1
# y = 1
x_1 = np.random.normal(6,1,size=(Num))
x_2 = np.random.normal(3,1,size=(Num))
y = np.ones(Num)
c_1 = np.array([x_1,x_2,y])#如此直接拼接
c_1.shape
#np.random.normal(loc ,scale,size)
#loc:正态分布的均值，以此为中心，scale：标准差，标准差越大，曲线越矮胖，小则高瘦

x_1 = np.random.normal(3,1,size=(Num))
x_2 = np.random.normal(6,1,size=(Num))
y = np.zeros(Num)
c_0 = np.array([x_1,x_2,y])#如此直接拼接
c_0.shape

# 让表头是特征，行是样本
c_1 = c_1.T
c_0 = c_0.T

plt.scatter(c_1[:,0],c_1[:,1],marker='+')
plt.scatter(c_0[:,0],c_0[:,1])

#默认是按行拼接
All_date = np.concatenate((c_1,c_0))
All_date.shape

#一般是在第一维度打乱
np.random.shuffle(All_date)
train_date_X = All_date[:150,:2]
train_date_y = All_date[:150,-1]
text_date_X = All_date[150:,:2]
text_date_y = All_date[150:,-1]
train_date_X.shape,train_date_y.shape

# y = w*1xx1 + w2*x2 = 0
W = np.random.rand(2,1)
W

#w1 *x +w2*y = 0
plt.scatter(c_1[:,0],c_1[:,1],marker='+')
plt.scatter(c_0[:,0],c_0[:,1])
x = np.arange(10)
y = -(W[0]*x)/W[1]
plt.plot(x,y)

# 逻辑回归里，使用交叉熵作为损失函数
#定义损失函数,交叉熵
def cross_entropy(y,y_hat):
    return -np.mean( y*np.log(y_hat) + (1-y)*np.log(1-y_hat))

#y_hat = sigmoid(w*x)
def sigmoid(z):
    return 1./(1.+np.exp(-z))

#开始训练
lr = 0.001
loss_list = []
for i in range(1000):
    #计算交叉熵loss,监控一下变化情况，希望loss从大变小
    y_hat = sigmoid(np.dot(train_date_X,W))
    loss = cross_entropy(train_date_y,y_hat)
    loss_list.append(loss)
    # 计算梯度
    grad = - np.mean( (train_date_X*(train_date_y-y_hat.T).T),axis = 0 )#第一个维度上
    #在第一位都上求平均后（150，2） -> （1，2）
    #更新梯度 w参数
    W = W - (lr*grad).reshape(2,1)
    #输出
    if i%10 == 1:
        print("i: %d,loss:%f"%(i,loss))

#画图
plt.scatter(c_1[:,0],c_1[:,1],marker='+')
plt.scatter(c_0[:,0],c_0[:,1])
x = np.arange(10)
y = -(W[0]*x)/W[1]
plt.plot(x,y)

plt.plot(loss_list)

# 预测一下
# y_hat = w1*x1 +w2*x2 > 0，与真实值进行比较
y_hat = np.dot(W.T,text_date_X.T)
y_pred = np.array(y_hat>0,dtype=int).flatten()
a = text_date_y == y_pred

test_acc = np.sum(a)/a.size
test_acc

8. softmax

8.1. 理论

softmax是logistics在多分类上的推广，多分类的标签会有多个取值。而标签取c1的概率为：

分母为所有在训练集上标签取所有种类可能的概率之和。

模型确定了可以使用softmax，那风险函数呢？我们仍然可以使用交叉熵来判定。此时的交叉熵仍是所有信息量的数学期望（当然是哈哈哈，定义就是这样。）

优化方式仍然可以采用梯度下降法：

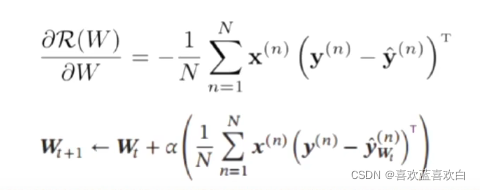
虽然书本上常看到的W权重和X特征向量都是增广向量，即加了那个偏执项。但是我们在计算的时候，往往会先计算W（参数）的偏导，即grad 再通过W = W - lr*grad的方式更新W。然后再求b的偏导，以同样的方式更新b的值。

学到这里里感觉softmax有点像贝叶斯公式，求的是一个后验概率。

8.2. softmax（实战）

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)
Num = 100

# y = 0
x_1 = np.random.normal(3,1,size = (Num)) # 3附近的满足高斯分布的点
x_2 = np.random.normal(-3,1,size = (Num)) # 3附近的反差为1的点
y = np.zeros(Num)
c_0 = np.array([x_1,x_2,y]) #[x1,x2]是特征,y是样本的预测值。

# y = 1
x_1 = np.random.normal(-3,1,size = (Num)) # -1附近的满足高斯分布的点
x_2 = np.random.normal(-3,1,size = (Num)) # 3附近的反差为1的点
y = np.ones(Num)
c_1 = np.array([x_1,x_2,y]) #[x1,x2]是特征,y是样本的预测值。

# y = 2
x_1 = np.random.normal(-3,1,size = (Num)) # -3附近的满足高斯分布的点
x_2 = np.random.normal(3,1,size = (Num)) # 3附近的反差为1的点
y = np.ones(Num)*2
c_2 = np.array([x_1,x_2,y]) #[x1,x2]是特征,y是样本的预测值。

# y = 3
x_1 = np.random.normal(3,1,size = (Num)) # 3附近的满足高斯分布的点
x_2 = np.random.normal(3,1,size = (Num)) # 3附近的反差为1的点
y = np.ones(Num)*3
c_3 = np.array([x_1,x_2,y]) #[x1,x2]是特征,y是样本的预测值。

c_0 = c_0.T
c_1 = c_1.T
c_2 = c_2.T
c_3 = c_3.T

plt.scatter(c_1[:,0],c_1[:,1],marker = '+')
plt.scatter(c_0[:,0],c_0[:,1],marker = '^')
plt.scatter(c_2[:,0],c_2[:,1],marker = '*')
plt.scatter(c_3[:,0],c_3[:,1])

All_data = np.concatenate( (c_0,c_1,c_2,c_3) )
All_data.shape

np.random.shuffle(All_data)

train_data_X = All_data[:300,:2]
train_data_y = All_data[:300,-1].reshape(300,1)
test_data_X = All_data[300:,:2]
test_data_y = All_data[300:,-1].reshape(100,1)

# 有四组W1，W2，则W的形状是4行2列
W = np.random.rand(4,2)

# 而b只有四个直线，因此只需定义一个1行4列的偏置值即可
bias = np.random.rand(1,4)

plt.scatter(c_1[:,0],c_1[:,1],marker = '+')
plt.scatter(c_0[:,0],c_0[:,1],marker = '^')
plt.scatter(c_2[:,0],c_2[:,1],marker = '*')
plt.scatter(c_3[:,0],c_3[:,1])
x = np.arange(-5,5)
y1 = -(W[0,0]*x + bias[0,0])/W[0,1]
y2 = -(W[1,0]*x + bias[0,1])/W[1,1]
y3 = -(W[2,0]*x + bias[0,2])/W[2,1]
y4 = -(W[3,0]*x + bias[0,3])/W[3,1]
plt.plot(x,y1,'b')
plt.plot(x,y2,'y')
plt.plot(x,y3,'g')
plt.plot(x,y4,'r')

# softmax(x) = e^x / sum(e^x)
#把所有实值转化为概率值
# 一维
def softmax1(z):
    return np.exp(z)/np.sum(np.exp(z))

a = np.array([1,2,3])
softmax1(a)

b = np.array([1,2,3,4,5,6,7,8,9]).reshape(3,3)
softmax1(b)

# 对于多行的z,即矩阵，希望softmax的分母是当前行的exp之和
def softmax(z):
    exp = np.exp(z)
    sum_exp = np.sum(np.exp(z),axis = 1,keepdims=True)
    return exp/sum_exp

softmax(b)

def one_hot(temp):
    one_list = np.zeros((len(temp),len(np.unique(temp) )))
    one_list[np.arange(len(temp)) , temp.astype(np.int).T] = 1
    return one_list

one_hot(train_data_y)

# 计算 y_hat
def compute_y_hat(W,X,b):
    return np.dot(X,W.T) + b

# 计算交叉熵
def cross_entropy(y,y_hat):
    return -(1/len(y))*np.sum(y*np.log(y_hat))

# w = w - lr*grad
lr = 0.01
loss_list = []
for i in range(10000):
    # 计算loss
    X = train_data_X
    y = one_hot(train_data_y)
    y_hat = softmax(compute_y_hat(W,X,bias))
    loss = cross_entropy(y,y_hat)
    loss_list.append(loss)
    # 计算梯度
    grad_w = (1/len(X))*np.dot(X.T,(y_hat - y))
    grad_b = (1/len(X))*np.sum(y_hat - y)
    #更新参数
    W = W - lr*grad_w.T
    bias = bias - lr*grad_b
    #输出
    if i%300 == 1:
        print("i: %d,loss : %f"%(i,loss))

plt.plot(loss_list)

plt.scatter(c_1[:,0],c_1[:,1],marker = '+')
plt.scatter(c_0[:,0],c_0[:,1],marker = '^')
plt.scatter(c_2[:,0],c_2[:,1],marker = '*')
plt.scatter(c_3[:,0],c_3[:,1])
x = np.arange(-5,5)
y1 = -(W[0,0]*x + bias[0,0])/W[0,1]
y2 = -(W[1,0]*x + bias[0,1])/W[1,1]
y3 = -(W[2,0]*x + bias[0,2])/W[2,1]
y4 = -(W[3,0]*x + bias[0,3])/W[3,1]
plt.plot(x,y1,'b')
plt.plot(x,y2,'y')
plt.plot(x,y3,'g')
plt.plot(x,y4,'r')

def predict(x):
    y_hat = softmax(compute_y_hat(W,x,bias))
    #取one_hot编码中的最大值
    return np.argmax(y_hat,axis = 1)[:,np.newaxis]

np.sum(predict(test_data_X) == test_data_y)

9. 感知器

9.1. 感知器理论

感知器也是一个非常经典的机器学习线性模型的参数学习算法，他处理的是二分类问题：

给定大小为N的样本的训练集{(X1,y1),(X2,y2)……(Xn,yn)}，感知器的算法希望找到一组参数W，使得对于所有样本都有 y*W.T*X > 0

感知器也是一个由错误驱动的算法，因此我们也可以通过一个权重向量w，每次分错一个样本（x,y）时，可以得到yW.T*X < 0,其中y*x是小于0的，我们用y*x来更新权重：

感知器的学习过程：

损失函数：

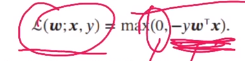
梯度：

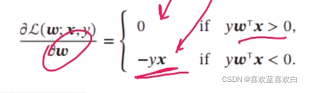
感知器的不足：

在数据集线性可分时，我们能找到一个超平面将两类数据分开，但并不能保证其泛化能力。
感知器对样本出现的顺序比较敏感，不同顺序找到的超平面往往也不一样。
如果训练集不是线性可分的，那就永远不会收敛。

9.2. 感知器（实战）

注意，感知器严格要求标签是1和-1。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)
Num = 100

# y = 1
x_1 = np.random.normal(6,1,size = (Num)) # 6附近的满足高斯分布的点
x_2 = np.random.normal(3,1,size = (Num)) # 3附近的反差为1的点
y = np.ones(Num)
c_1 = np.array([x_1,x_2,y]) #[x1,x2]是特征,y是样本的预测值。
c_1.shape

# y = -1
x_1 = np.random.normal(3,1,size = (Num)) # 6附近的满足高斯分布的点
x_2 = np.random.normal(6,1,size = (Num)) # 3附近的反差为1的点
y = np.ones(Num)*-1
c_0 = np.array([x_1,x_2,y]) #[x1,x2]是特征,y是样本的预测值。
c_0.shape

# 一般表头是特征，行是样本。
c_1 = c_1.T
c_0 = c_0.T

plt.scatter(c_1[:,0],c_1[:,1],marker = '+')
plt.scatter(c_0[:,0],c_0[:,1])

#混合
All_data = np.concatenate((c_1,c_0))
All_data.shape #(默认在行上拼接)

np.random.shuffle(All_data) #默认是在第一维度，也就是列上打乱。

np.random.shuffle(All_data)  #默认是在第一维度，也就是列上打乱。
train_data_X = All_data[:150, :2]
train_data_y = All_data[:150, -1].reshape(150,1)
test_data_X = All_data[150:, :2]
test_data_y = All_data[150:, -1].reshape(50,1)
train_data_X.shape, test_data_y.shape

W = np.zeros((2,1))
T = 10
k = 0
train_data = np.concatenate( (train_data_X,train_data_y) ,axis = 1 )

for t in range(T):
    np.random.shuffle(train_data)
    for i in range(len(train_data)):
        # 选取第 i 个样本
        pre = np.dot(W.T,( train_data[i][-1]*train_data[i][:2] ).reshape(2,1))[0,0]
        if pre <= 0:
            W = W + (train_data[i][-1]*train_data[i][:2]).reshape(2,1)

# y = w*x + w2 *x2
plt.scatter(c_1[:,0],c_1[:,1],marker = '+')
plt.scatter(c_0[:,0],c_0[:,1])
x = np.arange(10)
y = -(W[0]*x)/W[1]
plt.plot(x,y)

10. 用softmax回归进行MNIST数据集的手写数字识别（实战）

一个正确率为0.9009的W，也许是因为后面不小心多训练了几千次，导致有些偏执。

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import datasets

(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()

x_train.shape , y_train.shape,x_test.shape,y_test.shape

plt.imshow(x_train[0]/255.,cmap='gray')

# 把数据集形状变为： (60000,784)
x_train = x_train.reshape(-1,784)
x_train.shape

np.random.seed(0)
W = np.random.rand(784,10)
bias = np.random.rand(1,10)
W,bias.shape

#计算每个类别的预测值
def softmax(z):
    exp = np.exp(z - np.max(z,axis = 1).reshape(len(z),1))
    sum_exp = np.sum(exp,axis = 1,keepdims=True)
    return exp/sum_exp

#测试
tmp = np.arange(6).reshape(2,3)
softmax(tmp)

#给标签进行one-hot编码
def one_hot(temp):
    one_list = np.zeros((len(temp),len(np.unique(temp) )))
    one_list[np.arange(len(temp)) , temp.astype(np.int).T] = 1
    return one_list

#测试
one_hot(y_train)

#就算y_hat
def compute_y_hat(W,X,b):
    return np.dot(X,W) + b

# x_train.shape,W.shape,bias.shape
compute_y_hat(W,x_train,bias)

# 定义损失函数
def cross_entropy(y,y_hat):
    return -(1/len(y))*np.sum(np.nan_to_num(y*np.log(y_hat + 1e-9)))
# 测试

#定义超参数和其他参数：
Num = 100
lr = 0.001
loss_list = []
one_hot(y_train).shape,compute_y_hat(W,x_train,bias).shape

for t in range(Num):
    X = x_train
    y = one_hot(y_train)
    y_hat = compute_y_hat(W,X,bias)
    #讲y_hat转换为概率
    y_hat = softmax(y_hat)
    loss = cross_entropy(y,y_hat)
    loss_list.append(loss)
    # 计算梯度
    grad_w = (1/len(X))*np.dot(X.T,(y_hat - y))
    grad_b = (1/len(X))*np.sum(y_hat - y)
    #更新参数
    W = W - lr*grad_w
    bias = bias - lr*grad_b
    #输出
    if t%30 == 1:
        print("i: %d,loss : %f"%(t,loss))

W

plt.plot(loss_list)

def predict(x):
    y_hat = softmax(compute_y_hat(W,x,bias))
    #取one_hot编码中的最大值
    return np.argmax(y_hat,axis = 1)[:,np.newaxis]

x_test = x_test.reshape(-1,784)

pre = predict(x_test)
np.sum(pre.T == y_test)/len(y_test)