红黑树，算法导论

RB-Tree

本文将理解红黑树的性质，红黑树的插入、删除操作的源码及时间复杂度分析。

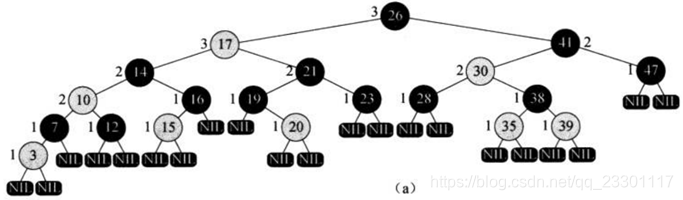
性质

1. 所有结点只有红、黑两色
2. 根结点是黑色
3. 任意节点到叶子结点的所有路径中还有的黑色结点的个数（黑高（hb(x)）相同
4. 叶子结点（nil）都为黑色
5. 红色结点的孩子结点一定是黑色

左旋

左右旋转结点是红黑树的插入和删除的基础操作。下面将给出左旋操作，右旋操作类似。

LEFT-ROTATE(T, x)
	y = x.left
	if x.p == T.nil
		T.root = y
	else if x == x.p.left
		x.p.left = y
	else 
		x.p.right = y
	y.p = x.p
	if y.left != nil
		y.left.p = x
	x.right = y.left
	x.p = y
	y.left = x

左旋的时间复杂度为：O(1)

插入

RB-INSERT(T, z)
	y = T.nil
	x = T.root
	while x != T.nil
		y = x
		if y.key < z.key
			x = x.right
		else 
			x = x.left
	z.p = y
	if y == T.nil
		T.root = z
	else if y.key < z.key
		y.right = z
	else 
		y.left = z
	z.left = T.nil
	z.right = T.nil
	z.color = RED
	RB-INSERT-FIXUP(T, z)

RB-INSERT-FIXUP(T, z)
	while z.p.color == RED
		if z.p == z.p.p.left
			y = z.p.p.right
			if y.color == RED              
				y.color = BLACK            //case 1  叔父节点为红色
				z.p.color = BLACK          //case 1   
				z.p.p.color = RED          //case 1
				z = z.p.p                  //case 1
			else if z == z.p.right 
				z = z.p                    //case 2  叔父节点y为黑色且z为右孩子
				LEFT-ROTATE(T, z)          //case 2
			z.p.color = BLACK              //case 3  叔父节点y为黑色且z为左孩子
			z.p.p.color = RED              //case 3
			RIGHT-ROTATE(T, z.p.p)         //case 3
		else same as then clause with "right" and "left" exchanged
	T.root.color = BLACK

分析
RB-INSERT：由于一棵树有n个节点的红黑树的高度为O(lgn) ，因此RB-INSERT的时间复杂度为O(lgn)，最后一行RB-INSERT(T, z)中，O(lgn)，最多旋转两次就结束。

删除

RB-TRANSPLANT(T, u, v)
	if u.p == T.nil
		T.root == v
	else if u == u.p.left
		u.p.left = v
	else u.p.right = v
v.p = u.p

RB-DELETE(T, z)
	y = z
	y-original-color = y.color
	if z.left == T.nil
		x = z.right
		RB-TRANSPLANT(T, z, z.right)
	else if z.right = T.nil
		x = z.left
		RB-TRANSPLANT(T, z, z.left)
	else y == TREE-MINMUM(z.right)
		y-original-color = y.color
		x = y.right
		if y.p == z
			x.p = y
		else RB-TRANSPLANT(T, y, y.right)
			y.right = z.right
			y.right.p = y
		RB-TRANSPLANT(T, z, y)
		y.left = z.left
		y.left.p = y
		y.color = z.color
	if y-original-color == BLACK
		RB-DELETE-FIXUP(T, x)

RB-DELETE-FIXUP(T, x)
	while x != T.root && x.color == BLACK
		if x == x.p.left
			w = x.p.right
			if w.color == RED  
				w.color = BLACK                                //case 1 x的兄弟节点为红色
 				x.p.color = RED                                //case 1
				LEFT-ROTATE(T, x.p)                            //case 1
				w = x.p.right                                  //case 1
			if w.left.color == BLACK && w.right.color == BLACK    
				w.color = BLACK                                //case 2 x的兄弟节点w为黑色且它的左孩子为黑色右孩子也为黑色
				x = x.p									       //case 2
			else if w.right.color == BLACK
					w.left.color = BLACK                       //case 3 x的兄弟节点w为黑色，且它的左孩子为红色，右孩子为黑色
					w.color = RED                              //case 3
					RIGHT-ROTATE(t, w)                         //case 3
					w = x.right                                //case 3
				w.color = x.p.color                            //case 4 x的兄弟节点w为黑色，且它的右孩子为红色
				w.right.color = BLACK                          //case 4
				x.p.color = BLACK                              //case 4
				LEFT-ROTATE(T, x.p)                            //case 4
			x = T.root			
		else (same as then clause with "right" and "left" exchanged)
x.color == BLACK

分析
RB-DELDET的时间复杂度分为两个部分一个是删除节点z，另一个是对红黑树进行重新着色。删除节点z需要O(lgn)的时间复杂度，重新着色需要lg(n)的时间复杂度（主要是case 2）。所以最后的时间复杂度为O(lgn)

参考

《算法导论》