一、动态规划解决什么问题
将复杂问题分解为子问题,子问题会多次重复出现,存储子问题结果以避免重复计算的优化方法。
二、从斐波那契额数列开始
斐波那契数列是指这样一个数列:0,1,1,2,3,5,8,13,21,34,55,89……这个数列从第3项开始 ,每一项都等于前两项之和。
可以记作:
F(0) = 0
F(1) = 1
F(n) = F(n-1) + F(n-2)(n ≥ 2)
需求:写一个函数 Fib(n) 返回第 n 个斐波那契数。
1.1 暴力计算
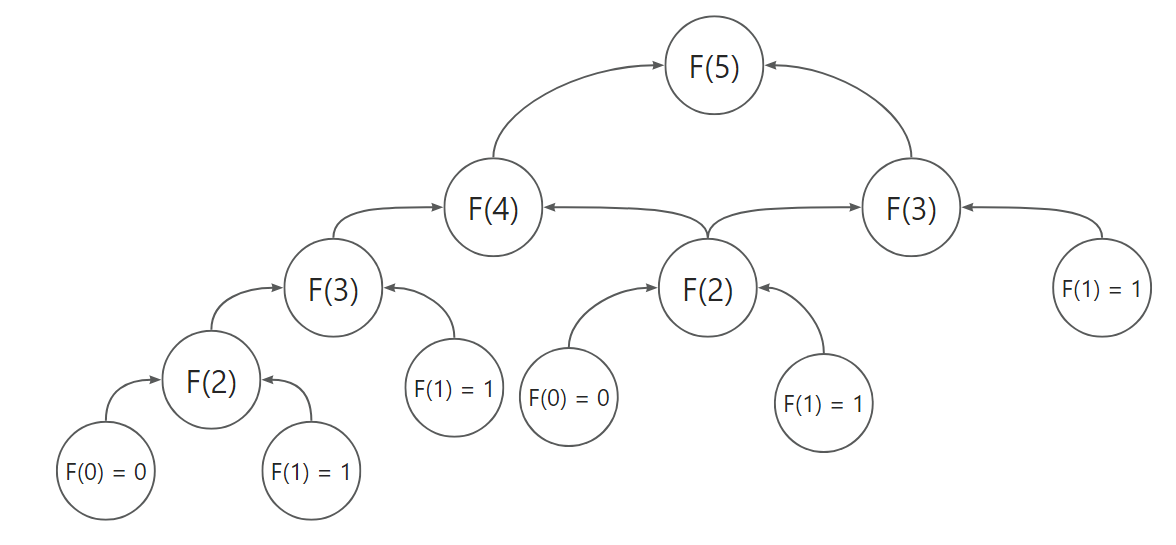
比如算F(5)需要计算F(4...0)。
算F(4)的时候计算F(3...0)。
算F(3)的时候计算F(2...0)。
算F(2)的时候需要计算F(1)+F(0).
其中有大量的过程被重复了,比如算F(5)的所有过程中F(3)就同时被F(5)和F(4)需求了。
下面是暴力算法,完全按照斐波那契的计算公式来写:
using System;
class Program
{
static int FibNaive(int n)
{
if (n == 0) return 0;
if (n == 1) return 1;
// 完全照公式写:F(n) = F(n-1) + F(n-2)
return FibNaive(n - 1) + FibNaive(n - 2);
}
static void Main()
{
Console.WriteLine(FibNaive(10));
}
}
1.2 优化
我们会发现Fib(0)、Fib(1)...Fib(n-1)每一个结果都会被多次的使用,如果我们将Fib(x)的计算结果存储在一个数据结构中,如果有就从这个数据结构中拿,就会减少调用Fib。比如:
using System;
class Program
{
static int[] memo;
static int FibMemo(int n)
{
if (n == 0) return 0;
if (n == 1) return 1;
if (memo[n] != -1) // 之前算过了,直接用
return memo[n];
memo[n] = FibMemo(n - 1) + FibMemo(n - 2);
return memo[n];
}
static void Main()
{
int n = 40;
memo = new int[n + 1];
// 用 -1 表示“还没计算过”
for (int i = 0; i <= n; i++)
memo[i] = -1;
Console.WriteLine(FibMemo(n));
}
}
我们从参数N开始递归一直递归到N=2,称之为从上到下。过程中我们使用了一个int[] memo数组来存储Fib(x)的结果,如果再次遇到就直接从数组拿。即memo[i] 表示 F(i) 的值。
当然我们也可以从下到上,即从下标2开始计算到N:
using System;
class Program
{
static long FibDP(int n)
{
if (n == 0) return 0;
if (n == 1) return 1;
long[] dp = new long[n + 1];
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++)
{
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
static void Main()
{
int n = 50;
Console.WriteLine(FibDP(n));
}
}
我们发现,当long[] dp填满的时候,dp[n]就是结果。
1.3 思想总结
DP能解决的问题都有这些基本特征:
-
大问题可以拆成小问题(最优子结构)
-
小问题会反复出现(子问题重叠)
-
无后效性,或称为【有序无环图】。
如果我们每次都“重新算一遍小问题”,就会很浪费(典型:斐波那契数)。
DP 的核心就是:小问题的答案算一次就存起来,之后直接用。
重点说一下无后效性,这个词很抽象,有序无环图更好理解:
通过箭头我们就可以直观的感受到【有序】。

如果有环呢?比如下面:
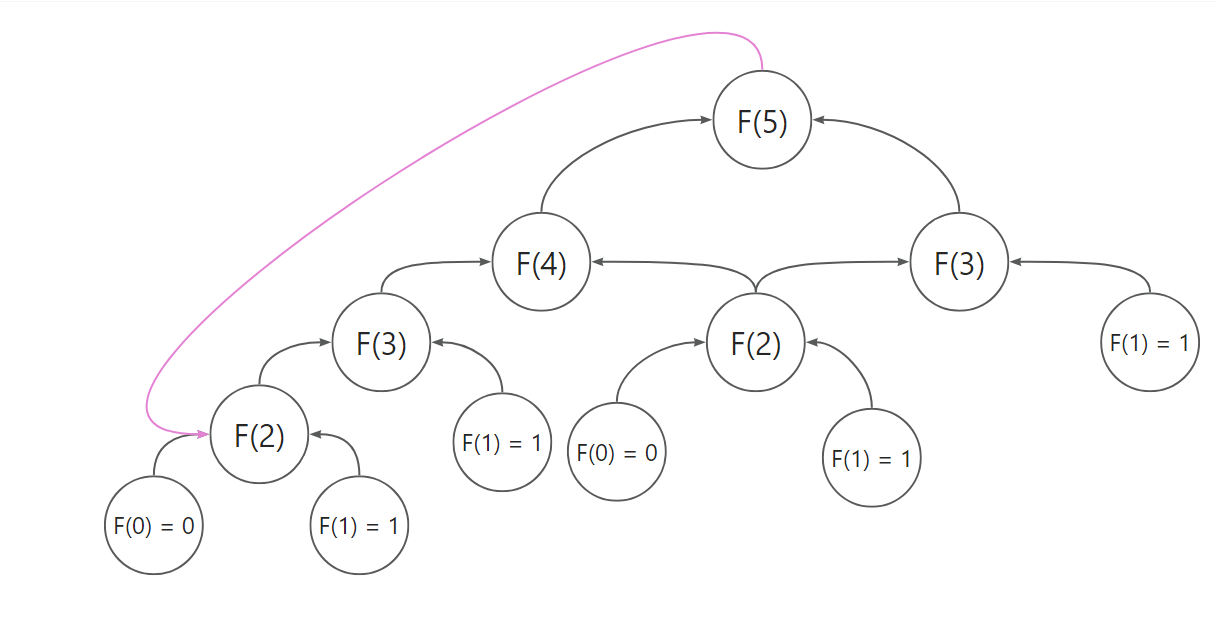
F(2) = F(1)+F(0)+F(5), 那么我们发现F(2)、F(3)、F(4)、F(5)成环了,问题将无法求解,所以需要无环。
无后效性是动态规划能成立的基础。如果一个问题存在环路(如动态依赖关系),那就无法使用动态规划来优化,因为子问题的解无法按顺序进行计算
三、再抽象一点
三个词:状态、状态转移、边界。
3.1 边界
边界最好理解,比如斐波那契数列中,F(0)和F(1)就是边界。
3.2 状态
比如斐波那契数列中每个节点都是一个状态。
状态是子问题的集合,就像斐波那契数列中F(5)此时的状态就是子问题F(4...0)子问题的集合。
3.3 状态转移
状态转移也好理解,比如计算F(5) = F(4) + F(3)。F(5)的状态来自于F(4)状态结果和F(3)状态结果的和,这个过程就是状态转移。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








