MCMC采样算法理解

MCMC采样算法

完整的MCMC采样算法已经有很多博主发布了，这里就不再重复了。主要想分享一下在看其他博主写的MCMC采样算法时，不太理解的地方。

MCMC采样关键问题在于如何构建转移矩阵，使得平稳分布恰好是p(x)。主要使用细致平稳条件。

细致平稳条件

如果非周期马氏链的转移矩阵P和分布π(x)满足：
π(i)Pij=π(j)Pji for all i,j
则π(x)是马尔可夫链的平稳分布，上式称为细致平稳条件。

马氏链的一个例子：
社会学家经常把人按其经济状况分成3类：下层(lower-class)、中层(middle-class)、上层(upper-class)，我们用1,2,3 分别代表这三个阶层。社会学家们发现决定一个人的收入阶层的最重要的因素就是其父母的收入阶层。如果一个人的收入属于下层类别，那么他的孩子属于下层收入的概率是 0.65, 属于中层收入的概率是 0.28, 属于上层收入的概率是 0.07。事实上，从父代到子代，收入阶层的变化的转移概率如下

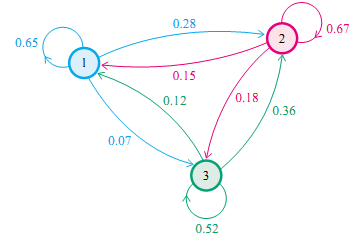
假设初始概率分布为π0=[0.21,0.68,0.11]，则我们可以计算前n代人的分布状况如下：

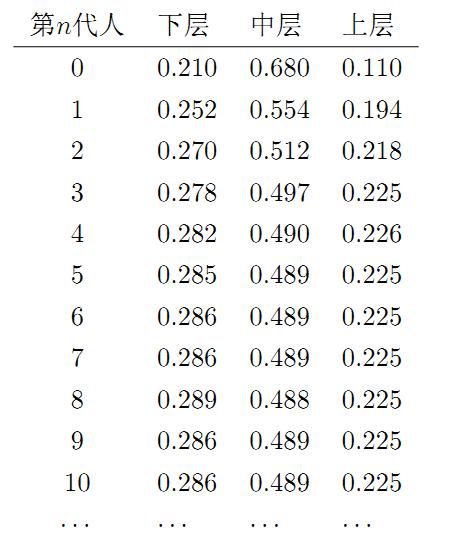
从第7代人开始，这个分布开始稳定不变。

回到细致平稳分布，当达到马氏链的平稳分布的时候，π=(0.286，0.489，0.225)，由细致平稳可知满足π